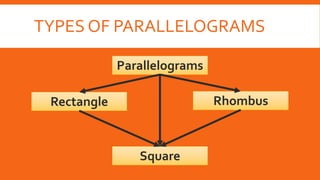
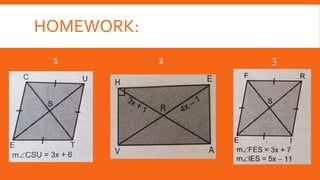
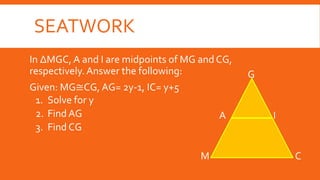
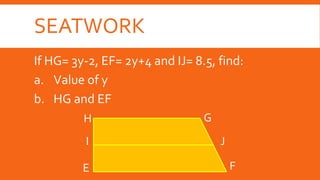
This document defines and describes types of quadrilaterals including parallelograms, trapezoids, kites, rectangles, rhombuses, and squares. It provides properties and theorems for each shape and examples to solve problems involving midlines, midsegments, isosceles trapezoids, and kites. Seatwork and homework problems are also presented.

1. QUADRILATERALS
POLYGONWITH 4 SIDES

2. TYPES OF QUADRILATERALS
1. Parallelogram- quadrilateral with 2 pairs of
parallel sides
2.Trapezoid- quadrilateral with 1 pair of
parallel sides
3. Kite- quadrilateral with no pair of parallel
sides

3. PARALLELOGRAMS
 Quadrilateral with 2 pairs of parallel sides
 Parallel- lines that do not meet
 Quadrilateral MATH is a parallelogram
M A
S
H T

4. PROPERTIES OF PARALLELOGRAMS
SIDES
1. Opposite sides are congruent.
ANGLES
2. Opposite angles are congruent.
3. Consecutive angles are supplementary.
DIAGONALS
4. Diagonals bisect each other.
5. Diagonal forms two congruent triangles.

5. TYPES OF PARALLELOGRAMS
Parallelograms
Square
Rhombus
Rectangle

6. THEOREMS ON RECTANGLE
1. All angles are right angles.
2. Diagonals are congruent.
Given: QuadrilateralCARE is a rectangle.
C A
S
E R

7. THEOREMS ON RHOMBUS
Rhombus- parallelogram whose sides are congruent
1. Diagonals are perpendicular
2. Diagonals bisect opposite angles.
Given: Quadrilateral HEAR is a rhombus.
H E
T
R A

8. SQUARE
-Sides are congruent, therefore it
is a rhombus.
-A type of parallelogram whose
diagonals are perpendicular and
congruent.

9. WHAT MAKES THE SQUARE
EXTRA SPECIAL?

10. TYPES OF PARALLELOGRAMS
Parallelograms
Square
Rhombus
Rectangle

11. SEATWORK:
I. Name all quadrilaterals using the legend below with the given
properties:
P- parallelogram Re- rectangle Rh- rhombus and S- square
1. Diagonals are congruent.
2. Diagonals bisect each other.
3. Diagonals are perpendicular.
4. One pair of opposite sides are parallel.
5. All sides are congruent.

12. SEATWORK:
II.Write always true, sometimes true or never true.
1. A square is a rectangle.
2. A rhombus is a square.
3. A parallelogram is a square.
4. A rectangle is a rhombus.
5. A quadrilateral is a parallelogram.

13. HOMEWORK:
1 2 3

14. MIDLINE
A line joining two midpoints of the
sides of a triangle.
Parallel to the base
Half the measure of the base
ML=
𝐵
2

15. EXAMPLE
In ∆MGC, A and I are midpoints of MG and CG,
respectively.Answer the following:
1. Given:AI= 10.5, find MC.
2. Given: CG= 32, find GI.
3. Given:AG= 7, CI=8, find MG+CG.
4. Given: AI= 3x-2 and MC= 9x-13,
1. Solve for x
2. Find AI
3. Find MC
M C
I
G
A

16. SEATWORK
In ∆MGC, A and I are midpoints of MG and CG,
respectively.Answer the following:
Given: MG≅CG, AG= 2y-1, IC= y+5
1. Solve for y
2. Find AG
3. Find CG
M C
I
G
A

17. MIDSEGMENT
A line joining two midpoints of the sides
of a trapezoid
Also known as median
Parallel to the bases
Half the measure of the bases
MS=
𝑏1+𝑏2
2

18. EXAMPLE
1. If IJ= x, HG= 8 and EF= 12, find x.
2.If HG= x, IJ= 16 and EF= 22, find x.
H
F
J
G
I
E

19. SEATWORK
If HG= 3y-2, EF= 2y+4 and IJ= 8.5, find:
a. Value of y
b. HG and EF
H
F
J
G
I
E

20. ISOSCELESTRAPEZOID
1.Base angles are congruent
2.Opposite angles are supplementary
3.Diagonals are congruent

21. EXAMPLE:
Consider quadrilateral MATH is a trapezoid, answer the following
questions:
1. If ∠𝐻𝑀𝐴= 115°, find ∠𝑇𝐴M.
2. If ∠𝑀𝐻𝑇 = 3𝑥 + 10 𝑎𝑛𝑑 ∠𝑀𝐴𝑇 = 2𝑥 − 5, find the measure
of the two angles. M A
T H

22. SEATWORK:
Using the same given as the example, if AH=
4y-3 and MT= 2y+5, find:
a.The property used to solve the problem
b.Value of y
c. Length of AH

23. KITE
A quadrilateral whose pair of adjacent
sides are equal
Properties:
1. Diagonals are perpendicular
2. Area of a kite is half the product of its
diagonals

24. EXAMPLE
Quadrilateral PLAY is a kite. P
1. PA= 12, LY= 6. Find the area. L
2. Area= 135, LY= 9. Find PA. S
3. If PL= 6, find PY. Y
4. Find m∠𝑃𝑆𝐿.
5. If m∠LAS = 30° , find m∠𝐴𝐿𝑆. A

25. QUIZ:
A quadrilateral POST is an isosceles trapezoid with OS ∥ PT. ER is a
median.
1-2. Draw the figure and label its parts.
3-5. If OS= 3x-2, PT= 2x+10 and ER= 14, how long is OS and PT?
6-7. If angle P= 2x+5 and angle O= 3x-10, what is angleT?
A quadrilateral LIKE is a kite where LI≅IK and LE ≅KE.
8-9. Draw the figure and label its parts.
10-11. If LE is twice LI and the perimeter is 21, find LE.
12-15. If IE= x-1 and LK= x+2, how long is IE and LK if the area is 44?