The document discusses coordinate proofs involving quadrilaterals. It provides examples of determining if quadrilaterals are congruent or similar by analyzing corresponding sides and angles. It also covers properties of parallelograms, rectangles, and rhombuses, such as having opposite sides that are congruent and opposite angles that are congruent. Examples are given of supplying missing coordinates to complete parallelograms and rectangles.

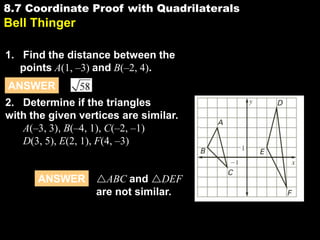
1. 8.7 Coordinate Proof with Quadrilaterals
8.7
Bell Thinger
1. Find the distance between the
points A(1, –3) and B(–2, 4).
ANSWER
2. Determine if the triangles
with the given vertices are similar.
A(–3, 3), B(–4, 1), C(–2, –1)
D(3, 5), E(2, 1), F(4, –3)
ANSWER
ABC and DEF
are not similar.

2. 8.7
Example 1
Determine if the quadrilaterals with the given
vertices are congruent.
O(0, 0), B(1, 3), C(3, 3), D(2, 0);
E(4, 0), F(5, 3), G(7, 3), H(6, 0)
SOLUTION
Graph the quadrilaterals. Show
that corresponding sides and
angles are congruent.
Use the Distance Formula.
OB = DC = EF = HG =
OD = BC = EH = FG = 2
Since both pairs of opposite sides in each quadrilateral
are congruent, OBCD and EFGH are parallelograms.

3. 8.7
Example 1
Opposite angles in a parallelogram are congruent, so
O
C and E
G.
and
are parallel, because
both have slope 3, and they are cut by transversal
.
So, O and E are corresponding angles, and
By substitution, C
G.
Similar reasoning can be used to show that
and D
H.
O
B
Because all corresponding sides and angles are
congruent, OBCD is congruent to EFGH.
E.
F

4. 8.7
Guided Practice
Find all side lengths of the quadrilaterals with the
given vertices. Then determine if the quadrilaterals are
congruent.
1. F(–4, 0), G(–3, 3), H(0, 3), J(–2, 0);
P(1, 0), Q(2, 3), R(6, 3), S(4, 0)
ANSWER
not congruent

5. 8.7
Guided Practice
Find all side lengths of the quadrilaterals with the
given vertices. Then determine if the quadrilaterals are
congruent.
2. A(–2, –2), B(–2, 2), C(2, 2), D(2, –2);
O(0, 0), X(0, 4), Y(4, 4), Z(4, 0)
ANSWER
AB = BC = CD = DA = OX = XY = YZ = ZO = 4;
all angles are right angles; congruent

6. 8.7
Example 2
Determine if the quadrilaterals with the given
vertices are similar.
O(0, 0), B(4, 4), C(8, 4), D(4, 0);
O(0, 0), E(2, 2), F(4, 2), G(2, 0)
SOLUTION
Graph the quadrilaterals. Find
the ratios of corresponding
side lengths.

7. 8.7
Example 2
Because OB = CD and BC = DO, OBCD is a parallelogram.
Because OE = FG and EF = GO, OEFG is a parallelogram.
Opposite angles in a parallelogram are congruent, so
O
F and O
C. Therefore, C
F.
Parallel lines
and
are cut by transversal
, so
B and FEO are corresponding angles, and B
FEO.

8. 8.7
Example 2
Likewise,
and
are parallel lines because both
have slope 1, and they are cut by transversal
, so D
and OGF are corresponding angles, and D
OGF .
Because corresponding side lengths are proportional
and corresponding angles are congruent, OBCD is
similar to OEFG.

9. 8.7
Example 3
Show that the glass pane in the center
is a rhombus that is not a square.
SOLUTION
Use the Distance Formula. Each
side of ABCD has length
units.
So, the quadrilateral is a rhombus.
The slope of
of
is –3.
is 3 and the slope
Because the product of these slopes is not –1, the
segments do not form a right angle. The pane is a
rhombus, but it is not a square.

10. 8.7
Example 4
Without introducing any new
variables, supply the missing
coordinates for K so that OJKL
is a parallelogram.
SOLUTION
Choose coordinates so that opposite sides of the
quadrilateral are parallel.
must be horizontal to be parallel to
y-coordinate of K is c.
, so the

11. 8.7
Example 4
To find the x-coordinate of K, write expressions for the
slopes of
and
. Use x for the x-coordinate of K.
The slopes are equal, so
a, and x = a + b.
Point K has coordinates (a + b, c).
. Therefore, b = x –

12. 8.7
Example 5
Prove that the diagonals of a parallelogram bisect each
other.
SOLUTION
STEP 1 Place a parallelogram with coordinates
as in Example 4. Draw the diagonals.

13. 8.7
Example 5
STEP 2 Find the midpoints of the diagonals.
The midpoints are the same. So, the diagonals bisect
each other.

14. 8.7
Guided Practice
6. Write a coordinate proof that the diagonals of a
rectangle are congruent.
ANSWER
Place rectangle OPQR so that it is in the first
quadrant, with points O(0, 0), P(0, b), Q(c, b), and R(c, 0).
Use the Distance Formula.
So, the diagonals of a rectangle are congruent.

15. Exit
8.7 Slip
1. Find the side lengths of the quadrilaterals with
the given vertices. Then determine if the
quadrilaterals are congruent.
J(1, 1), K(2, 4), L(5, 4), M(4, 1);
N(–1, –3), O(0, 0), P(4, 0), Q(3, –3)
ANSWER
JK = LM = NO = PQ =
KL = JM = 3 but OP = NQ = 4;
not congruent

16. Exit
8.7 Slip
2. Find the side lengths of the quadrilaterals with
the given vertices. Then determine if the
quadrilaterals are similar.
R(–2, 3), S(–2, 1), T(–4, 1), U(–4, 3);
V(5, 2), W(5, –2), X(1, –2), Y(1, 2)
ANSWER
RS = ST = TU = RU = 2,
VW = WX = XY = VY = 4;
corresponding sides are proportional
and corresponding angles are ; similar

17. Exit
8.7 Slip
3. Without introducing any new variables, supply
the missing coordinates for G so that EFGH is a
rectangle.
ANSWER
(d, c)

18. 8.7
Pg
#