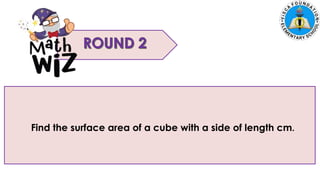
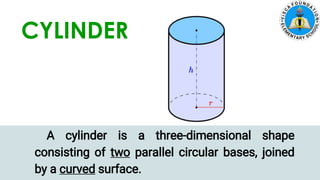
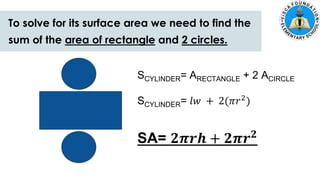
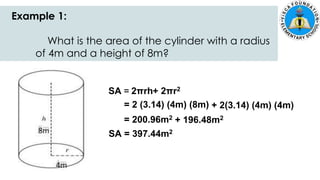
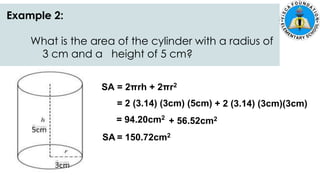
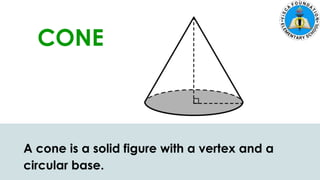
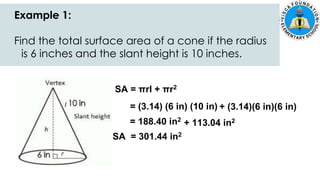
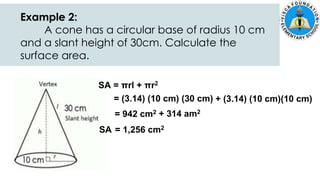
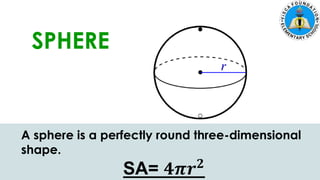
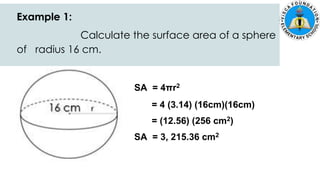
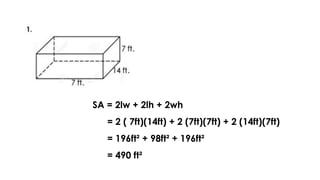
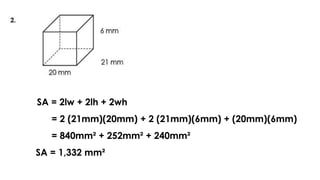
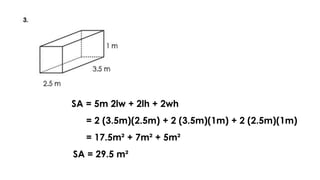
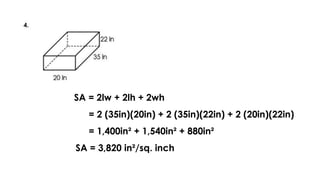
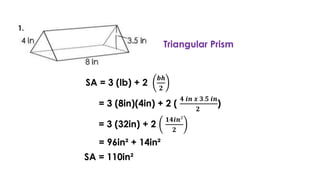
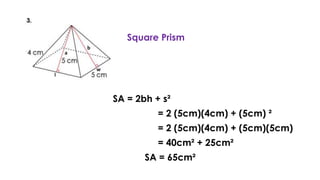
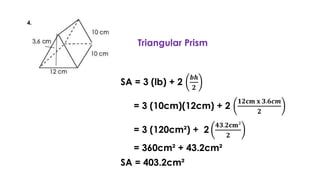
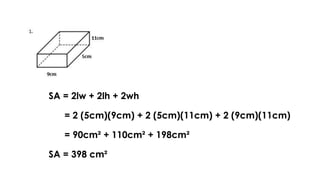
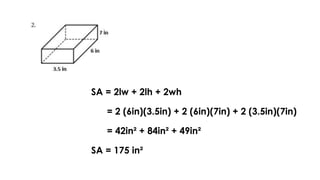
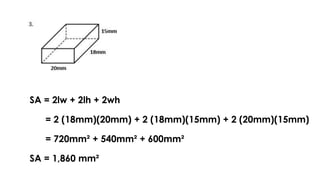
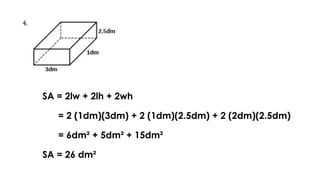
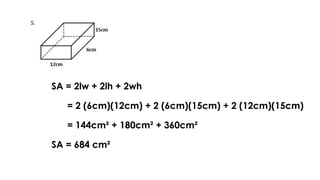
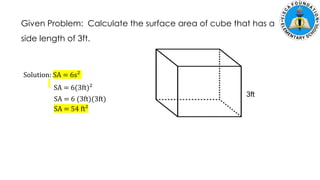
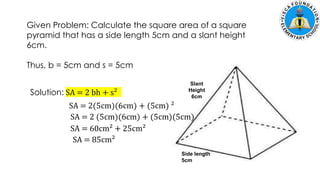
The document discusses calculating the surface areas of various geometric solids. It provides formulas for finding the surface areas of prisms, cubes, pyramids, cylinders, cones, and spheres. Examples are given for calculating surface areas of specific shapes using the appropriate formulas and given measurements of lengths, widths, heights, radii, etc. The objectives are to find surface areas of solid figures and solve word problems involving surface areas of solid figures.

2. The surface area is the area that describes
the material that will be used to cover a
geometric solid. When we determine the
surface areas of a geometric solid, we take
the sum of the area for each geometric form
within the solid.

3. OBJECTIVES
 Find the surface area of solid figures
 Solve word problems involving solid figures

5. Surface Area-is the sum of the areas of all the faces of
the three-dimensional figure - sum of lateral faces and
the bases SA = L.A + B
Prism- is a 3-dimensional shape with two identical
shapes facing each other. These identical shapes are
called “bases”. The bases can be triangular,
rectangular, square or any other polygon.

6. Triangular Prism
Triangle prism has 3 rectangular faces and 2 triangular
faces.
To get its surface area, find the area of its three
rectangular faces and add it to the area of its Two
Triangular faces.
Formula: SA = 3 (lb) + 2 (
𝑏ℎ
2
)
Where : l = length b = base h = height

7. Given Problem: Calculate the surface area of a
Triangular prism with a side length 12 cm, base 8cm, and
height 3cm.
12 cm
8 cm
3 cm
Solution: SA = 3 (lb) + 2 (
𝑏ℎ
2
)
SA= 3[ (12cm)(8cm) ] + 2(
(8𝑐𝑚)(3𝑐𝑚)
2
)
SA= 3(96 sq. cm) + 2(
24 𝑠𝑞.𝑐𝑚
2
)
SA= 288 sq. cm + 24 sq. cm
SA= 312 sq. cm

8. Cube/Square Prism
Cube/Square prism has 6 squares faces if we unfold this solid
figure
To get surface area, we should find the area of one of the
squares and multiply it by 6 since there are 6 squares faces in
a cube.
The formula for cube/square prism is SA = 6s²
Where = S = side length

9. Given Problem: Calculate the surface area of cube that has a
side length of 3ft.
Solution: SA = 6s²
3ft
SA = 6(3ft)²
SA = 6 (3ft)(3ft)
SA = 54 ft²

10. Rectangular Prism
In finding surface area for all rectangular prisms (including
cubes) involves both addition and multiplication. You must
know the width, length and height of the prism before you can
apply this formula: SA = 2lw + 2lh + 2wh or SA = 2(lw + lh + wh)
A rectangular prism has a rectangular and/or square faces.

11. Given Problem: Find the surface of a rectangular prism
with width 6cm, h= 12cm, and length 5cm.
Solution: SA = 2lw + 2lh + 2wh
SA= 60cm² + 120cm² + 144cm²
SA = 2(5cm)(6cm) + 2(5cm)(12cm)+ 2(6cm)(12cm)
SA = 324cm²

12. Square Pyramid
Square pyramid has 1 square face and triangular faces.
To get its surface area, find the area of the square base and add it to
the area of the 4 triangular faces
Formula: SA = 2 bh + s²
Where b = base
h = slant height
s = side length of the square
Take Note: The side length of the square base is always the
same with the length of the base of the triangle.

13. Given Problem: Calculate the square area of a square
pyramid that has a side length 5cm and a slant height
6cm.
Thus, b = 5cm and s = 5cm
Solution: SA = 2 bh + s²
Slant
Height
6cm
Side length
5cm
SA = 2(5cm)(6cm) + (5cm) ²
SA = 2 (5cm)(6cm) + (5cm)(5cm)
SA = 60cm² + 25cm²
SA = 85cm²

14. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
Mechanics of the game:
1. Students has to prepare pen and paper
2. The teacher will flash the word problems on the screen.
3. The students will solve the problem and the first one to finish will,
recite the word;
“I am (name), a math wizard.”
4. There will be 30 seconds time limit.
5. The winner will be given two points.
(The points will be added to the score in Assessment)

15. Rachel parents brought him a wooden toy in shape
triangular prism with length of 14cm base 3cm, and
height 4cm. Rachel wants to cover it with stickers. How
many square units of stickers will she need to cover the
surface of the wooden toy?

17. SA = 3(lb) + 2
𝒃𝒉
𝟐
= 3 [(14cm)(3cm)] + 2
(𝟑𝒄𝒎)(𝟒𝒄𝒎)
𝟐
= 3 (42cm²) + 12cm²
= 126cm² + 12cm²
= 138cm²

18. Find the surface area of a cube with a side of length cm.

20. SA = 6s²
= 6(6cm) ²
= 6(6cm) (6cm)
= 6 x 36cm²
SA= 216cm²

21. What is the surface area of a square pyramid
with a perpendicular height of 8m and base
length of 12m?

23. SA = 2bh+s²
= 2(12m x 8m) + (12m) ²
= 2 (12m x 8m) + (12m)(12m)
= 192m² + 144m²
SA = 336m²

24. You are building a new, larger rectangular aquarium
for your pet fish. You want the aquarium to be 4 feet
long, 1 foot wide, and 3 feet tall. How many square feet
of glass do you need to make the aquarium (if glass i s
used on all six sides)?

26. SA = 2lw + 2lh + 2wh
= 2(4ft x 1ft) + 2 (4ft x 3ft) + 2 (1ft x 3ft)
= 8sq.ft + 24sq.ft + 6sq.ft
= 38 sq.ft

27. CYLINDER
A cylinder is a three-dimensional shape
consisting of two parallel circular bases, joined
by a curved surface.

28. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
To solve for its surface area we need to find the
sum of the area of rectangle and 2 circles.
SCYLINDER= ARECTANGLE + 2 ACIRCLE
SCYLINDER= 𝑙𝑤 + 2(𝜋𝑟2
)
SA= 𝟐𝝅𝒓𝒉 + 𝟐𝝅𝒓𝟐

29. Example 1:
What is the area of the cylinder with a radius
of 4m and a height of 8m?
SA = 2πrh+ 2πr2
= 2 (3.14) (4m) (8m) + 2(3.14) (4m) (4m)
= 200.96m2 + 196.48m2
SA = 397.44m2

30. Example 2:
What is the area of the cylinder with a radius of
3 cm and a height of 5 cm?
SA = 2πrh + 2πr2
= 2 (3.14) (3cm) (5cm) + 2 (3.14) (3cm)(3cm)
= 94.20cm2
+ 56.52cm2
SA = 150.72cm2

31. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
CONE
A cone is a solid figure with a vertex and a
circular base.

32. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
To solve the surface area of the cone, we need to
find the sum of the lateral (side) and circular base
SA= 𝝅 𝒓𝒍 + 𝝅𝒓𝟐

33. SA = πrl + πr2
= (3.14) (6 in) (10 in) + (3.14)(6 in)(6 in)
= 188.40 in2
+ 113.04 in2
SA = 301.44 in2
Example 1:
Find the total surface area of a cone if the radius
is 6 inches and the slant height is 10 inches.

34. SA = πrl + πr2
= (3.14) (10 cm) (30 cm) + (3.14) (10 cm)(10 cm)
= 942 cm2 + 314 am2
SA = 1,256 cm2
Example 2:
A cone has a circular base of radius 10 cm
and a slant height of 30cm. Calculate the
surface area.

35. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
SPHERE
A sphere is a perfectly round three-dimensional
shape.
SA= 𝟒𝝅𝒓𝟐

36. Example 1:
Calculate the surface area of a sphere
of radius 16 cm.
SA = 4πr2
= 4 (3.14) (16cm)(16cm)
= (12.56) (256 cm2)
SA = 3, 215.36 cm2

37. Example 2:
Mang Cardo’s goat is tied to a tree
with a 9-meter rope. Around how many square
meters of grazing area do the goat have?
SA = 4πr2
= 4 (3.14) (9 m)(9 m)
= (12.56) (81 m2)
SA = 1, 017.36m2

38. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
Mechanics of the game:
1. Students has to prepare pen and paper
2. The teacher will flash the word problems on the screen.
3. The students will solve the problem and the first one to finish will,
recite the word;
“I am (name), a math wizard.”
4. There will be 30 seconds time limit.
5. The winner will be given two points.
(The points will be added to the score in Assessment)

39. Jake bought a canned Monster energy drink that has
Radius of 4 inches and a height of 8 inches.
Find the total surface area of the can.

41. SA = 2πrh + 2πr2
= 2 (3.14) (4 in ) (8 in ) + 2(3.14) (4m)(4m)
= 200.96 in2 + 100.48 in2
SA = 301.44m2

42. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
Find the total surface area of Annie’s party hat with a
radius 5 inches and slant height 10 inches.
Find the total surface area of the party hat.

44. SA = πrl + πr2
= (3.14) (5 in) (10 in) + (3.14) (5 in) (5 in)
= 157 in2 + 78.50 in2
SA = 235.50 in2

45. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
Calculate the surface area of a globe of radius
3.2 m

47. SA= 4π r2
= 4π (3.2)2
= 4 × 3.14 × 3.2 × 3.2
= 128.61 m2

48. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
LET’S TRY!
Application
Solve On Your Own A. Find the surface area of each cube
Surface Area.
1. Side = 2 cm ______________
2. Side = 6 ft. ______________
3. Side = 4 in ______________
4. Side = 7 yd. ______________
5. Side = 12 m ______________
6. Side = 9 ft. ______________
7. Side = 25mm _____________
8. Side = 19 in ______________

49. 1. SA = 6s²
= 6 (2 cm) (2 cm)
= 6 (4 cm2)
= 24 cm2
2. SA = 6s²
= 6 (6 ft.) (6 ft.)
= 6 (36 ft2)
= 216 ft.2
3.
4.
SA = 6s²
SA = 6s²
= 6 (4 in) (4 in)
= 6 (16 in2)
= 96 in2
= 6 (7 yd.) (7 yd.)
= 6 (49 yd.2)
= 294 yd.2

50. 5. SA = 6s²
= 6 (12 m) (12 m)
= 6 (144 m2)
= 864 m2
6. SA = 6s²
= 6 (9 ft.) (9 ft.)
= 6 (81 ft.2)
= 486 ft.2
7. SA = 6s²
= 6 (25 mm) (25 mm)
= 6 (625 mm2)
= 3, 750 mm2
8.
SA = 6s²
= 6 (19 in) (19 in)
= 6 (361 in2)
= 2, 166 in2

51. SA = 2lw + 2lh + 2wh
= 2 ( 7ft)(14ft) + 2 (7ft)(7ft) + 2 (14ft)(7ft)
= 196ft² + 98ft² + 196ft²
= 490 ft²

52. SA = 2lw + 2lh + 2wh
= 2 (21mm)(20mm) + 2 (21mm)(6mm) + (20mm)(6mm)
= 840mm² + 252mm² + 240mm²
SA = 1,332 mm²

53. SA = 5m 2lw + 2lh + 2wh
= 2 (3.5m)(2.5m) + 2 (3.5m)(1m) + 2 (2.5m)(1m)
= 17.5m² + 7m² + 5m²
SA = 29.5 m²

54. SA = 2lw + 2lh + 2wh
= 2 (35in)(20in) + 2 (35in)(22in) + 2 (20in)(22in)
= 1,400in² + 1,540in² + 880in²
SA = 3,820 in²/sq. inch

55. Triangular Prism
SA = 3 (lb) + 2
𝒃𝒉
𝟐
= 3 (8in)(4in) + 2 (
𝟒 𝒊𝒏 𝒙 𝟑.𝟓 𝒊𝒏
𝟐
)
= 3 (32in) + 2
𝟏𝟒𝒊𝒏²
𝟐
= 96in² + 14in²
SA = 110in²

56. Rectangular Prism
SA = 2lw + 2lh + 2wh
= 2 (79 ft.)(13 ft.) + 2 (79 ft.)(3 ft.) + 2 (13 ft.)(3 ft.)
= 2,054 ft² + 474 ft² + 78 ft²
SA = 2,606 ft²

57. Square Prism
SA = 2bh + s²
= 2 (5cm)(4cm) + (5cm) ²
= 2 (5cm)(4cm) + (5cm)(5cm)
= 40cm² + 25cm²
SA = 65cm²

58. Triangular Prism
SA = 3 (lb) + 2
𝒃𝒉
𝟐
= 3 (10cm)(12cm) + 2
𝟏𝟐𝐜𝐦 𝐱 𝟑.𝟔𝒄𝒎
𝟐
= 3 (120cm²) + 2
𝟒𝟑.𝟐𝐜𝐦²
𝟐
= 360cm² + 43.2cm²
SA = 403.2cm²

59. 5. Zach had 700 marbles. He shared 145 marbles and put the
remaining marbles equally in 5 jars. How many marbles were in each
jar?
LET’S TRY!
B. Illustrate a flat model of each rectangular prism. Find the
surface area.
Use the following dimensions:Length (l) Width (w) Height (h)
1. 5 cm 9 cm 11 cm _____________________
2. 6 in 3.5 in 7 in _____________________
3. 18 mm 20 mm 15 mm _____________________
4. 1 dm 3 dm 2.5 dm _____________________
5. 6 cm 12 cm 15 cm ____________________

60. SA = 2lw + 2lh + 2wh
= 2 (5cm)(9cm) + 2 (5cm)(11cm) + 2 (9cm)(11cm)
= 90cm² + 110cm² + 198cm²
SA = 398 cm²

61. SA = 2lw + 2lh + 2wh
= 2 (6in)(3.5in) + 2 (6in)(7in) + 2 (3.5in)(7in)
= 42in² + 84in² + 49in²
SA = 175 in²

62. SA = 2lw + 2lh + 2wh
= 2 (18mm)(20mm) + 2 (18mm)(15mm) + 2 (20mm)(15mm)
= 720mm² + 540mm² + 600mm²
SA = 1,860 mm²

63. SA = 2lw + 2lh + 2wh
= 2 (1dm)(3dm) + 2 (1dm)(2.5dm) + 2 (2dm)(2.5dm)
= 6dm² + 5dm² + 15dm²
SA = 26 dm²

64. SA = 2lw + 2lh + 2wh
= 2 (6cm)(12cm) + 2 (6cm)(15cm) + 2 (12cm)(15cm)
= 144cm² + 180cm² + 360cm²
SA = 684 cm²