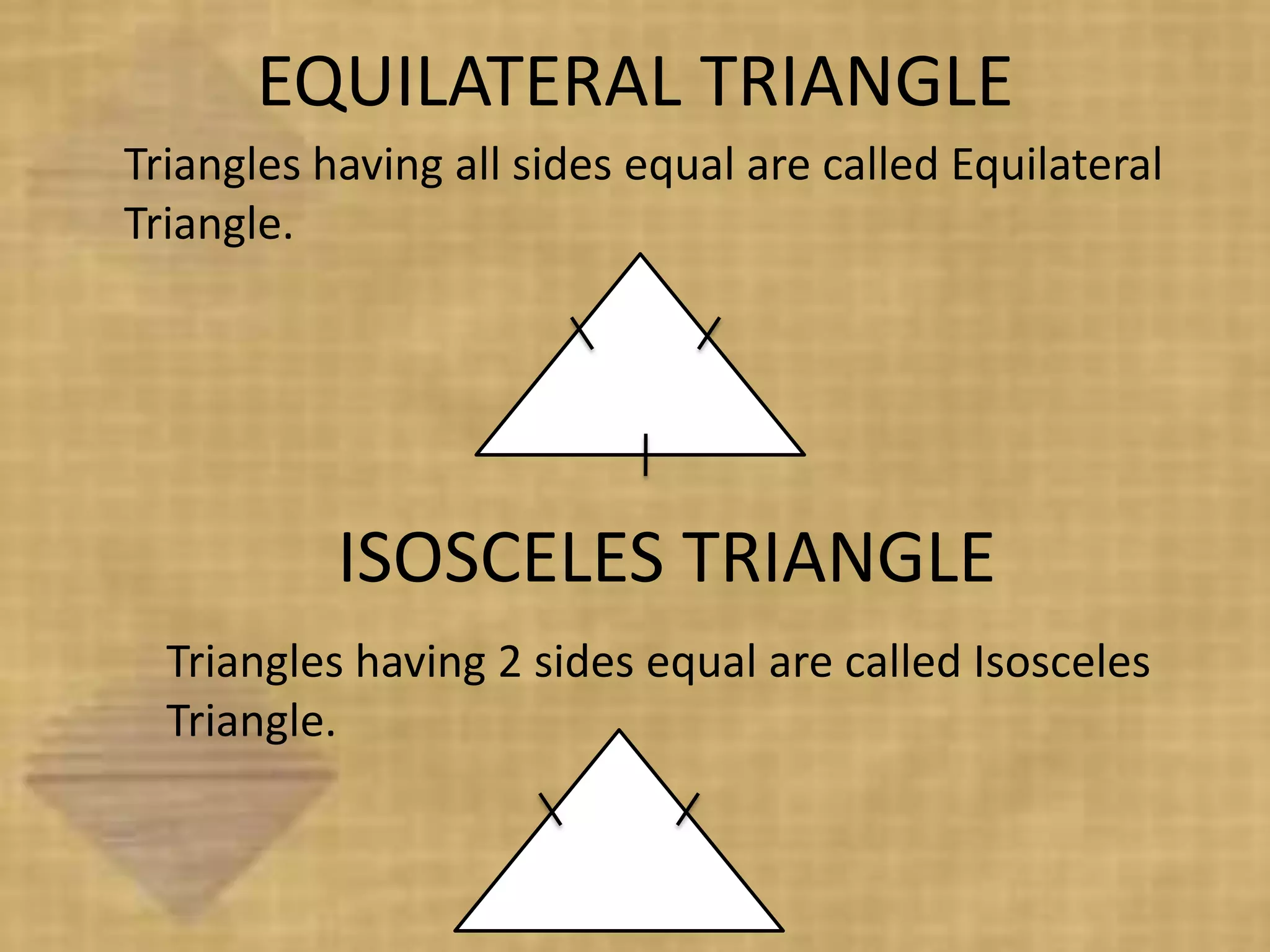
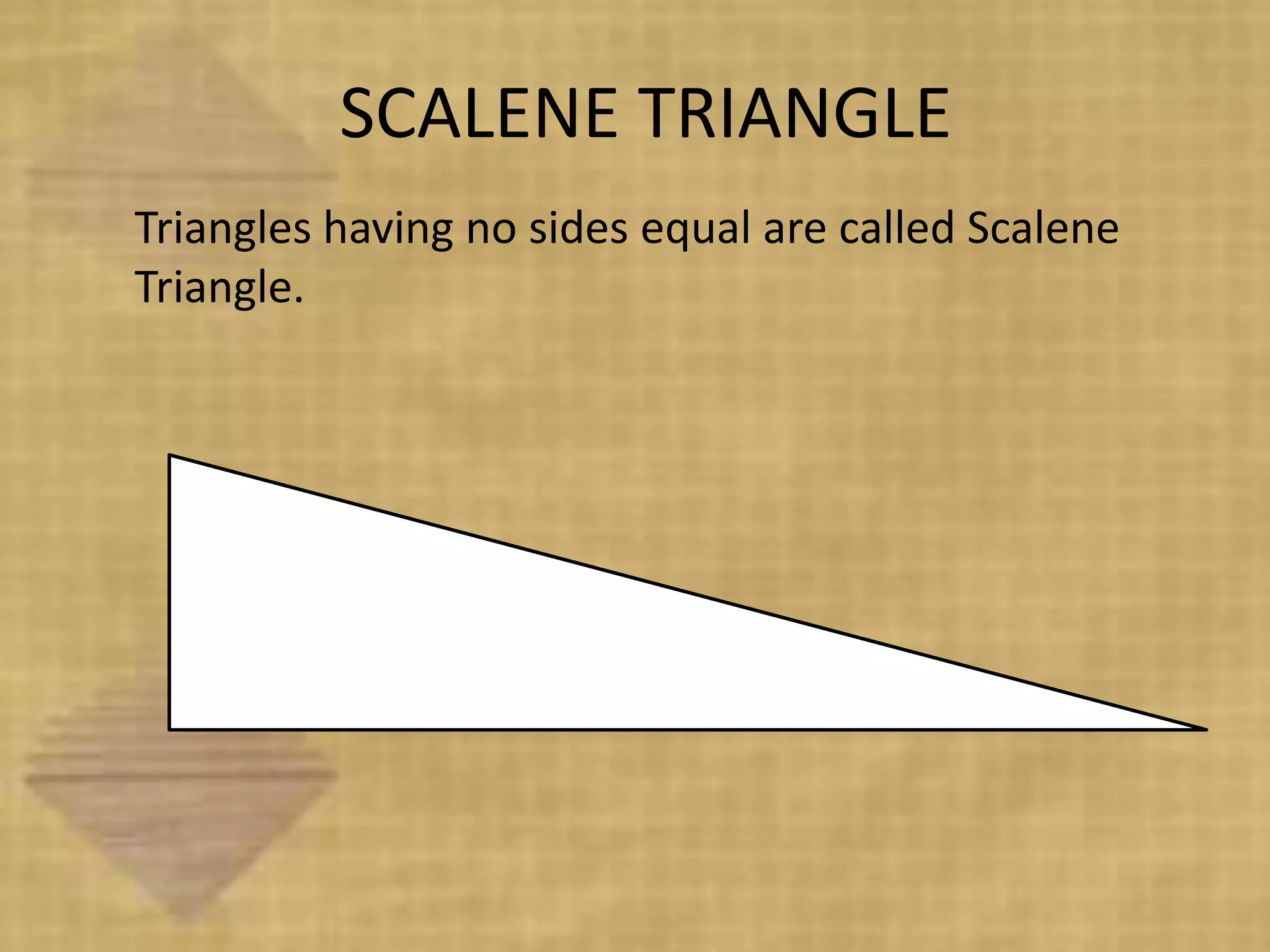
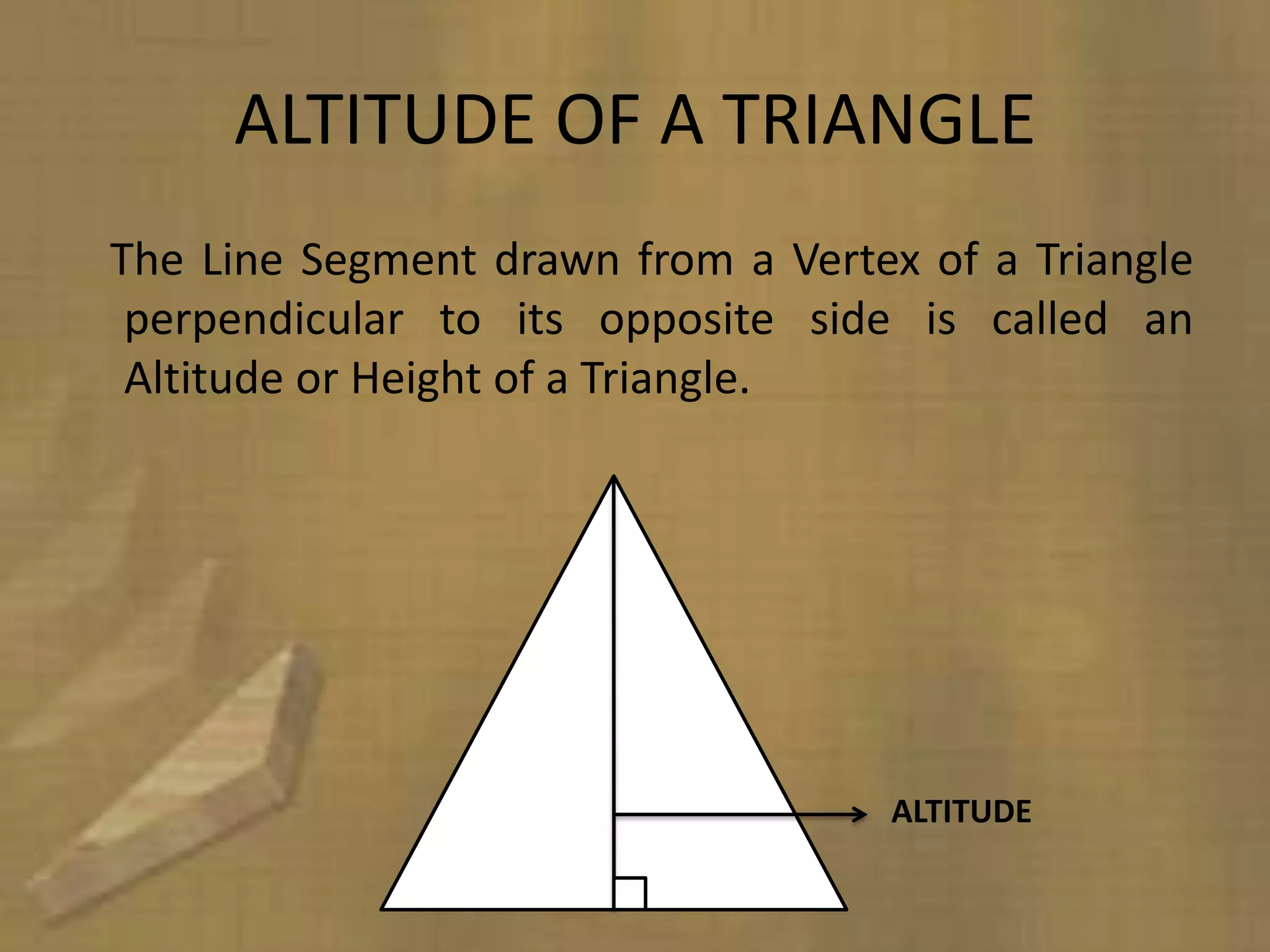
Triangles are three-sided polygons that have three angles and three sides. There are three main types of triangles based on side lengths: equilateral (all sides equal), isosceles (two sides equal), and scalene (no sides equal). The interior angles of any triangle always sum to 180 degrees. Important triangle properties include the exterior angle theorem, Pythagorean theorem, and congruency criteria like SSS, SAS, ASA. Common secondary parts are the median, altitude, angle bisector, and perpendicular bisector. The area of triangles can be found using Heron's formula or other formulas based on side lengths and types of triangles.

1. TRIANGLES

2. CONTENTS
• TRIANGLES
1. DEFINITION
2. TYPES
3. PROPERTIES
4. SECONDARY PART
5. CONGRUENCY
6. AREA

3. TRIANGLES
A triangle is a 3-sided polygon. Every triangle has three
sides, three vertices and three angles. On the basis of sides
of a triangle, triangles are of three types, An Equilateral
Triangle, An Isosceles Triangle and A Scalene Triangle. All
triangles are convex and bicentric. That portion of the plane
enclosed by the triangle is called the triangle interior, while
the remainder is the exterior.
The study of triangles is sometimes known as triangle
geometry and is a rich area of geometry filled with
beautiful results and unexpected connections.

4. TYPES
OF
TRIANGLES

5. TYPES OF TRIANGLES
On Basis of Length of Sides, there are 3 types of Triangles
• Equilateral Triangle
• Isosceles Triangle
• Scalene Triangle
On Basis of Angles, there are 3 types of triangles
• Acute Angled Triangle
• Obtuse Angled Triangle
• Right Angled Triangle

6. EQUILATERAL TRIANGLE
Triangles having all sides equal are called Equilateral
Triangle.
ISOSCELES TRIANGLE
Triangles having 2 sides equal are called Isosceles
Triangle.

7. SCALENE TRIANGLE
Triangles having no sides equal are called Scalene
Triangle.

8. ACUTE ANGLED TRIANGLE
Triangles whose all angles are acute angle are
called Acute Angled Triangle.
OBTUSE ANGLED TRIANGLE
Triangles whose 1 angle is obtuse angle are
called Obtuse Angled Triangle.
RIGHT ANGLED TRIANGLE
Triangles whose 1 angle is right angle are
called Right Angled Triangle.

9. PROPERTIES
OF A
TRIANGLE

10. PROPERTIES OF A TRIANGLE
Triangles are assumed to be two-dimensional plane
figures, unless the context provides otherwise. In rigorous
treatments, a triangle is therefore called a 2-simplex.
Elementary facts about triangles were presented by Euclid
in books 1–4 of his Elements, around 300 BC.
The measures of the interior angles of the triangle always
add up to 180 degrees.

11. PROPERTIES OF A TRIANGLE
The measures of the interior angles of a triangle
in Euclidean space always add up to 180 degrees.
This allows determination of the measure of the
third angle of any triangle given the measure of
two angles. An exterior angle of a triangle is an
angle that is a linear pair to an interior angle. The
measure of an exterior angle of a triangle is equal
to the sum of the measures of the two interior
angles that are not adjacent to it; this is the
Exterior Angle Theorem. The sum of the
measures of the three exterior angles (one for
each vertex) of any triangle is 360 degrees.

12. ANGLE SUM PROPERTY
Angle sum Property of a Triangle is that the sum of
all interior angles of a Triangle is equal to 180˚.
EXTERIOR ANGLE PROPERTY
Exterior angle Property of a Triangle is that An
exterior angle of the Triangle is equal to sum of two
opposite interior angles of the Triangle.

13. PYTHAGORAS THEOREM
Pythagoras Theorem is a theorem given by
Pythagoras. The theorem is that In a Right Angled
Triangle the square of the hypotenuse is equal to the
sum of squares of the rest of the two sides.
HYPOTENUSE

14. SECONDARY
PARTS OF A
TRIANGLE

15. MEDIAN OF A TRIANGLE
The Line Segment joining the midpoint of the base of
the Triangle is called Median of the Triangle.
OR
A Line Segment which connects a vertex of a Triangle
to the midpoint of the opposite side is called Median
of the Triangle.
MEDIAN

16. ALTITUDE OF A TRIANGLE
The Line Segment drawn from a Vertex of a Triangle
perpendicular to its opposite side is called an
Altitude or Height of a Triangle.
ALTITUDE

17. PERPENDICULAR BISECTOR
A line that passes through midpoint of the
triangle or the line which bisects the third
side of the triangle and is perpendicular to it is
called the Perpendicular Bisector of that
Triangle.
PERPENDICULAR
BISECTOR

18. ANGLE BISECTOR
A line segment that bisects an angle of a
triangle is called Angle Bisector of the triangle.
ANGLE BISECTOR

19. CONGRUENCY
OF
A
TRIANGLE

20. SSS CRITERIA OF CONGRUENCY
If the three sides of one Triangle are equal to
the three sides of another Triangle. Then the
triangles are congruent by the SSS criteria.
SSS criteria is called Side-Side-Side criteria of
congruency.

21. SAS CRITERIA OF CONGRUENCY
If two sides and the angle included between
them is equal to the corresponding two sides
and the angle between them of another
triangle. Then the both triangles are
congruent by SAS criteria i.e. Side-Angle-Side
Criteria of Congruency.

22. ASA CRITERIA OF CONGRUENCY
If two angles and a side of a Triangle is equal
to the corresponding two angles and a side of
the another triangle then the triangles are
congruent by the ASA Criteria i.e. Angle-Side-
Angle Criteria of Congruency.

23. RHS CRITERIA OF CONGRUENCY
If the hypotenuse, and a leg of one right
angled triangle is equal to corresponding
hypotenuse and the leg of another right
angled triangle then the both triangles are
congruent by the RHS criteria i.e. Right Angle-
Hypotenuse-Side Criteria of Congruency.

24. AREA
OF A
TRIANGLE

25. HERON’S FORMULA
Heron’s Formula can be used in finding area of
all types of Triangles. The Formula is ::->
AREA =
S = Semi-Perimeter
a,b,c are sides of the Triangle

26. FORMULA FOR ISOSCELES TRIANGLE
Area of an Isosceles Triangle
=
b = base
a = length of equal sides

27. FORMULA FOR RIGHT ANGLED
TRIANGLE
½ x base x height

28. PYTHAGORAS EUCLID PASCAL
MATHEMATICIANS RELATED TO TRIANGLES

29. THANKS