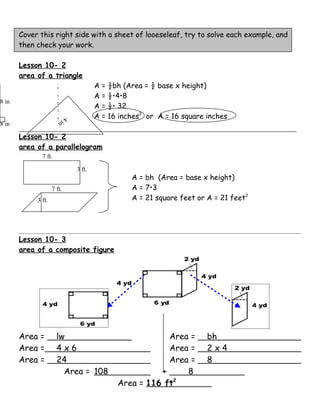
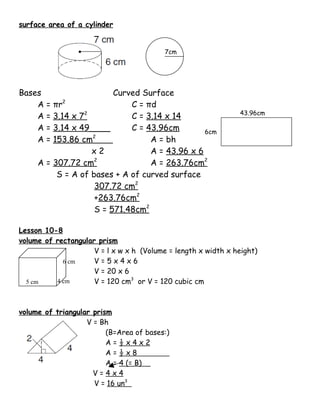
The document is a study guide for geometry concepts including formulas for area, perimeter, surface area, and volume of various shapes. It includes yes or no questions to check understanding of formulas and definitions for triangles, parallelograms, circles, prisms, pyramids, cylinders, and cones. It then provides examples of applying the formulas to calculate measurements of different shapes.

1. PARENT STUDY GUIDE
YES NO I know the formula for the area of triangle
YES NO I know the formula for the area of a parallelogram
YES NO I know the formula for the surface area of a parallelogram
YES NO I know the formula for volume
YES NO I know the formula for the area of a circle
YES NO I know the formula for the circumference of a circle
YES NO I know the numerical value for pi
YES NO I know how to find the area of triangle
YES NO I know how to find the area of a parallelogram
YES NO I know how to find the surface area of a parallelogram
YES NO I know how to find volume
YES NO I know how to find the area of a circle
YES NO I know how to find the circumference of a circle
YES NO I know the definition of face for a three-dimensional figure
YES NO I know the definition of vertex for a three-dimensional figure
YES NO I know the definition of edge for a three-dimensional figure
YES NO I can identify a cylinder
YES NO I can identify a cube (square prism) #1
YES NO I can identify a rectangular prism #2
YES NO I can identify a triangular prism #3
YES NO I can identify a cylinder #4
YES NO I can identify a rectangular pyramid #5
YES NO I can identify a triangular pyramid #6
YES NO I can identify a cone #7
7
3 4
1 2 5 6

2. Cover this right side with a sheet of looeseleaf, try to solve each example, and
then check your work.
Lesson 10- 2
area of a triangle
A = ½bh (Area = ½ base x height)
A = ½•4•8
8 in
A = ½• 32
in
4 A = 16 inches2 or A = 16 square inches
8 in
Lesson 10- 2
area of a parallelogram
7 ft.
3 ft.
A = bh (Area = base x height)
7 ft. A = 7•3
3 ft. A = 21 square feet or A = 21 feet2
Lesson 10- 3
area of a composite figure
Area = lw Area = bh
Area = 4x6 Area = 2x4
Area = 24 Area = 8
Area = 108 + 8
Area = 116 ft2

3. Lesson 10- 4
Comparing Area & Perimeter
When the original figure’s length and width multiplies by __2________, the
perimeter multiplies by ____2____ and the area multiplies by ___22(4)_____.
Lesson 10-5
Circles E
Name the circle A D
Name the two radii of the circle. AB, AC, AD
A
Name the chord of the circle. EC C B
What does the diameter measure? 4cm 4cm
What does the radius measure? 2cm
circumference of a circle
(know how to solve when the diameter & radius are given)
C= πd (Circumference = pi x diameter)
(Cherry Pie is delicious)
18 cm C = 3.14 x 18
C = 56.62 cm
area of a circle
(know how to solve when the diameter & radius are given)
A = πr2 (Area = pi x radius squared)
(Apple pies are too2)
4 ft. A = 3.14 x 42
A = 3.14 x 16 (be sure you do 4 x 4 NOT 4 x 2)
A = 50.24 ft2 or A = 50.24 square feet

4. Lesson 10-6
Solid Figures
cube (square prism) #1
rectangular prism #2
triangular prism #3
cylinder #4
rectangular pyramid #5
triangular pyramid #6
cone #7
7
3 4
1 2 5 6
Lesson 10-7
surface area of a rectangular prism
top (& bottom) add the area for all six sides
si 6 m
de
A front = 9 x 6 = 54 m2
front (& back) A back = 9 x 6 = 54 m2
5m
9m
A top = 9 x 5 = 45 m2
A bottom = 9 x 5 = 45 m2
A left side= 6 x 5 = 30 m2 You can also
A right side= 6 x 5 = 30 m2 multiply the area
S = 258 m2 of one side by the
number of sides
surface area of a triangular prism there are – refer
add the area for all six sides to your notes.
A front = ½ 3 x 4 = 6 m2
A back = ½ 3 x 4 = 6 m2
A side = 6 x 3 = 18 m2
A side = 6 x 3 = 18 m2
A side = 6 x 3 = 18 m2
4m
6m S = 66 m2
3m

5. surface area of a cylinder
7cm
Bases Curved Surface
A= πr2 C = πd
43.96cm
A= 3.14 x 72 C = 3.14 x 14
A= 3.14 x 49____ C = 43.96cm 6cm
2
A= 153.86 cm A = bh
x2 A = 43.96 x 6
A = 307.72 cm2 A = 263.76cm2
S = A of bases + A of curved surface
307.72 cm2
+263.76cm2
S = 571.48cm2
Lesson 10-8
volume of rectangular prism
V = l x w x h (Volume = length x width x height)
6 cm V=5x4x6
V = 20 x 6
5 cm 4 cm V = 120 cm3 or V = 120 cubic cm
volume of triangular prism
V = Bh
(B=Area of bases:)
A=½x4x2
A=½x8
A = 4 (= B)
V=4x4
V = 16 un3

6. volume of a cylinder
V = πr2h
V = 3.14 x 32 x 5
V = 3.14 x 9 x 5
V = 3.14 x 45
V = 141.3
V = 141.3un3