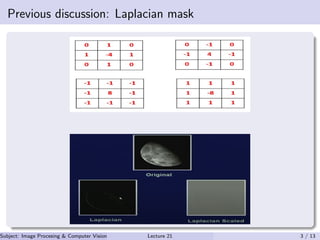
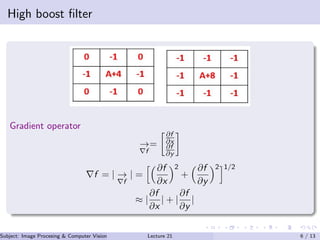
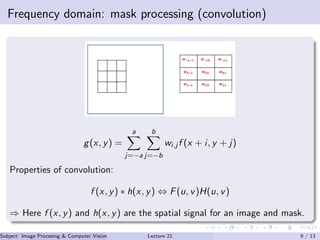
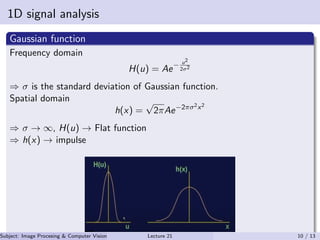
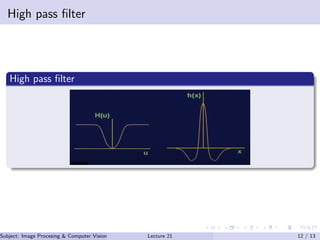
This document discusses frequency domain techniques for image enhancement. It outlines mask processing and frequency domain techniques. It discusses unsharp masking and high boost filtering for sharpening images. It also discusses taking the first order derivative of an image. In the frequency domain, mask processing is equivalent to convolution. A Gaussian function is used as a low pass filter mask in the frequency domain. Examples of low pass and high pass filters are also provided. References for further reading on image processing and computer vision are listed at the end.

1. Frequency Domain Operation for Image Enhancement
Subject: Image Procesing & Computer Vision
Dr. Varun Kumar
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 1 / 13

2. Outlines
1 Mask processing technique
Unsharp masking
High boost filter
First order derivative operator
2 Frequency domain technique
3 References
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 2 / 13

3. Previous discussion: Laplacian mask
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 3 / 13

4. Composite mask
Original image→ Diagonal neighbors are zero → Diagonal neighbors are non-zero
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 4 / 13

5. Sharpening an image
fs(x, y)
Sharpened image
= f (x, y) − ¯f (x, y)
Blurred f (x,y)
Unsharp masking:
⇒ High boost filtering:
fhb(x, y) = Af (x, y) − ¯f (x, y) A ≥ 1
= (A − 1)f (x, y) + f (x, y) − ¯f (x, y)
fs (x,y)
Using Laplacian
fhb(x, y) = Af (x, y) − ∆2
f (x, y)
= Af (x, y) + ∆2
f (x, y)
Using laplacian first expression is used when mask center is -ve and second
for mask center is -ve.
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 5 / 13

6. High boost filter
Gradient operator
→
f
=
∂f
∂x
∂f
∂y
f = | →
f
| =
∂f
∂x
2
+
∂f
∂y
2 1/2
≈ |
∂f
∂x
| + |
∂f
∂y
|
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 6 / 13

7. Continued–
For discrete data
∂f
∂x
≈ f (x + 1, y − 1) + f (x + 1, y + 1) + 2f (x + 1, y) −
f (x − 1, y − 1) + f (x − 1, y + 1) + 2f (x − 1, y)
First order derivative
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 7 / 13

8. Example: First order derivative on image
⇒ Left side image is an original image.
⇒ Right side image is observed after the taking the first order derivative.
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 8 / 13

9. Frequency domain: mask processing (convolution)
g(x, y) =
a
j=−a
b
j=−b
wi,j f (x + i, y + j)
Properties of convolution:
f (x, y) ∗ h(x, y) ⇔ F(u, v)H(u, v)
⇒ Here f (x, y) and h(x, y) are the spatial signal for an image and mask.
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 9 / 13

10. 1D signal analysis
Gaussian function
Frequency domain
H(u) = Ae− u2
2σ2
⇒ σ is the standard deviation of Gaussian function.
Spatial domain
h(x) =
√
2πAe−2πσ2x2
⇒ σ → ∞, H(u) → Flat function
⇒ h(x) → impulse
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 10 / 13

11. Low filter mask
High pass filter using Gaussian expression
H(u) = A(1 − e− u2
2σ2 )
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 11 / 13

12. High pass filter
High pass filter
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 12 / 13

13. References
M. Sonka, V. Hlavac, and R. Boyle, Image processing, analysis, and machine vision.
Cengage Learning, 2014.
D. A. Forsyth and J. Ponce, “A modern approach,” Computer vision: a modern
approach, vol. 17, pp. 21–48, 2003.
L. Shapiro and G. Stockman, “Computer vision prentice hall,” Inc., New Jersey,
2001.
R. C. Gonzalez, R. E. Woods, and S. L. Eddins, Digital image processing using
MATLAB. Pearson Education India, 2004.
Subject: Image Procesing & Computer Vision Dr. Varun Kumar (IIIT Surat)Lecture 21 13 / 13