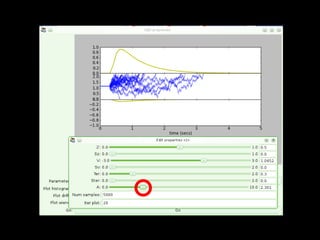
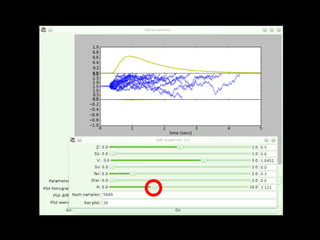
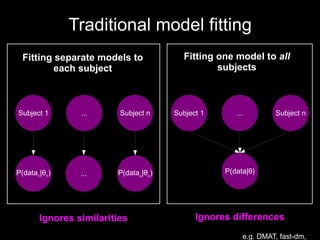
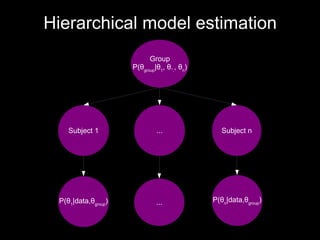
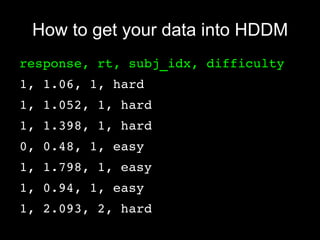
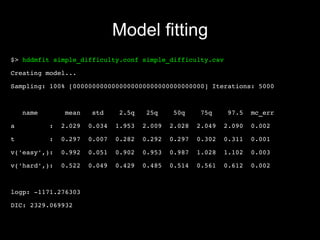
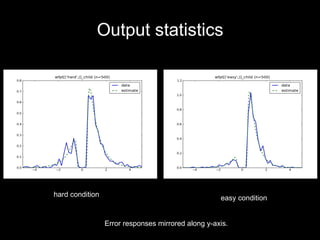
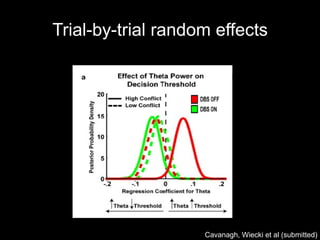
HDDM is a hierarchical Bayesian model that fits drift-diffusion models to behavioral data from multiple subjects. It estimates both group-level and subject-specific parameters, leveraging information across subjects to obtain more reliable estimates. This allows modeling experimental effects like difficulty while accounting for individual differences. HDDM implements efficient Markov chain Monte Carlo sampling in Python to estimate the full posterior distribution. It provides tools to assess model fit and visualize parameter estimates.

1. HDDM: Hierarchical Bayesian Drift-Diffusion Modeling Thomas V. Wiecki & Imri Sofer, Michael J. Frank

2. Drift-Diffusion Model

5. Traditional model fitting Fitting separate models to each subject Fitting one model to all subjects e.g. DMAT, fast-dm, EZ Ignores similarities Ignores differences Subject 1 ... Subject n P( data 1 | θ 1 ) ... P( data n | θ n ) P( data| θ ) Subject 1 ... Subject n Subject 1 ... Subject n Subject 1 ... Subject n

6. Hierarchical model estimation Subject 1 ... Subject n Group P( θ group |θ 1 , θ. , , θ n ) P(θ 1 |data, θ group ) ... P(θ n |data, θ group )

7. Hierarchical Bayesian estimation Pro Adequately maps experimental structure onto model

8. Needs less data for individual subject estimation

9. Constraining of subject parameters (helps with extreme fits)

10. Estimation of full posterior, not just maximum

11. ... Contra Computationally expensive (sampling, e.g. MCMC)

12. Correct model behavior can be hard to assess (e.g. chain convergence)

13. Methods still in development

14. Hierarchical Bayesian estimation (via PyMC) of parameters of the DDM in Python. Ratcliff, Vandekerckhove, Tuerlinckx, Lee, Wagenmakers Heavily optimized likelihood functions Navarro & Fuss (2009) likelihood

15. Collapsed model for inter-trial variabilities Flexible creation of complex models tailored to specific hypotheses (e.g. separate drift-rate parameters for different stimulus types).

16. Several convergence and goodness-of-fit diagnostics

17. Validated : integrated tests check if parameters from simulated data can be recovered HDDM

18. ...it works!