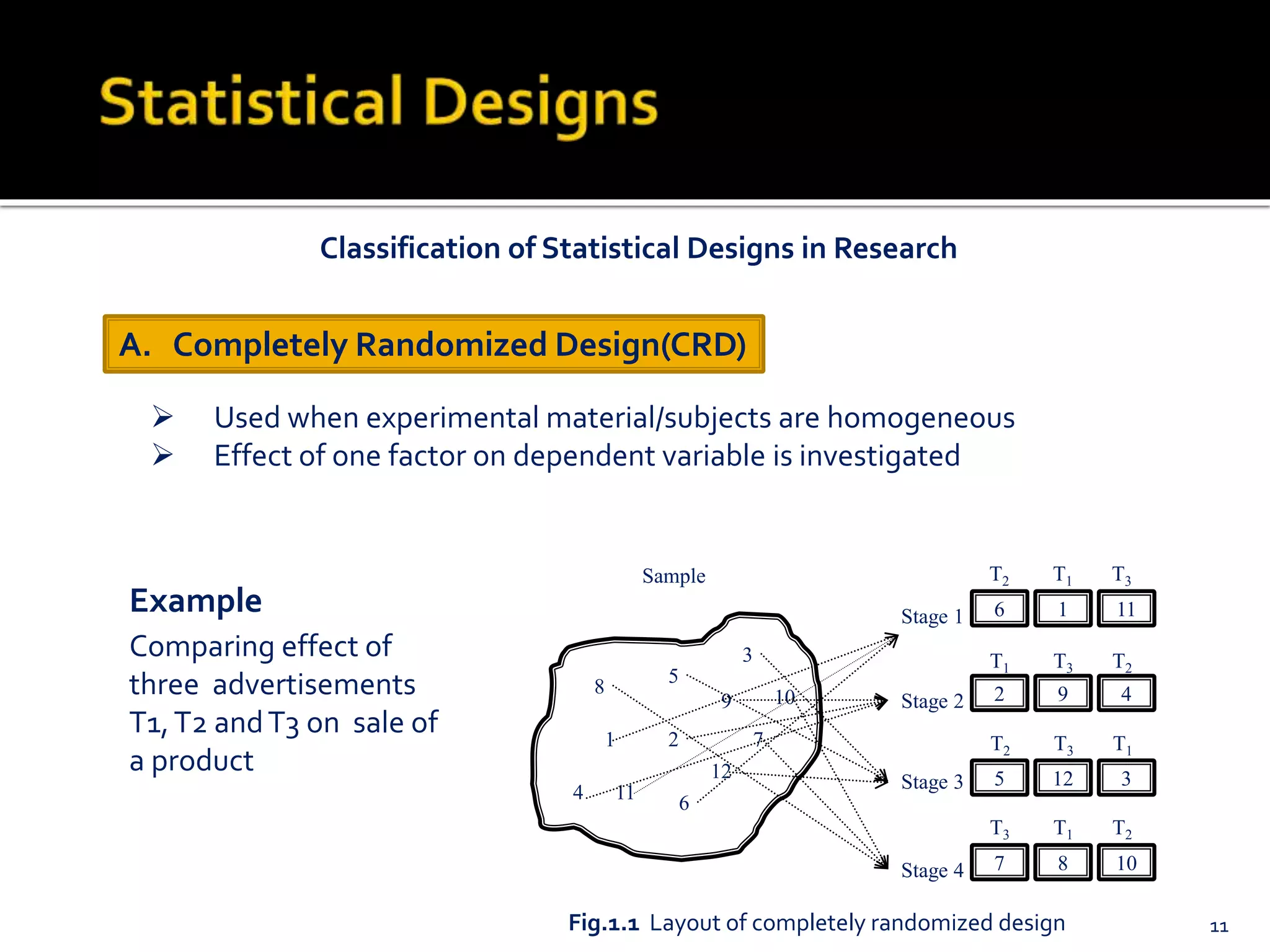
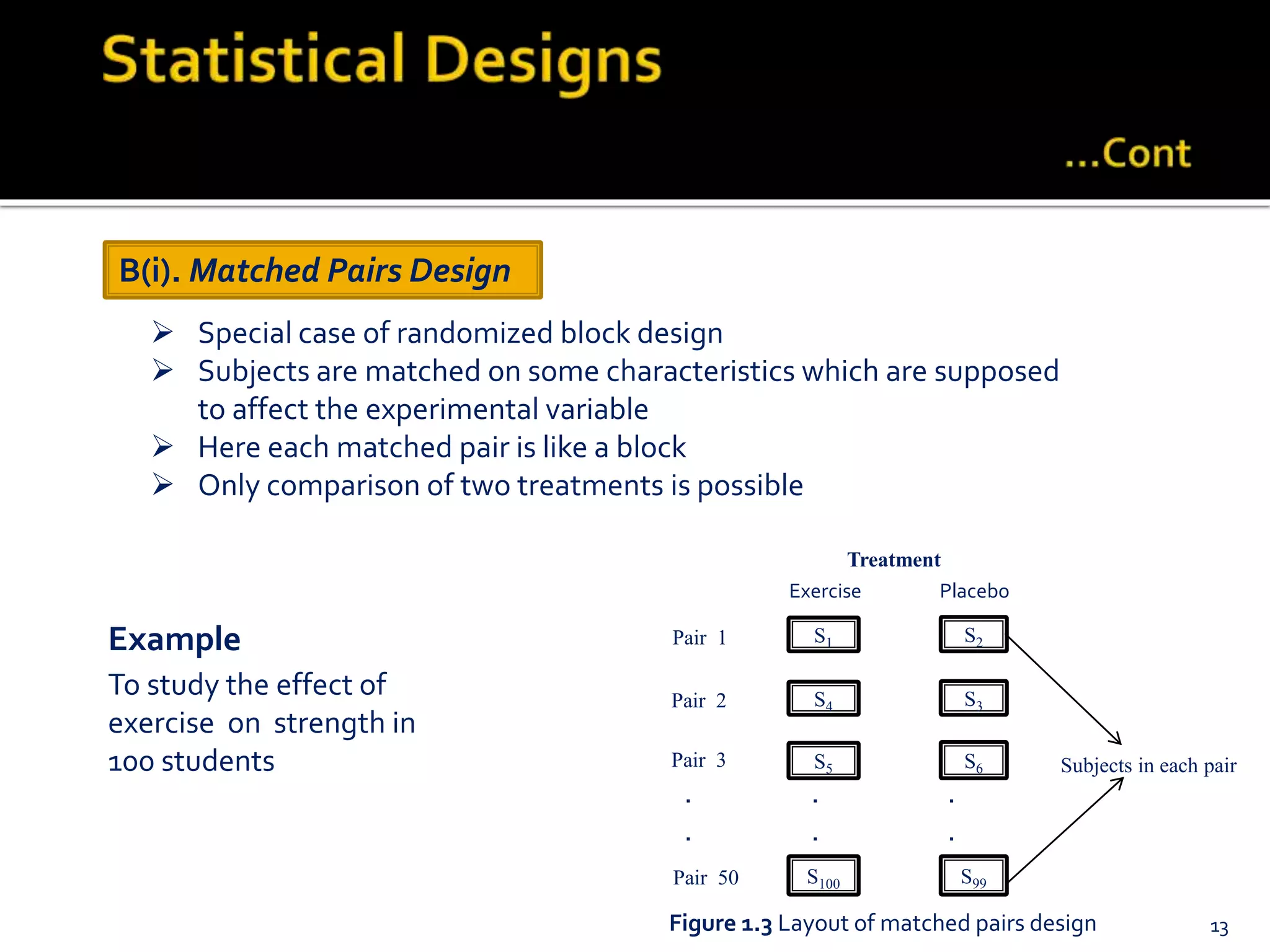
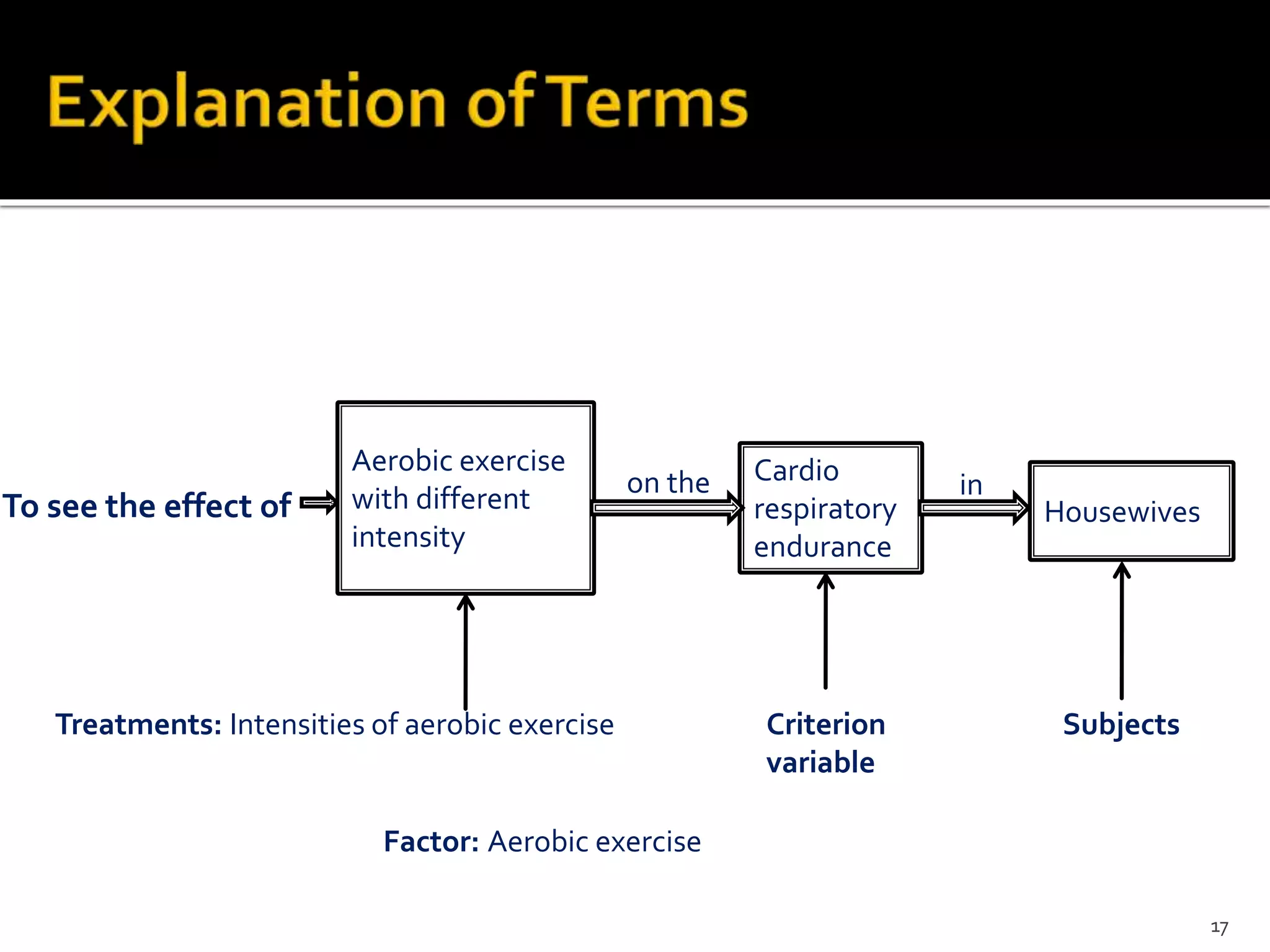
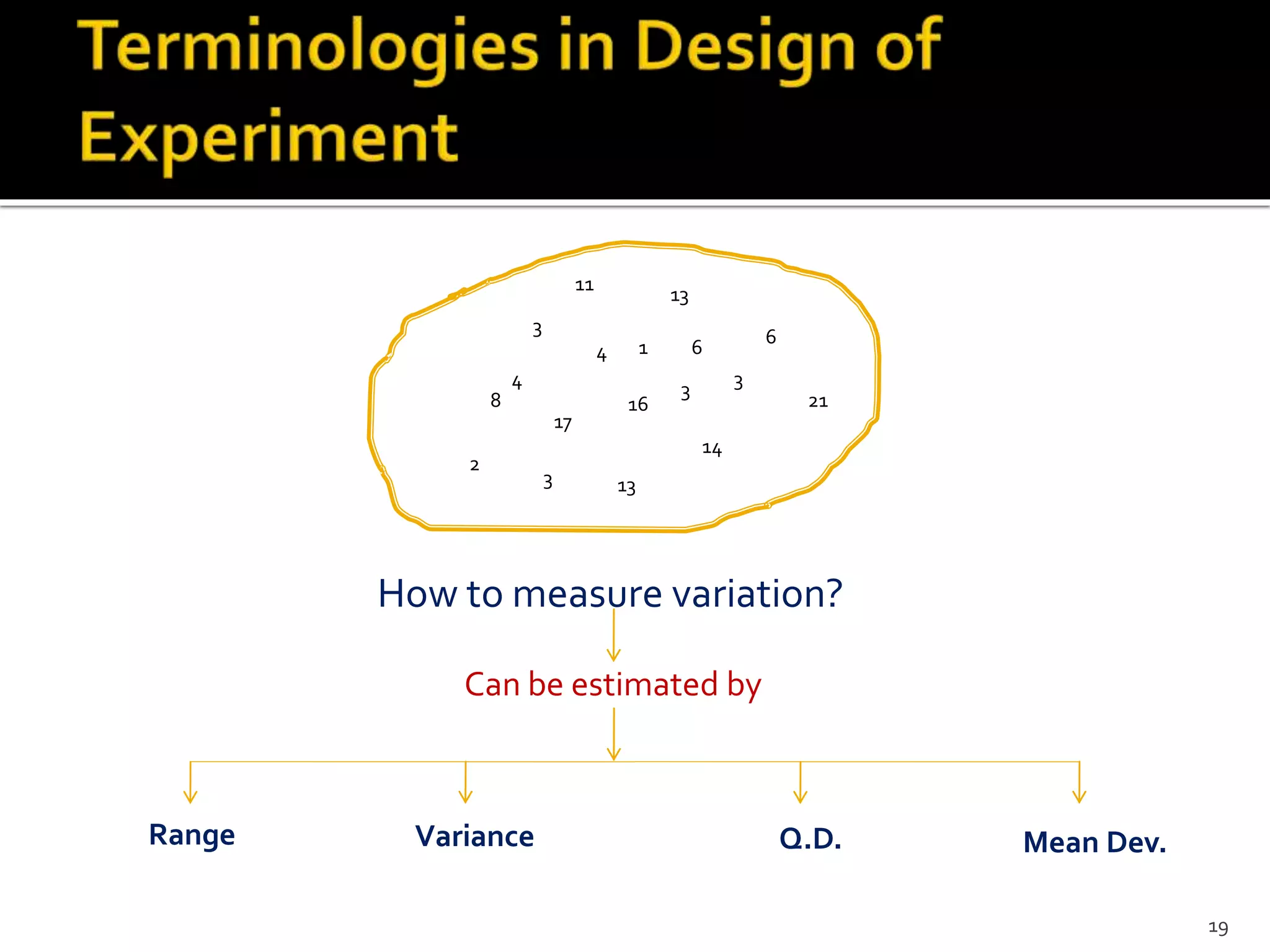
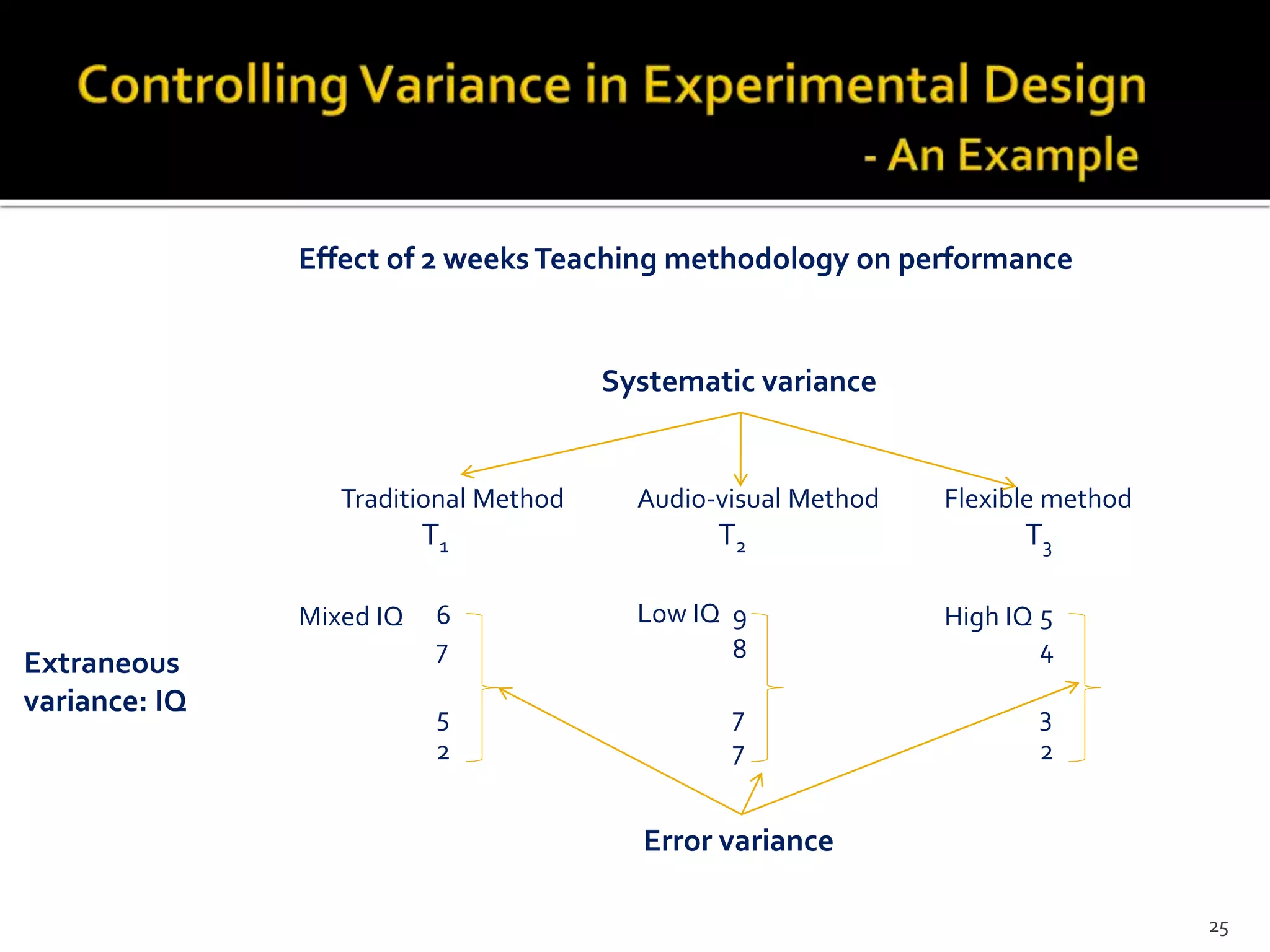
The document outlines various experimental designs in statistical research, emphasizing the importance of hypothesis testing and the relationship between independent and dependent variables. It discusses different design types, including completely randomized, randomized block, matched pairs, and Latin square designs, along with their applications and limitations. Key concepts like randomization, replication, and measurement of variation are highlighted to enhance the validity and reliability of experimental outcomes.

1. Presented by
Dr.J.P.Verma
MSc (Statistics), PhD, MA(Psychology), Masters(Computer Application)
Professor(Statistics)
Lakshmibai National Institute of Physical Education, Gwalior, India
(Deemed University)
Email: vermajprakash@gmail.com

2. To test a theory through deductive logic
To develop a theory through inductive logic
2

3. The exercise intensity with 65% maximum heart rate may
improve the cardio- respiratory endurance significantly.
By means of Hypothesis
Example
3

4. If most of the sports persons are medal winners from a
particular university their training programme
may be superior than the other universities.
By observing a phenomenon
Example
4

5. 5
This Presentation is based on
Chapter 1 of the book
Repeated Measures Design
for Empirical Researchers
Published by Wiley, USA
Complete Presentation can be accessed on
Companion Website
of the Book

6. To investigate some kinds of relationship between
independent and dependent variables.
6

7.  lack cause and effect relationships
 Reduced internal validity
Non Experimental or Correlational
Experimental
 Explain cause and effect relationships
 Higher internal validity
7

8. Experimenter manipulates independent variable
to see its impact on dependent variable
by controlling extraneous factors
8

9. Organizing a controlled experiment to generate data
for understanding the causes of variation
9

10. - Ensures homogeneity in the experimental groups
- Enhances external and internal validity in the study
Randomization
Replication
- Repeating an experiment a number of times on subjects/
experimental units
- A way of reducing experimental error by including an extraneous variable
in the experiment.
- Heterogeneous experimental units are divided into homogenous blocks
- Treatments are randomly allocated in these blocks.
Blocking
10

11.  Used when experimental material/subjects are homogeneous
 Effect of one factor on dependent variable is investigated
Classification of Statistical Designs in Research
A. Completely Randomized Design(CRD)
5
8
12
7
3
9 10
1 2
11
6
4
6 1 11Stage 1
2 9 4Stage 2
5 12 3Stage 3
7 8 10Stage 4
T2 T1 T3
T1 T3 T2
T2 T3 T1
T3 T1 T2
Sample
Comparing effect of
three advertisements
T1,T2 andT3 on sale of
a product
Example
Figure 1.1 Layout of the completely randomized design
Fig.1.1 Layout of completely randomized design 11

12.  Used when experimental material/subjects are heterogeneous
 Effect of one factor on dependent variable is investigated by
introducing the blocking variable in experiment.
B. Randomized Block Design
T1 T3 T2Low IQ
Average IQ
High IQ
Block:IQ
T3 T1 T2
T2 T3 T1
Allocation of
treatments in block
Block 1
Block 2
Block 3
Subjects in block
Fig.1.2 Layout of randomized block design
To study the effect of three
different types of teaching
methodologies T1,T2 and
T3 on learning efficiency.
Example
12

13.  Special case of randomized block design
 Subjects are matched on some characteristics which are supposed
to affect the experimental variable
 Here each matched pair is like a block
 Only comparison of two treatments is possible
B(i). Matched Pairs Design
S1
S4
S5
S100
Subjects in each pair
Pair 1
Pair 2
Pair 3
Treatment
S2
S3
S6
S99
Exercise Placebo
. . .
. . .
Pair 50
Figure 1.3 Layout of matched pairs design
To study the effect of
exercise on strength in
100 students
Example
13

14. C. Latin Square Design
 In this design random variation of two factors is controlled
 Two blocking factor can be taken in this design
 Number of rows columns and treatments are required to be same in this design.
 Each treatment can occur only once in the corresponding row and column.
Low
Average
High
Block:IQ
Fig.1.2 Layout of Latin square design
To study the effect of three
different types of teaching
methodologies T1,T2 and
T3 on learning efficiency.
Example
14
T1 T2 T3
T3 T1 T2
T2 T3 T1
Block: Age
Teens
Mid
age
Old
age

15. If factors A(exercise intensity)
has three levels(low , medium
and high) and B(Environment)
also has three levels(hot,
humid and cold) then nine
treatment groups are
required.
To investigate the effect of two or more factors
on a dependent variable simultaneously
Example
Low
Medium
High
Hot Humid Cold
Cells
Subjects in
each cell
FactorA:MentalExercise
Factor B: Environment
Figure 1.4 Layout of 3×3 factorial experiment
in CRD
15
DependentVariable: Task efficiency

16. - Experimental unit on which experiment is conducted
Subject
Treatment
- Levels of the independent variable whose effect is to be seen on the
dependent variable.
- A variable of interest
- An independent variable whose effect is to be seen on the
dependent variable
CriterionVariable
Factor
16

17. To see the effect of
Aerobic exercise
with different
intensity
on the Cardio
respiratory
endurance
in
Housewives
SubjectsTreatments: Intensities of aerobic exercise
Factor: Aerobic exercise
Criterion
variable
17

18. - Spread of Scores
Variation
- Measure ofVariation
Variance
18

19. 11
4
3
1
16
3
14
13
6
6
3
21
4
8
17
3
2
13
How to measure variation?
Can be estimated by
Range Variance Q.D. Mean Dev.
19

20.    22
x
N
1
  

 22
xx
1n
1
S
Population variance =
Mean Square Deviation
11
4
3
1
16
3
14
13
66
3
21
4
8
17
3
2
13
Population
Sample
11
2
14
3
Whether the population variance
can be estimated correctly by the
sample variance ?
S2 is an unbiased estimate of population variance
20

21.  Uncontrolled error in an experiment
 Attributed to non-assignable causes
 Individual variation
Experimental Error
21

22.  Extent of generalizibility of findings to the population
from which sample has been drawn.
External validity
 Extent to which one can say that the variation observed in
the Dependent variable(DV) is due to the variation in the
Independent variable(IV).
InternalValidity
22

23. Variation among scores
  

 22
xx
1n
1
SMean Square Deviation =
df
Variation

df
SS

23

24. Purpose of Experimental Design
Maximize SystematicVariance
Control ExtraneousVariance
Minimize ErrorVariance
24

25. Effect of 2 weeksTeaching methodology on performance
Traditional Method
T1
Flexible method
T3
Audio-visual Method
T2
6
7
5
2
9
8
7
7
5
4
3
2
Systematic variance
High IQLow IQ
Extraneous
variance: IQ
Error variance
Mixed IQ
25

26. 26
To buy the book
Repeated Measures Design
for Empirical Researchers
and all associated presentations
Click Here
Complete presentation is available on
companion website of the book