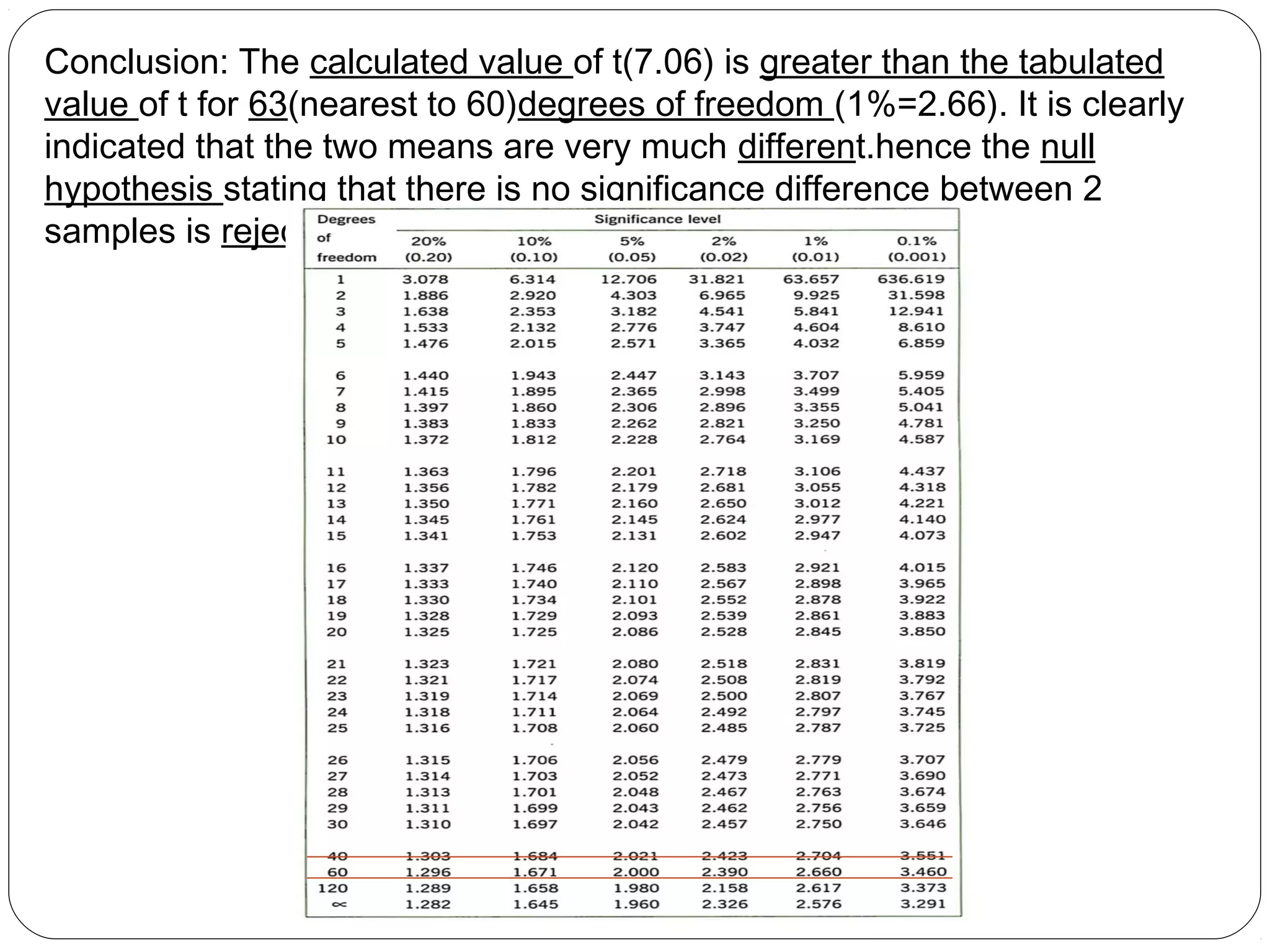
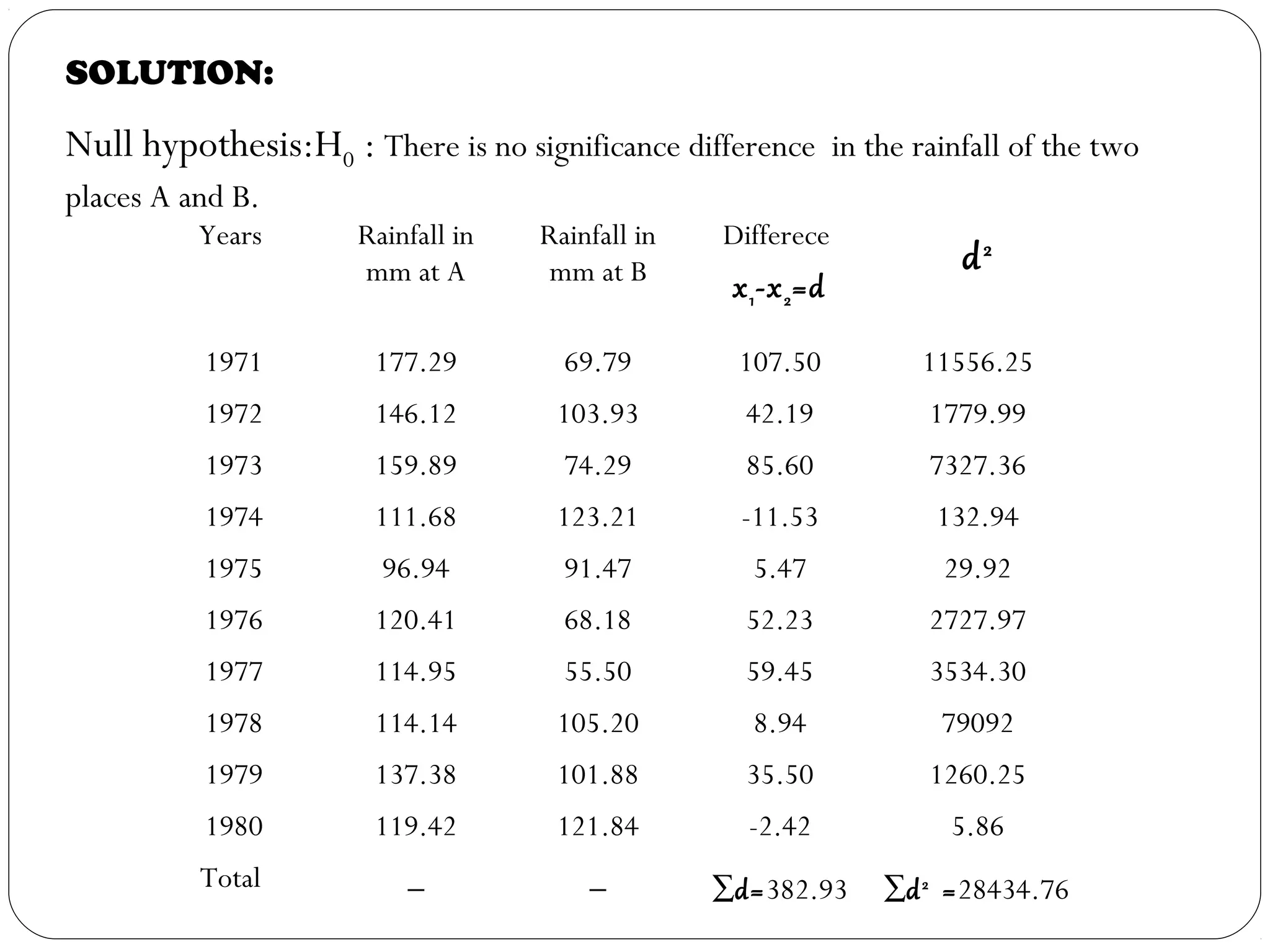
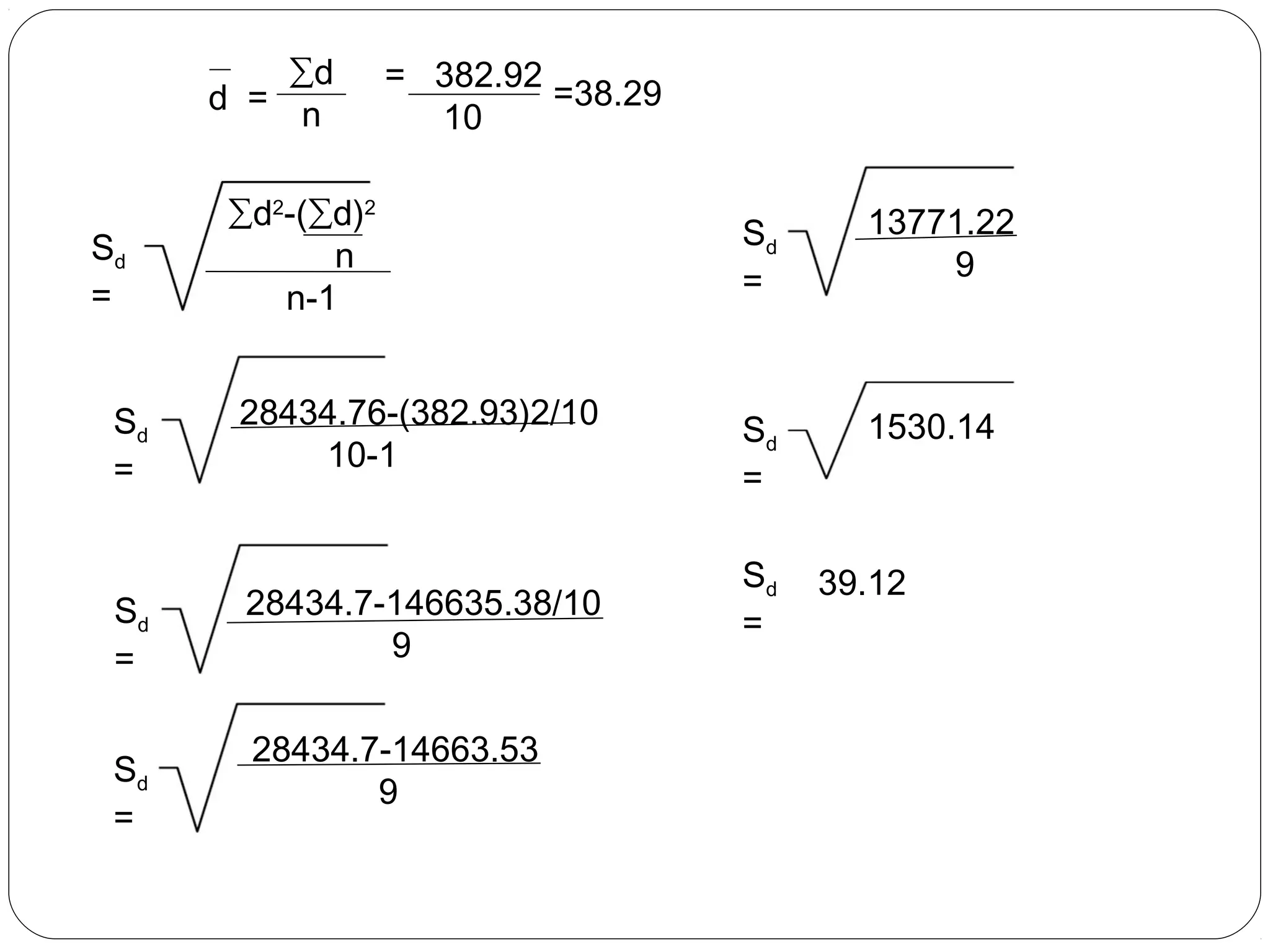
The document outlines a seminar on t-tests presented by Sayyed Heena Riyaz and Shaikh Qamrunnisa Abdul Wahid, focusing on biostatistics, definitions, history, types of t-tests, and practical examples. It explains the concept of the null hypothesis and details different t-test types, including large, small, and paired samples, with computed examples illustrating how to apply these tests in biological contexts. The document aims to provide a comprehensive understanding of statistical analysis techniques relevant to microbiology and quantitative biology.

1. t-test
Seminar presented by
SAYYED HEENA RIYAZ
&
SHAIKH QAMRUNNISA ABDUL
WAHID
MSC –I MICROBIOLOGY
(QUANTITATIVE BIOLOGY)

2. CONTENT:
1. Biostatistic
a. Defination
b. History
c. population
d. sample
e. null hypothesis
2. t-test
a. defination
b. history
3. Types of t-test
a. t-test for two small samples
b. t-test for two large samples
c. t-test for paired samples
4. Summary
5. previous years questions.

3. BIOSTATISTIC:
Biostatistics is the application of statistic to a wide range of topics in biology.
History:
 Ronald Fisher developed several basic statistical methods in support of his
work studying the field experiments.
 Sewall G. Wright developed F-statistics and methods of computing
them.
Ronald Fisher
Sewall G. Wright

4. POPULATION:
In statistic population is a well defined group which is being studied .
SAMPLE:
The selected part of the population is known as sample
NULL HYPOTHESIS:
There is no significance difference between population mean and sample
mean.

5. HISTORY:
 The t-statistic was introduced in 1908 by
William Sealy Gosset.
t-test:
 A t-test is a statistic that checks if two means are relaibly
different from each other.
 t-test findout significantly difference exists between two
groups of data.
William Sealy
Gosset

6. Types of t-test:
t-test for two large samples
t-test for two small
samples
t-test for paired samples

7. t-TEST FOR TWO LARGE SAMPLES:
 t=
Difference of means of two samples
standard error of difference
t =
x1-x2
Sd
=
Where,
• X1 = mean of first sample =
X2 = mean of second sample=
or
oror
or
• n1=number of observation in the first sample
n2= number of observation in the second sample
 Sample consisting of more than 30 observations or items is
called as large samples.

8. Where,
• Sd =Standard error of the difference ,Sd =
S1
2
= varience of first sample =
)
S2
2
= varience of second sample =
)
2
)
)
2
)
)
2
or
or
or
or
 Degrees of freedom= (n1+n2-2)

9. EXAMPLE-1:
Q-The following data relate to the days to flowering in two varieties of
mungbeans , G-65 &PS-16.Determine whether two means are significantly
different.
G-65 PS-16
n 30 35
mean 32 38
varience 9.62 14.23
SOLUTION:
Null hypothesis :There there is no significant difference between mean days to flowering in
both the varieties.
t =
x1-x2
Sd
Sd =
Where,

10. Sd =
0.84
t =
t =
Sd=
Sd=
Sd= 0.32
0.72
Sd=
t =
x1-x2
Sd
7.06
Degrees of freedom= (n1+n2-2) =(30+35-2) =(65-2) =63

11. Conclusion: The calculated value of t(7.06) is greater than the tabulated
value of t for 63(nearest to 60)degrees of freedom (1%=2.66). It is clearly
indicated that the two means are very much different.hence the null
hypothesis stating that there is no significance difference between 2
samples is rejected at P=1% .

12. EXAMPLE-2:
Q- Data recorded on the number of tomatoes per plant on two varieties of tomato. Compare
the mean of two varieties & give your conclusion.
Variety A:
6,8,10,12,12,14,11,6,8,9,12,14,13,7,8,10,12,14,15,7,8,13,16,9,10,13,14,13,14,14,9,11,
13,13,13,15,9,10,11,12,14,16,17,13,16,17,15,15,16,17.
Variety B:
8,10,12,13,15,17,19,9,8,11,13,15,17,21,14,17,16,14,14,8,9,12,15,19,12,10,13,15,18,11
,13,15,16,10,11,7,21,9,14,18,19,14,9,11,15,20,20,18,15,16.
Null hypothesis: there is no significance difference between two mean no. of tomatoes
per plant in both the varieties.
SOLUTION:

13. x1 f1 f1x1
6 2 36 72 12
7 2 49 98 14
8 4 64 256 32
9 4 81 324 36
10 4 100 400 40
11 3 121 363 33
12 5 144 720 60
13 8 169 1352 104
14 7 196 1372 98
15 4 225 900 60
x1 f1 f1x1
6 2 36 72 12
7 2 49 98 14
8 4 64 256 32
9 4 81 324 36
10 4 100 400 40
11 3 121 363 33
12 5 144 720 60
13 8 169 1352 104
14 7 196 1372 98
15 4 225 900 60
Variety A: X1=∑f1x1/∑f1 = 604/50 =
12.08
=
=
=
= 9.03

14. Variety B:
x2 f2 x2f2
7 1 49 49 7
8 3 64 192 24
9 4 81 324 36
10 3 100 300 30
11 4 121 484 44
12 3 144 432 36
13 4 169 676 52
14 5 196 980 70
15 7 225 1575 105
16 3 256 768 48
17 3 289 867 51
18 3 324 972 54
19 3 361 1083 57
20 2 400 800 40
21 2 441 882 42
Total 10384 696
x2 f2 x2f2
7 1 49 49 7
8 3 64 192 24
9 4 81 324 36
10 3 100 300 30
11 4 121 484 44
12 3 144 432 36
13 4 169 676 52
14 5 196 980 70
15 7 225 1575 105
16 3 256 768 48
17 3 289 867 51
18 3 324 972 54
19 3 361 1083 57
20 2 400 800 40
21 2 441 882 42
Total 10384 696
2
= 696/50
= 13.92
=
=
=13.91

15. Sd =
Sd =
Sd =
9.03+13.91
50
Sd = 0.45
Sd = 0.67
t =
x1-x2
Sd
t =
12.08-13.92
0.67
t =
-1.84
0.67
t = 2.74
Conclusion : the calculated value of t is 2.74 greater than the
tabulated value (2.71) for 98 or 120 degree of freedom at 1% level of
significance. Hence there is no significance difference between two
Degree of freedom = 50+50-2= 100-2 = 98= (n1+n2-2)

17. t-TEST FOR TWO SMALL SAMPLES:
 Sample consisting of upto 30 observations or items is
called as small samples.
t =
x1-x2
Sd
1/n1+1/n2
or t =
x1-x2
Sd
n1n2
n1+n2
Where,
• X1 = mean of first sample =
X2 = mean of second sample=
or
oror
or
• n1=number of observation in the first sample
n2= number of observation in the second sample

18. Where,
• Sd =Standard error of the difference ,Sd =
S1
2
= varience of first sample =
S2
2
= varience of second sample =
 Degrees of freedom= (n1+n2-2)
)
)
2
Pooled standard
deviation or standard
= error of difference:
)
+
)
2
)
)
+
n1+n2-2
=

19.  Degrees of freedom= (n1+n2-2)
)
)
+
n1+n2-2
=Sd

20. EXAMPLE-1:
Q . in a mutation breeding experiments, gamma irradiation effect was evaluated on 100
seed weight in grams per plant of a mungbean variety in M2 generation. The
experimeters obtained the following results .analyse the data using the t-test and give
your inference as regards the effect of gamma irradiation.
Control 2.9 3.1 3.5 3.4 3 4 3.7 3 4 4
Treated 2.7 2.8 3 3.5 3.7 3.2 3 3.1 2.9 2.8
SOLUTION:
Null hypothesis: there is no significance difference between the mean 100 seed weigth
per plant in the control and treatment.

21. Control Treated
x1 x1
2
x2 x2
2
2.9 8.41 2.7 7.29
3.1 9.61 2.8 7.84
3.5 12.25 3 9
3.4 11.56 3.5 12.25
3 9 3.7 13.69
4 16 3.2 10.24
3.7 13.69 3 9
3 9 3.1 9.61
4 16 2.9 8.41
4 16 2.8 7.84
∑x1=34.6 ∑x1
2
=121.52 ∑x2=30.7 ∑x2
2
=95.17X1 =
=
34.6
10
= 3.46
X2
==
30.7
10
= 3.07

22. )
)
+
n1+n2-2
=Sd
)
+
10+10-2
=Sd
+
18
=Sd

23. +
18
=Sd
-119.71
+
18
=Sd
18
=Sd
=Sd
=Sd 0.38
t =
x1-x2
Sd
n1n2
n1+n2
t = 3.46-3.07
0.38
10*10
10+10
t =
0.39
0.38
100
20
t = 1.02 5
t = 1.02*2.23
t =
2.27

24. Degrees of freedom= (n1+n2-2) = 10+10-2
=18
Conclusion:
The calculated value of t(2.27) is less than the tabulated value (2.87) for
18 degree of freedom at 1% level of significance. hence the null
hypothesis stating that there is no significance difference between the two
seed weigth of plant get accepted at P=0.01

25. T-TEST FOR PAIRED SAMPLES:
Tests the mean of one group twice.
Examples:
 Testing the balance before and after drinking.
 Testing IQ level before and after the training program.
d√n
Sd
t=ort= d
SEd
Where:
d =
∑d
n
SEd = Standard error of the difference
Sd = Standard deviation of the differnce=
∑d2
-(∑d)2
n
n-1
Sd
=
= Sd
√n
Degree of freedom,d.f.= n-1
d = the mean of the difference between the paired values.,

26. EXAMPLE-1:
Q. Data recorded on the rainfall at two places , A and B in 10years given below.
Analyse the data and darw your inferences whether the two places have the same
mean annual rainfall.
Years Rainfall in mm at A Rainfall in mm at B
1971 177.29 69.79
1972 146.12 103.93
1973 159.89 74.29
1974 111.68 123.21
1975 96.94 91.47
1976 120.41 68.18
1977 114.95 55.50
1978 114.14 105.20
1979 137.38 101.88
1980 119.42 121.84

27. SOLUTION:
Null hypothesis:H0 : There is no significance difference in the rainfall of the two
places A and B.
Years Rainfall in
mm at A
Rainfall in
mm at B
Differece
x1-x2=d
d2
1971 177.29 69.79 107.50 11556.25
1972 146.12 103.93 42.19 1779.99
1973 159.89 74.29 85.60 7327.36
1974 111.68 123.21 -11.53 132.94
1975 96.94 91.47 5.47 29.92
1976 120.41 68.18 52.23 2727.97
1977 114.95 55.50 59.45 3534.30
1978 114.14 105.20 8.94 79092
1979 137.38 101.88 35.50 1260.25
1980 119.42 121.84 -2.42 5.86
Total _ _ ∑d=382.93 ∑d2
=28434.76

28. d =
∑d
n
∑d2
-(∑d)2
n
n-1
28434.76-(382.93)2/10
10-1
28434.7-146635.38/10
9
28434.7-14663.53
9
13771.22
9
1530.14
39.12
=38.29
= 382.92
10
Sd
=
Sd
=
Sd
=
Sd
=
Sd
=
Sd
=
Sd
=

29. d√n
Sd
38.29√10
39.12
38.29*3.16
39.12
120.99
39.12
3.10
Degree of freedom= n-1 = 10-1 =9
Since the calculated t value (3.10) is less then the tabulated t value (3.25) for
90
of freedom at 1% level of significance. It is clearly indicates thet the two
means of rain fall at two places are very much similar hence the null
hypothesis stating that there is no significance difference in the rainfall of the
two places A and B get accepted at P=0.010 .
t=
t=
t=
t=
t=

31. A QUICK
REVIEW

32. t-test type Paired large samples small samples
What it is?? Tests the mean
of one group
twice.
Sample
consisting of
more than 30
observations or
items is called as
large samples.
Sample consisting of upto 30
observations or items is called as
small samples.
Formula of t
Formula for
standard deviation
of difference
Formula for
varience S2
______
Formula for mean
Degree of freedom
d.f.
n-1
d√n
Sd
t= t =
x1-x2
Sd
t =
x1-x2
Sd
n1n2
n1+n2
Sd =
Sd = Sd = Sd =
∑d2
-(∑d)2
n
n-1
)
S2
=
S2
=
)
d =
∑d
n
X = X=
(n1+n2-2) (n1+n2-2)

33. THANK YOU