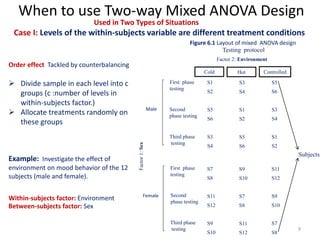
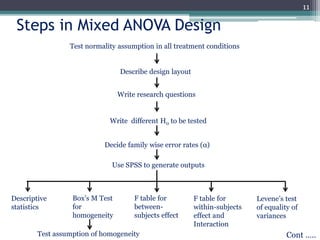
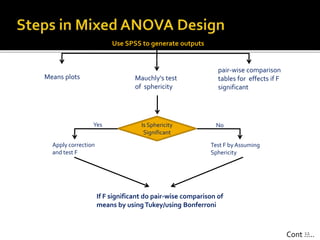
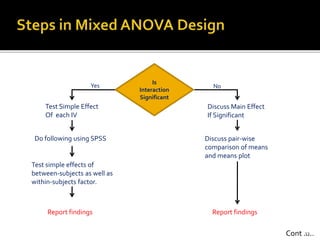
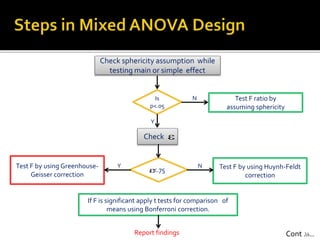
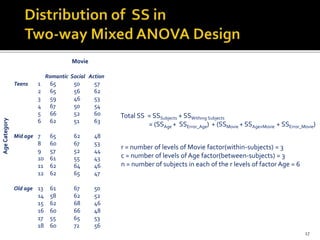
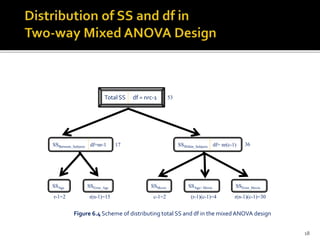
The document presents an overview of split plot design and two-way mixed ANOVA, focusing on the effects of between-subjects and within-subjects factors on dependent variables in various research contexts. It details methodologies for investigating interactions, the use of placebo effects, and the appropriate statistical tests, along with practical examples across different fields. The work serves as a guide on design layout, statistical assumptions, and reporting findings in experimental research.

1. Presented by
Dr.J.P.Verma
MSc (Statistics), PhD, MA(Psychology), Masters(Computer Application)
Professor(Statistics)
Lakshmibai National Institute of Physical Education, Gwalior, India
(Deemed University)
Email: vermajprakash@gmail.com

2. Split plot design
Also known as
In a situation where the effect of two factors (one between-subjects and
another within-subjects) on some dependent variable is investigated.
When to Use
2

3.  Subjects are assigned to treatment conditions by using
randomization and repeated measures concept.
 Different treatments of within-subject factor are randomly assigned
to the subjects in each level of the between-subjects factor.
 All subjects in each level of the between-subjects factor are tested
in each treatment condition of the within-subject factor.
 To test the differences between two or more independent groups
while subjects are repeatedly measured on some dependent
variable in each level of the within-subject factor.
Purpose
Features
3

4. Objective To investigate the effect of time of testing on memory
retention among boys and girls.
Gender : Between-subjects factor Levels: male and female
Time : Within-subjects factor Levels: morning, afternoon and evening
Purpose of using this design To check interaction
What Interaction means ? Whether pattern of the memory retention during
different testing time differs in male and female
4

5. 5
This Presentation is based on
Chapter 6 of the book
Repeated Measures Design
for Empirical Researchers
Published by Wiley, USA
Complete Presentation can be accessed on
Companion Website
of the Book

6. Subjects are
randomly divided
Experimental
group
Control group
Pre
testing
Post
testing
Treatment
Pre
testing
Post
testing
Placebo
 Subjects think that they are a part of experiment
 Subjects Don’t know whether they are in experimental or control group hence bias reduction
Purpose of Placebo
Pre-post design can be
solved by using two-
way mixed ANOVA
But better
way is
To use ANCOVA design
6

7.  Interaction between within-subjects and between-subjects factors
can be investigated.
 Between-subjects factor can be considered as a covariate.
 This design is efficient in comparison to single factor RMD because
between-subjects factor reduces error variance substantially.
 The design is very sensitive in detecting even the slightest variation
in the groups.
 In mixed ANOVA design post-hoc test can be applied for between-
subjects factor.
7

8. 1. A human resource manager may investigate the effect of training
intervention (onsite, offsite and mix of these two) on learning skills for
their employees (male and female).
2. A psychologist may like to investigate the effect of cognitive therapy
(three different types) on the stress level. Here sex may be taken as
between-subjects factor.
3. An educational psychologists may investigate the effect of learning
methods (traditional, audio-visual and self learning) and IQ(high and low)
on memory retention.
4. A basketball coach may wish to investigate the effect of distance (3 mt., 4
mt and 5 mt.) and gender on shooting performance in basketball. Here
distance is a within-subjects and gender is a between-subjects factor
respectively.
5. A nutritionist may be interested to compare the effect of three diet
programmes on weight reduction in a six week experiment. Subjects may
be in different active, semi-active and sedentary groups.
8

9. Factor 2: Environment
S1
S2
S5
S6
S3
S4
Controlled
S3
S4
S1
S2
S5
S6
S5
S6
S3
S4
S1
S2
Testing protocol
HotCold
S7
S8
S11
S12
S9
S10
S9
S10
S7
S8
S11
S12
S11
S12
S9
S10
S7
S8
Subjects
Factor1:Sex
First phase
testing
Second
phase testing
Third phase
testing
Male
Female
First phase
testing
Second
phase testing
Third phase
testing
Figure 6.1 Layout of mixed ANOVA design
Case I: Levels of the within-subjects variable are different treatment conditions
When to use Two-way Mixed ANOVA Design
Used in Two Types of Situations
Order effect Tackled by counterbalancing
 Divide sample in each level into c
groups (c :number of levels in
within-subjects factor.)
 Allocate treatments randomly on
these groups
Example: Investigate the effect of
environment on mood behavior of the 12
subjects (male and female).
Within-subjects factor: Environment
Between-subjects factor: Sex
9

10. 2 weeks
S1
S2
S3
S4
S5
S1
S2
S3
S4
S5
S1
S2
S3
S4
S5
4 weeks 6 weeks
Factor 2: Time
Initial
S1
S2
S3
S4
S5
Male
Female
Subjects
S6
S7
S8
S9
S10
Testing protocol
S6
S7
S8
S9
S10
S6
S7
S8
S9
S10
S6
S7
S8
S9
S10
Factor1:Sex
Figure 6.2 Layout of mixed ANOVA design
Case II: levels of the within-subjects variable are different time periods
When to use Mixed ANOVA Design
Used inTwoTypes of Situations
Example: To investigate the effect of
Time on the effectiveness of an exercise
therapy programme organized on 5
male and 5 female participants.
10

11. Steps in Mixed ANOVA Design
Test normality assumption in all treatment conditions
Describe design layout
Write research questions
Write different H0 to be tested
Decide family wise error rates (α)
Use SPSS to generate outputs
Descriptive
statistics
F table for
within-subjects
effect and
Interaction
Cont …..
Box’s M Test
for
homogeneity
Levene’s test
of equality of
variances
Test assumption of homogeneity
F table for
between-
subjects effect
11

12. Is Sphericity
Significant
No
Test F by Assuming
Sphericity
If F significant do pair-wise comparison of
means by usingTukey/using Bonferroni
Yes
Apply correction
and test F
Use SPSS to generate outputs
Means plots
Cont …..
pair-wise comparison
tables for effects if F
significant
Mauchly's test
of sphericity
12

13. Do following using SPSS
Is
Interaction
Significant
No
Discuss Main Effect
If Significant
Discuss pair-wise
comparison of means
and means plot
Yes
Test Simple Effect
Of each IV
Test simple effects of
between-subjects as well as
within-subjects factor.
Report findings Report findings
Cont …..13

14. Check sphericity assumption while
testing main or simple effect
Is
p<.05
Test F ratio by
assuming sphericity
N
Y
Check 
<.75 Test F by using Huynh-Feldt
correction
NTest F by using Greenhouse-
Geisser correction
Y
If F is significant apply t tests for comparison of
means using Bonferroni correction.
Report findings Cont …..14

15. Movie
Romantic Social Action
Teens 1 65 50 57
2 65 56 62
3 59 46 53
4 67 50 54
5 66 52 60
6 62 51 63
Mid age 7 65 62 48
8 60 67 53
9 57 52 44
10 61 55 43
11 62 64 46
12 62 65 47
Old age 13 61 67 50
14 58 62 52
15 62 68 46
16 60 66 48
17 55 65 53
18 60 72 56
AgeCategory
To investigate the effect of age and movie
types on the enjoyment of audience.
Objective
Age category :Teens, Mid age and Old age
Movie type : Romantic, Social and Action
Table 6.1 Score on enjoyment reported by the
subjects after watching movies 15

16. S1
S2
S5
S6
S3
S4
Action
First testing
Second testing
Third testing
SocialRomantic
Teens
Subjects
S3
S4
S1
S2
S5
S6
S5
S6
S3
S4
S1
S2
S7
S8
S11
S12
S9
S10
First testing
Second testing
Third testing
Mid Age
S9
S10
S7
S8
S11
S12
S11
S12
S9
S10
S7
S8
S13
S14
S17
S18
S15
S16
First testing
Second testing
Third testing
OldAge
S15
S16
S13
S14
S17
S18
S17
S18
S15
S16
S13
S14
Factor1:Age
Factor 2: Movie
Testing protocol
Figure 6.3 Layout of the mixed ANOVA design in the
illustration
16

17. r = number of levels of Movie factor(within-subjects) = 3
c = number of levels of Age factor(between-subjects) = 3
n = number of subjects in each of the r levels of factor Age = 6
Movie
Romantic Social Action
Teens 1 65 50 57
2 65 56 62
3 59 46 53
4 67 50 54
5 66 52 60
6 62 51 63
Mid age 7 65 62 48
8 60 67 53
9 57 52 44
10 61 55 43
11 62 64 46
12 62 65 47
Old age 13 61 67 50
14 58 62 52
15 62 68 46
16 60 66 48
17 55 65 53
18 60 72 56
AgeCategory
Total SS = SSSubjects + SSWithing Subjects
= (SSAge + SSError_Age) + (SSMovie + SSAge×Movie + SSError_Movie)
17

18. SSBetween_Subjects df=nr-1
Total SS df = nrc-1
SSWithin_Subjects df= nr(c-1)
53
17 36
SSError_AgeSSAge SSAge× MovieSSMovie SSError_Movie
r-1=2 r(n-1)=15 c-1=2 (r-1)(c-1)=4 r(n-1)(c-1)=30
Figure 6.4 Scheme of distributing total SS and df in the mixed ANOVA design
18

19.  Whether enjoyment in watching movie depends upon the age of the subjects.
 Whether enjoyment in watching movie depends upon the type of movie seen
by the subject.
 Whether interaction between age and movie type affects the enjoyment in
watching movie.
against H1:At least one group mean differs
Research Questions
Hypotheses Construction
Effect of Movie
against H1: At least one group mean differs
Effect of Age
Interaction Effect (Age × Movie)
H0:There is no interaction betweenAge and Music
against H1:The interaction betweenAge and Music is significant
ActionSocialRomantic0 :H 
age_Oldage_MidTeens0:H 
19

20. Bonferroni correction shall be used for
correcting level of significance for pair
wise comparison of means
Family wise error rate(α) is .05
In case interaction is significant multipleANOVA (independent and repeated)
shall be done to test the simple effect.
α for testing significance of F in simple effect would
be .017(=.05/3) level.
20

21. Figure 6.5 Data format in the two-way mixed ANOVA design
21

22. Analyze General Linear Model Repeated Measures
Figure 6.5 Screen for initiating commands for the two-way mixedANOVA design
While being in DataView click on the following command sequence
22

23. 23
To buy the book
Repeated Measures Design
for Empirical Researchers
and all associated presentations
Click Here
Complete presentation is available on
companion website of the book