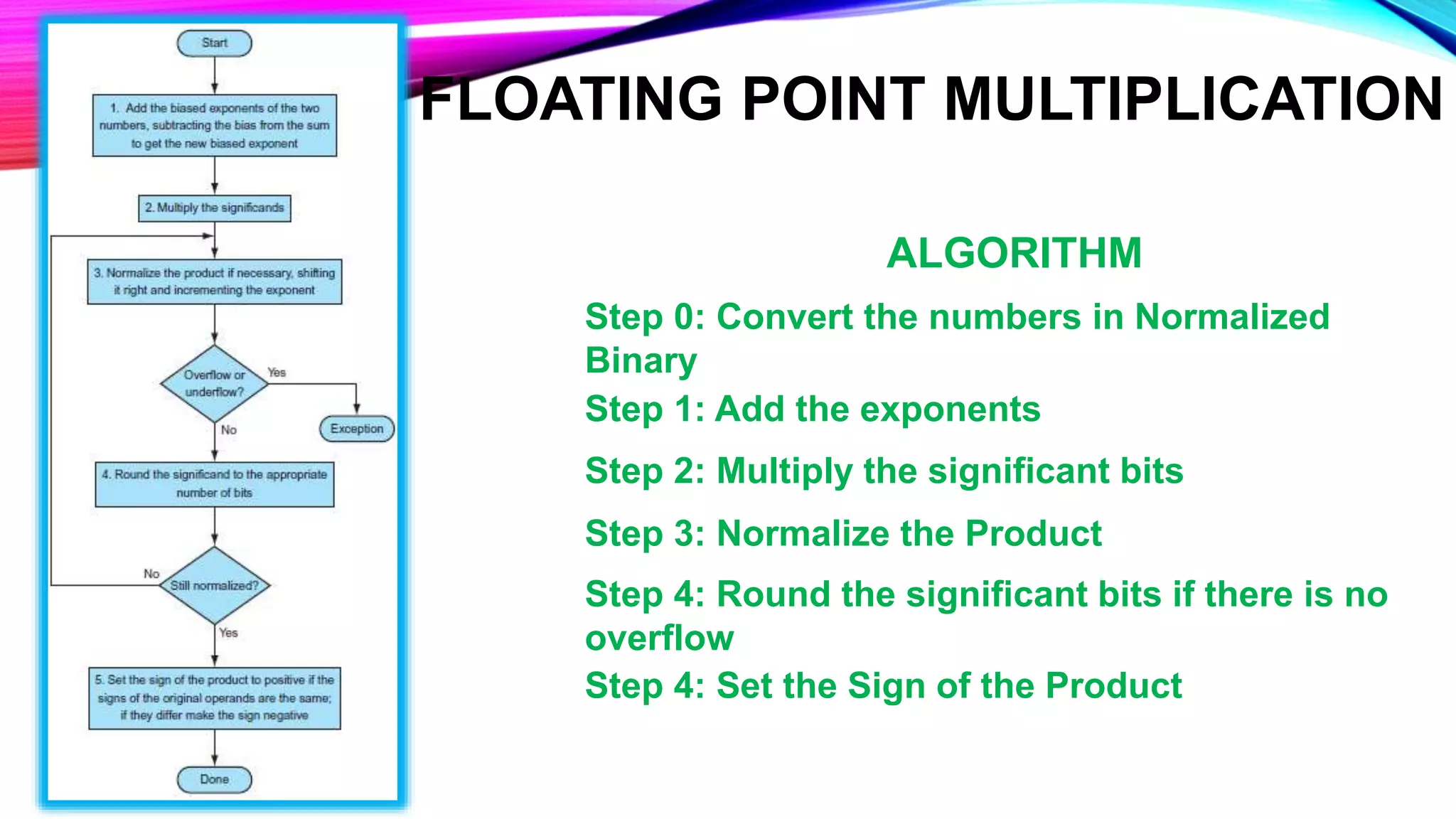
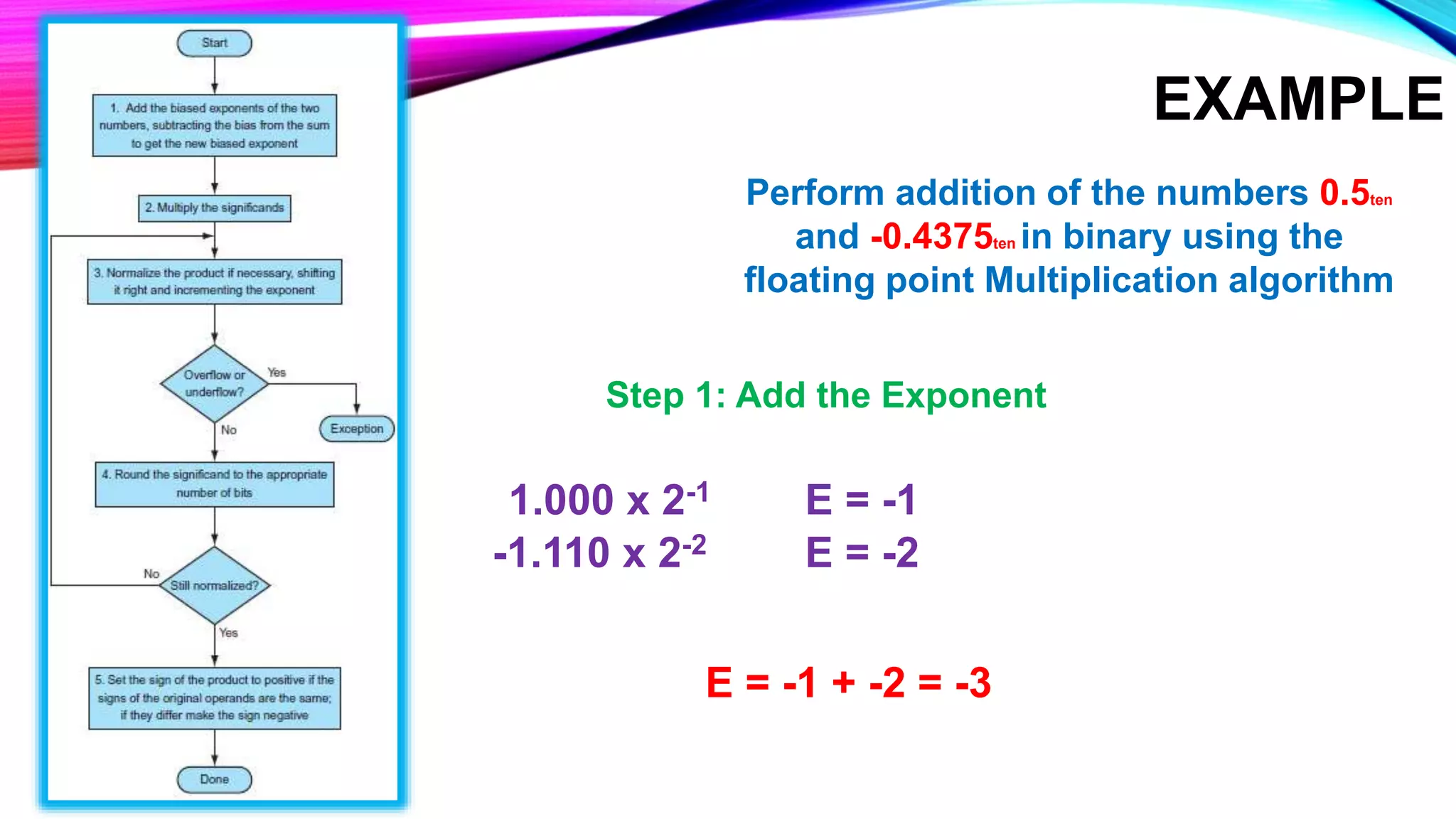
The document describes the floating point multiplication algorithm in 5 steps: 1) Convert the numbers to normalized binary representation. 2) Add the exponents. 3) Multiply the significant bits. 4) Normalize the product and round the significant bits if needed. 5) Set the sign of the product. It then provides an example of multiplying 0.5 and -0.4375 in binary using this algorithm.

1. FLOATING POINT
MULTIPLICATION
Mr. C.KARTHIKEYAN,
ASSISTANT PROFESSOR,
ECE , RMKCET

2. FLOATING POINT MULTIPLICATION
ALGORITHM
Step 0: Convert the numbers in Normalized
Binary
Step 1: Add the exponents
Step 2: Multiply the significant bits
Step 3: Normalize the Product
Step 4: Round the significant bits if there is no
overflow
Step 4: Set the Sign of the Product

3. EXAMPLE
Perform addition of the numbers 0.5ten
and -0.4375ten in binary using the
floating point Multiplication algorithm
Step 0: Convert to Normalized Binary
Binary Representation
0.5 x 2 = 1.0 1
0.75 x 2 = 1.50 1
0.50 x 2 = 1.00 1
0.875 x 2 = 1.75 1
0.4375 x 2 = 0.875 0
Binary Representation
0.510 = 0.12
0.437510 = 0.01112
+1.000 x 2-1
-1.110 x 2-2

4. Step 1: Add the Exponent
1.000 x 2-1
-1.110 x 2-2
E = -1
E = -2
E = -1 + -2 = -3
Perform addition of the numbers 0.5ten
and -0.4375ten in binary using the
floating point Multiplication algorithm
EXAMPLE

5. EXAMPLE
Step 2: Multiply the Significant
1.000 x 2-1
-1.110 x 2-2
1.000
1.110 (+)
1.110000 1.110000 x 2-3
Perform addition of the numbers 0.5ten
and -0.4375ten in binary using the
floating point Multiplication algorithm

6. EXAMPLE
Step 3: Normalization
(-1)S x 1.F x 2E
1.110000 x 2-3
1.110000 x 2-3
Perform addition of the numbers 0.5ten
and -0.4375ten in binary using the
floating point Multiplication algorithm

7. EXAMPLE
Step 4: Rounding
1.110000 x 2-3
G R S Rounding Action
0 0 0 Truncate
0 0 1 Truncate
0 1 0 Truncate
0 1 1 Truncate
1 0 0 Round to Even
1 0 1 Round Up
1 1 0 Round Up
1 1 1 Round Up
GUARD
BIT(G)
ROUND
BIT(R)
STICKY BITS
(S)
1.110 x 2-3
Perform addition of the numbers 0.5ten
and -0.4375ten in binary using the
floating point Multiplication algorithm
1.110000 x 2-3

8. EXAMPLE
Step 5: Set the Sign
1.110 x 2-3
Perform addition of the numbers 0.5ten
and -0.4375ten in binary using the
floating point Multiplication algorithm
-1.110 x 2-3