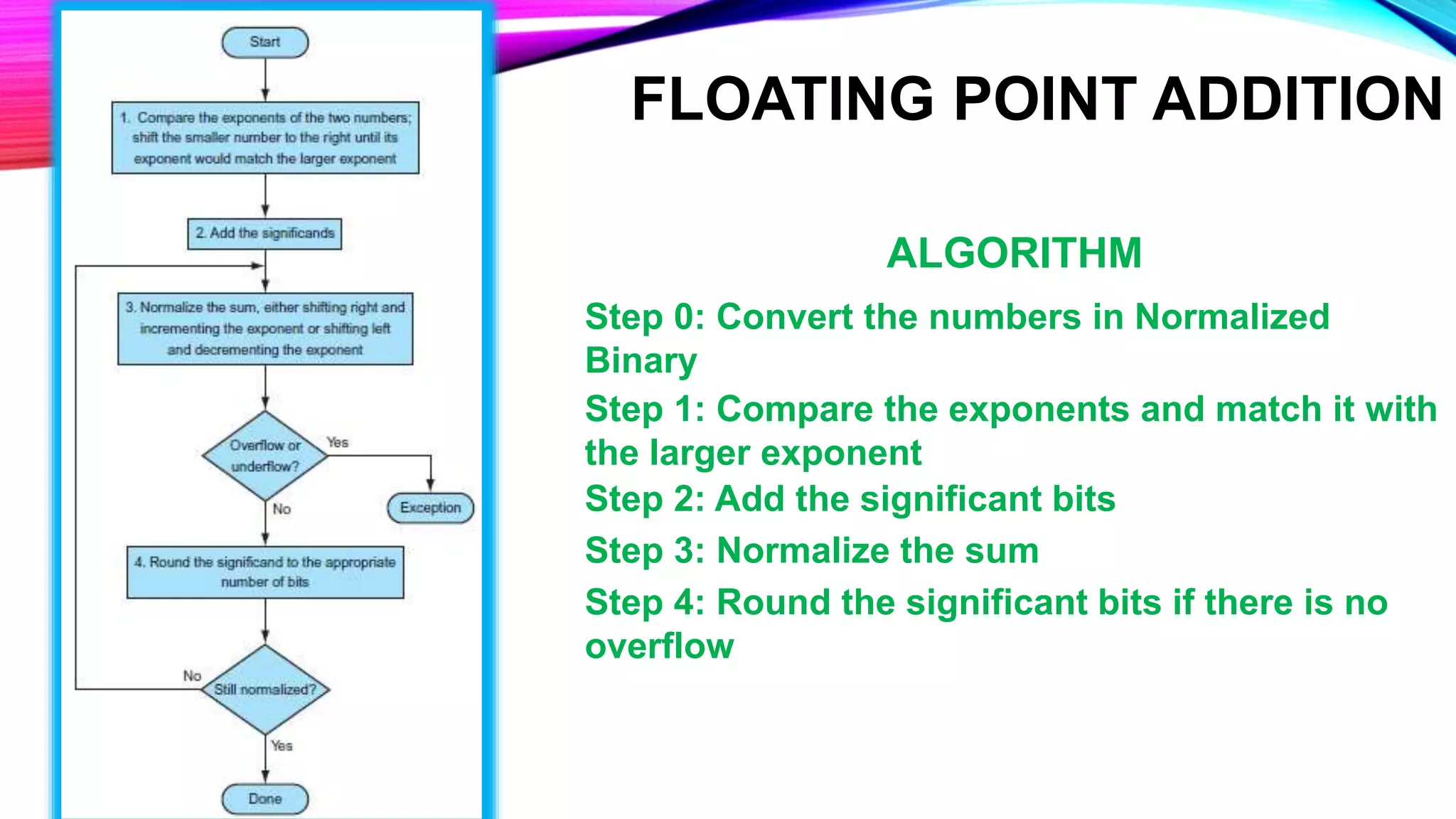
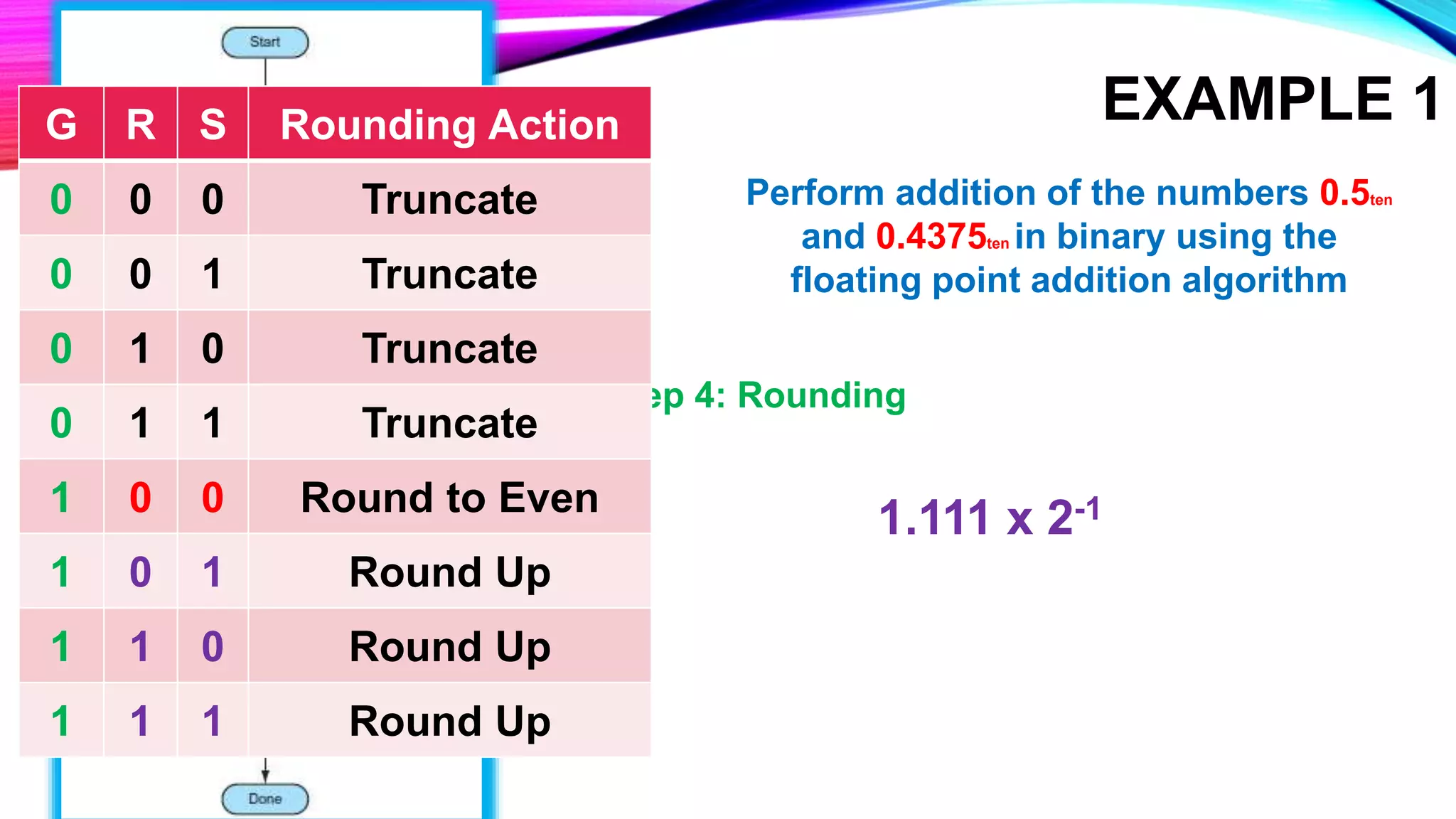
This document describes the floating point addition algorithm and provides two examples of performing floating point addition in binary. The algorithm involves 4 steps: 1) Convert the numbers to normalized binary, 2) Compare the exponents and match the larger one, 3) Add the significant bits, and 4) Normalize and round the sum if needed. The examples show applying this algorithm to add 0.5 and 0.4375, yielding 0.9375, and to add 10.01101 x 21 and 0.00101101 x 22, yielding 1.01100001 x 22.

1. FLOATING POINT ADDITION
Mr. C.KARTHIKEYAN,
ASSISTANT PROFESSOR,
ECE , RMKCET

2. FLOATING POINT ADDITION
ALGORITHM
Step 0: Convert the numbers in Normalized
Binary
Step 1: Compare the exponents and match it with
the larger exponent
Step 2: Add the significant bits
Step 3: Normalize the sum
Step 4: Round the significant bits if there is no
overflow

3. EXAMPLE 1
Perform addition of the numbers 0.5ten
and 0.4375ten in binary using the
floating point addition algorithm
Step 0: Convert to Normalized Binary
Binary Representation
0.5 x 2 = 1.0 1
0.75 x 2 = 1.50 1
0.50 x 2 = 1.00 1
0.875 x 2 = 1.75 1
0.4375 x 2 = 0.875 0
Binary Representation
0.510 = 0.12
0.437510 = 0.01112
1.000 x 2-1
1.110 x 2-2

4. EXAMPLE 1
Perform addition of the numbers 0.5ten
and 0.4375ten in binary using the
floating point addition algorithm
Step 1: Exponent Comparison
1.000 x 2-1
1.110 x 2-2
1.000 x 2-1
1.110 x 2-2
1.000 x 2-1
0.111 x 2-1

5. EXAMPLE 1
Perform addition of the numbers 0.5ten
and 0.4375ten in binary using the
floating point addition algorithm
Step 2: Addition 1.000 x 2-1
0.111 x 2-1
1.000
0.111 (+)
1.111
1.111 x 2-1

6. EXAMPLE 1
Perform addition of the numbers 0.5ten
and 0.4375ten in binary using the
floating point addition algorithm
Step 3: Normalization
1.111 x 2-1
1.111 x 2-1
(-1)S x 1.F x 2E

7. EXAMPLE 1
Perform addition of the numbers 0.5ten
and 0.4375ten in binary using the
floating point addition algorithm
Step 4: Rounding
1.111 x 2-1
G R S Rounding Action
0 0 0 Truncate
0 0 1 Truncate
0 1 0 Truncate
0 1 1 Truncate
1 0 0 Round to Even
1 0 1 Round Up
1 1 0 Round Up
1 1 1 Round Up

8. EXAMPLE 1
Perform addition of the numbers 0.5ten
and 0.4375ten in binary using the
floating point addition algorithm
Final Answer
1.111 x 2-1 = 0.1111
0.937510

9. EXAMPLE 2
Perform addition of the numbers 10.01101 x 21
and 0.00101101 x 22 in binary using the
floating point addition algorithm
Step 0: Convert to Normalized Binary
10.01101 x 21 0.00101101 x 22
1.001101 x 22 1.01101 x 2-1

10. EXAMPLE 2
Perform addition of the numbers 10.01101 x 21
and 0.00101101 x 22 in binary using the
floating point addition algorithm
1.001101 x 22
1.01101 x 2-1
Step 1: Exponent Comparison
0.00101101 x 22

11. EXAMPLE 2
Perform addition of the numbers 10.01101 x 21
and 0.00101101 x 22 in binary using the
floating point addition algorithm
1.001101 x 22
0.00101101 x 22
Step 2: Addition
1.001101
0.00101101 (+)
1.01100001 1.01100001 x 22

12. EXAMPLE 2
Perform addition of the numbers 10.01101 x 21
and 0.00101101 x 22 in binary using the
floating point addition algorithm
Step 3: Normalization
1.01100001 x 22

13. EXAMPLE 2
Perform addition of the numbers 10.01101 x 21
and 0.00101101 x 22 in binary using the
floating point addition algorithm
Step 4: Rounding
1.01100001 x 22
G R S Rounding Action
0 0 0 Truncate
0 0 1 Truncate
0 1 0 Truncate
0 1 1 Truncate
1 0 0 Round to Even
1 0 1 Round Up
1 1 0 Round Up
1 1 1 Round Up
1.01100001 x 22
GUARD
BIT(G)
ROUND
BIT(R)
STICKY BITS
(S)
1.011 x 22