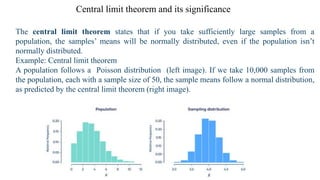
The document discusses various concepts of convergence in probability theory, including almost sure convergence, convergence in mean, convergence in probability, and convergence in distribution. It also explains the Central Limit Theorem, emphasizing that the sampling distribution of the mean is normally distributed as long as the sample size is sufficiently large (n ≥ 30) and other conditions are met. Additionally, it provides examples and solutions to illustrate these concepts.

1. UNIT 4

2. Almost Sure Convergence
Consider a sequence of random variables 𝑋1, 𝑋2, 𝑋3, ⋯⋯ that is defined on an
underlying sample space S. For simplicity, let us assume that S is a finite set, so
we can write
S={𝑠1,𝑠2,⋯,𝑠𝑘}.
Remember that each 𝑋𝑛 is a function from S to the set of real numbers. Thus, we
may write
Xn(si)=xni, for i=1,2,⋯,k.
After this random experiment is performed, one of the 𝑠𝑖's will be the outcome of
the experiment, and the values of the 𝑋𝑛's are known. If 𝑠𝑗 is the outcome of the
experiment, we observe the following sequence:
x1j, x2j, x3j,⋯.

3. Example:
Consider the following random experiment: A fair coin is tossed once.
Here, the sample space has only two elements S={H,T}𝑆={𝐻,𝑇}. We
define a sequence of random variables X1𝑋1, X2𝑋2, X3𝑋3, ⋯⋯ on this
sample space as follows:
Xn(s) = n/n+1 if s=H
(−1)n if s=T
a.For each of the possible outcomes (H or T), determine whether the
resulting sequence of real numbers converges or not.
b.Find P({si∈S:lim n→∞Xn(si)=1}).

4. Solution a.
If the outcome is H, then we have Xn(H)=n/n+1, so we obtain the following
sequence
1/2,2/3,3/4,4/5,⋯.
This sequence converges to 1 as n goes to infinity. If the outcome is T, then we
have
Xn(T) = (−1)n,
so we obtain the following sequence
−1,1,−1,1,−1,⋯.

5. b) By part (a), the event
{si ∈S :lim n→∞ Xn(si)=1
happens if and only if the outcome is H, so
P({si ∈ S: limn→∞ Xn(si)=1})=P(H)=1/2.

6. Convergence in Mean

7. Convergence in the mean square sense, also known as
convergence in the mean squared error (MSE), is a concept
commonly encountered in statistics and probability theory,
particularly in the context of parameter estimation. It refers to the
behavior of an estimator as the sample size increases indefinitely.
An estimator is said to converge in the mean square sense if, as the
sample size grows large, the expected squared difference between
the estimator and the true parameter converges to zero.

8. Convergence in Mean
Let 𝑟≥1 be a fixed number. A sequence of random variables 𝑋1, 𝑋2,
𝑋3, ⋯⋯ converges in the 𝑟th mean or in the 𝐿𝑟 norm to a random
variable 𝑋, shown by 𝐿𝑟
𝑋𝑛 → 𝑋, if
limn→∞E(|Xn−X|r)=0.
If 𝑟=2, it is called the mean-square convergence, and it is shown
by
𝑚.𝑠.
𝑋𝑛 → 𝑋.

9. Example
Let Xn∼Uniform (0,1/n) Show that 𝐿𝑟
𝑋𝑛 → 0, for any 𝑟≥1.
•Solution
•The PDF of 𝑋𝑛 is given by
fXn(x)= 𝑛 0≤𝑥≤1
0 otherwise
We have
E(|Xn−0|r) = ∫1/n
0 xrn dx
= {1/(r+1)nr }→0, for all r≥1.

10. Convergence in Probability
Convergence in probability is stronger than convergence in
distribution. In particular, for a sequence X1, X2, X3, ⋯⋯ to
converge to a random variable X, we must have
that P(|Xn−X|≥ϵ) goes to 0 as n→∞, for any ϵ>0.
To say that Xn converges in probability to X, we write
Xn →p X
Here is the formal definition of convergence in probability:

11. Convergence in Probability
A sequence of random variables X1, X2, X3, ⋯⋯ converges in
probability to a random variable X, shown by p
Xn → X, if
limn→∞P(|Xn−X|≥ϵ)=0, for all ϵ>0.

12. Example:
Let Xn ∼ Exponential(n),
p
show that Xn→0.
That is, the sequence X1, X2, X3, ⋯⋯ converges in probability to the zero random
variable X.
Solution: We have
Lim n→∞P(|Xn−0|≥ϵ) =limn→∞P(Xn ≥ ϵ) ( since Xn≥0)
=limn→∞e−nϵ ( since Xn∼ Exponential(n) )
=0, for all ϵ>0.

13. Convergence in Distribution
Convergence in distribution is in some sense the weakest type of
convergence. All it says is that the CDF of 𝑋𝑛's converges to the CDF
of 𝑋 as 𝑛 goes to infinity. It does not require any dependence between
the 𝑋𝑛's and 𝑋. We saw this type of convergence before when we
discussed the central limit theorem. To say that 𝑋𝑛 converges in
distribution to 𝑋, we write 𝑑
𝑋𝑛 → 𝑋.
Here is a formal definition of convergence in distribution:

14. Convergence in Distribution
A sequence of random variables 𝑋1, 𝑋2, 𝑋3, ⋯⋯ converges in
distribution to a random variable 𝑋,
shown by 𝑑
𝑋𝑛 → 𝑋,
if lim𝑛→∞𝐹𝑋𝑛(𝑥)=𝐹𝑋(𝑥),
for all 𝑥 at which 𝐹𝑋(𝑥) is continuous.

15. Example
Let 𝑋2, 𝑋3,𝑋4, ⋯⋯ be a sequence of random variable such that
𝐹𝑋𝑛(𝑥) = 1−(1−1/𝑛)𝑛𝑥 𝑥>0
0 otherwise
Show that 𝑋𝑛 converges in distribution to 𝐸𝑥𝑝𝑜𝑛𝑒𝑛𝑡𝑖𝑎𝑙(1).
Let 𝑋∼𝐸𝑥𝑝𝑜𝑛𝑒𝑛𝑡𝑖𝑎𝑙(1). For 𝑥≤0, we have
𝐹𝑋𝑛(𝑥)=𝐹𝑋(𝑥)=0, for 𝑛=2,3,4,⋯.
For 𝑥≥0, we have
lim𝑛→∞𝐹𝑋𝑛(𝑥)=lim𝑛→∞(1−(1−1/𝑛)𝑛𝑥)
=1−lim𝑛→∞(1−1/𝑛)𝑛𝑥
=1−𝑒−𝑥
=𝐹𝑋(𝑥), for all 𝑥.
Thus, we conclude that 𝑑
𝑋𝑛 → 𝑋.

16. Central limit theorem and its significance
The central limit theorem states that if you take sufficiently large samples from a
population, the samples’ means will be normally distributed, even if the population isn’t
normally distributed.
Example: Central limit theorem
A population follows a Poisson distribution (left image). If we take 10,000 samples from
the population, each with a sample size of 50, the sample means follow a normal distribution,
as predicted by the central limit theorem (right image).

17. What is the central limit theorem?
The central limit theorem relies on the concept of a sampling distribution, which is the
probability distribution of a statistic for a large number of samples taken from a
population.
To understand sampling distributions:
•Suppose that you draw a random sample from a population and calculate a statistics for
the sample, such as the mean.
•Now you draw another random sample of the same size, and again calculate the mean.
•You repeat this process many times, and end up with a large number of means, one for
each sample.
The distribution of the sample means is an example of a sampling distribution.
The central limit theorem says that the sampling distribution of the mean will always
be normally distributed, as long as the sample size is large enough. Regardless of
whether the population has a normal, Poisson, binomial, or any other distribution, the
sampling distribution of the mean will be normal.

18. Central limit theorem formula
The parameters of the sampling distribution of the mean are determined by the parameters of the
population:
•The mean of the sampling distribution is the mean of the population.
•The standard deviation of the sampling distribution is the standard deviation of the population divided by
the square root of the sample size.
We can describe the sampling distribution of the mean using this notation:
Where:
•X̄ is the sampling distribution of the sample means
•~ means “follows the distribution”
•N is the normal distribution
•µ is the mean of the population
•σ is the standard deviation of the population
•n is the sample size

19. Sample size and the central limit theorem
The sample size (n) is the number of observations drawn from the population for each
sample. The sample size is the same for all samples.
The sample size affects the sampling distribution of the mean in two ways.
1. Sample size and normality
The larger the sample size, the more closely the sampling distribution will follow a normal
distribution.
When the sample size is small, the sampling distribution of the mean is sometimes non-
normal. That’s because the central limit theorem only holds true when the sample size is
“sufficiently large.”
By convention, we consider a sample size of 30 to be “sufficiently large.”
When n < 30, the central limit theorem doesn’t apply. The sampling distribution will follow a
similar distribution to the population. Therefore, the sampling distribution will only be
normal if the population is normal.
When n ≥ 30, the central limit theorem applies. The sampling distribution will approximately
follow a normal distribution.

20. 2. Sample size and standard deviations
The sample size affects the standard deviation of the sampling distribution.
Standard deviation is a measure of the variability or spread of the distribution
(i.e., how wide or narrow it is).
When n is low, the standard deviation is high. There’s a lot of spread in the
samples’ means because they aren’t precise estimates of the population’s
mean.
When n is high, the standard deviation is low. There’s not much spread in the
samples’ means because they’re precise estimates of the population’s mean.

21. Conditions of the central limit theorem
The central limit theorem states that the sampling distribution of the mean
will always follow a normal distribution under the following conditions:
The sample size is sufficiently large. This condition is usually met if the
sample size is n ≥ 30.
The samples are independent and identically distributed (i.i.d.) random
variables. This condition is usually met if the sampling is random.
The population’s distribution has finite variance. Central limit theorem
doesn’t apply to distributions with infinite variance, such as the Cauchy
distribution. Most distributions have finite variance.

22. References:
1. https://www.scribbr.com/statistics/central-limit-theorem
2. https://www.probabilitycourse.com/