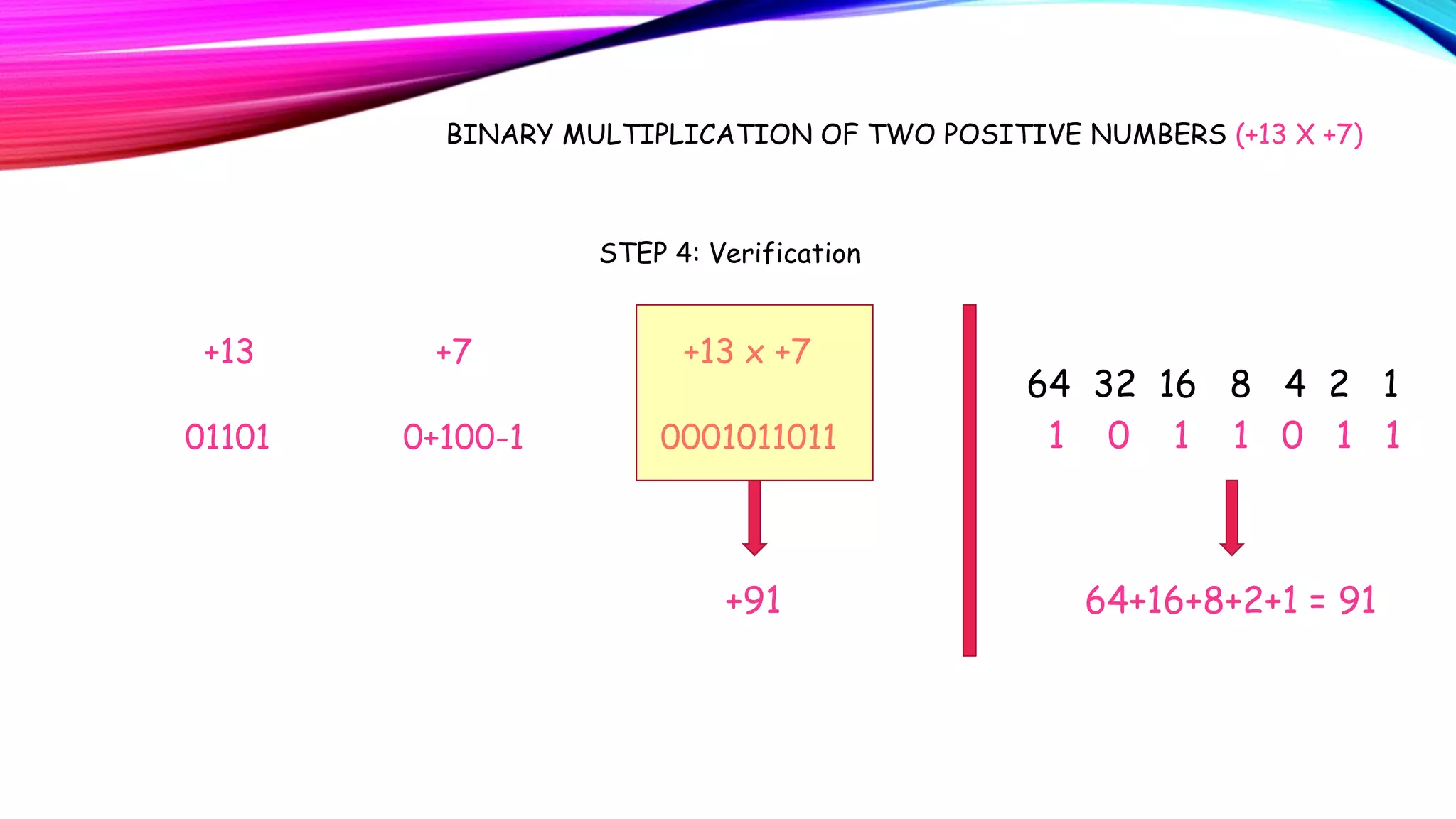
Booth's algorithm is a method for multiplying two binary numbers, including positive and negative numbers, by recoding the multiplier into {-1, 0, +1} and then multiplying the multiplicand by the recoded bits. For example, to multiply the positive numbers +13 and +7 in binary, the document shows recoding +7 as 0+1-1, multiplying +13 by each recoded bit, and adding the results to get the product of 91. The algorithm was created by Andrew Booth to speed up multiplication on early calculators.

1. BOOTH’S ALGORITHM
E.g.: Binary Multiplication of two Positive Numbers (+13 X +7)
Mr. C.KARTHIKEYAN,
ASSISTANT PROFESSOR,
ECE , RMKCET

2. BOOTH’S ALGORITHM
Booth's multiplication algorithm is used to multiply two signed binary numbers
in two's Complement notation.
The algorithm was invented by Andrew Donald Booth in 1950.
Booth used desk calculators that were faster at shifting than adding and created
the algorithm to increase their speed.
It handles both positive and negative multiplier uniformly.
Basic Understandings required to learn the topic are:
1. Binary Number Representation
2. Binary Multiplication

3. EXPLANATION WITH AN
EXAMPLE
Binary Multiplication of two Positive Numbers (+13 X +7)
STEP 1: Number Representation
Multiplicand +13
Multiplier +7
1101
111
0
0
0
Binary Representation 2’s Complement Representation
01101
00111

4. BINARY MULTIPLICATION OF TWO POSITIVE NUMBERS (+13 X +7)
STEP 2: Recoding of the Multiplier
Multiplier +7 00111
0 0 1 1 1
Recoded Multiplier
Multiplier
Multiplicand selected
Bit i Bit i-1
0 0 0 X Multiplicand
0 1 +1 X Multiplicand
1 0 -1 X Multiplicand
1 1 0 X Multiplicand
Booth’s Recoding Table
i
0
i-1
-1
0
i i-1
0
i i-1
+1
i i-1
0
i i-1

5. BINARY MULTIPLICATION OF TWO POSITIVE NUMBERS (+13 X +7)
STEP 3: Multiplication
Multiplicand 01101
Recoded Multiplier 0+100-1
Note:
1. Multiplication with 0 – 0 (00000)
2. Multiplication with +1 – Multiplicand (01101)
3. Multiplication with -1 – 2’s Complement of Multiplicand (10011)
0 1 1 0 1
0 +1 0 0 -1
1 0 0 1 1
1 1 1 1 1
0 0 0 0 0
0 0 0 0
0 0 0 0 0
0 0 0
0 1 1 0 1
0 0
0 0 0 0 0
0
1
1
0
1
1
0
1
1
1
0
1
0
1
0
1

6. BINARY MULTIPLICATION OF TWO POSITIVE NUMBERS (+13 X +7)
0001011011
+13 +7
01101 0+100-1
+13 x +7
1 0 1 1 0 1 1
64 32 16 8 4 2 1
64+16+8+2+1 = 91
+91
STEP 4: Verification