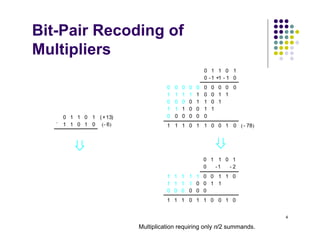
Bit-pair recoding is a technique that halves the maximum number of additions needed for multiplication by recoding the multiplier bits into pairs. It works by selecting the multiplicand (the number being multiplied) based on the values of bit pairs in the multiplier. For each bit pair, the selection table indicates which multiplicand (the regular value or the negative value) to use. This allows multiplication to be performed with only n/2 additions, where n is the number of bits in the multiplier.

1. 1
Fast Multiplication
Bit-Pair Recoding of Multipliers

2. 2
Bit-Pair Recoding of
Multipliers
Bit-pair recoding halves the maximum number of
summands (versions of the multiplicand).
1+1−
(a) Example of bit-pair recoding derived from Booth recoding
0
000
1 1 0 1 0
Implied 0 to right of LSB
1
0
Sign extension
1
21− −
−

3. 3
Bit-Pair Recoding of
Multipliers
i 1+ i 1
(b) Table of multiplicand selection decisions
selected at position i
MultiplicandMultiplier bit-pair
i
0
0
1
1
1
0
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
0
1
Multiplier bit on the right
0 0 ×M
1+
1
1+
0
1
2
2+
−
−
−
−
×M
×M
×M
×M
×M
×M
×M

4. 4
Bit-Pair Recoding of
Multipliers
1-
0000
1 1 1 1 1 0
0 0 0 0 11
1 1 1 1 10 0
0 0 0 0 0 0
0000 111111
0 1 1 0 1
0
1 010011111
1 1 1 1 0 0 1 1
0 0 0 0 0 0
1 1 1 0 1 1 0 0 1 0
0
1
0 0
1 0
1
0 0
0
0 1
0
0 1
10
0
010
0 1 1 0 1
11
1-
6-( )
13+( )
1+
78-( )
1- 2-
´
Multiplication requiring only n/2 summands.