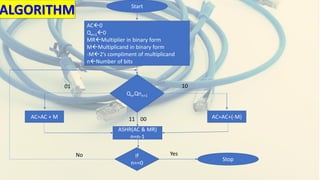
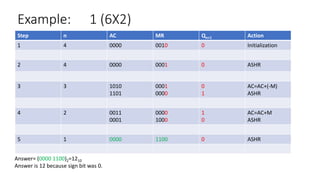
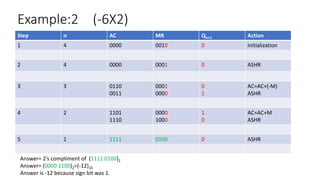
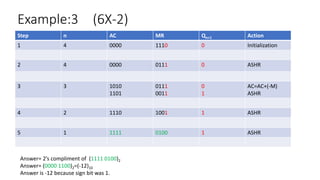
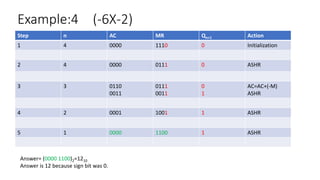
Booth's algorithm provides an efficient method for multiplying signed binary integers using 2's complement representation, reducing the number of required additions and subtractions. The document details several examples, demonstrating the steps involved in multiplying different pairs of signed integers using specific initial values and actions throughout the process. Additionally, it explains key components such as the accumulator, sequence counter, and arithmetic shift right operations.

1. BOOTH’S ALGORITHM FOR
SIGNED MULTIPLICATION
• Booth algorithm gives a procedure for
multiplying binary integers in signed 2’s
complement representation in efficient way,
i.e., less number of additions/subtractions
required.

2. Start
AC0
Qn+10
MRMultiplier in binary form
MMultiplicand in binary form
-M2’s compliment of multiplicand
nNumber of bits
Qn,Qnn+1
AC=AC + M AC=AC+(-M)
ASHR(AC & MR)
n=n-1
If
n==0
Stop
ALGORITHM
YesNo
01 10
11 00

3. HARDWARE IMPLEMENTATION
M AC MR Qn+1
Qn
ALU
ADD/SUB

4. Example:1
(6X2)
• Multiplicand=(6)10
• We will convert Multiplicand into binary form we will name it M.
M=(0110)2
• We will find 2’s compliment of M and we will name it –M.
-M=(1010)2
• Multiplier=(2)10
• We will find binary form of Multiplier.
MR=(0010)2
• AC=Accumulator
• SC=Sequence Counter is set to a number n equal to the number of
bits in the multiplier.
• Qn+1=An extra flip-flop appended to QR to facilitate a double
inspection of the multiplier.
• ASHR= Arithmetic Shift Right.

5. Example: 1 (6X2)
Step n AC MR Qn+1 Action
1 4 0000 0010 0 Initialization
2 4 0000 0001 0 ASHR
3 3 1010
1101
0001
0000
0
1
AC=AC+(-M)
ASHR
4 2 0011
0001
0000
1000
1
0
AC=AC+M
ASHR
5 1 0000 1100 0 ASHR
Answer= (0000 1100)2=1210
Answer is 12 because sign bit was 0.

6. Example:2
(-6X2)
• Multiplicand=(-6)10
• We will convert Multiplicand into binary form we will name it M.
M=(1010)2
• We will find 2’s compliment of M and we will name it –M.
-M=(0110)2
• Multiplier=(2)10
• We will find binary form of Multiplier.
MR=(0010)2
• AC=Accumulator
• SC=Sequence Counter is set to a number n equal to the number of
bits in the multiplier.
• Qn+1=An extra flip-flop appended to QR to facilitate a double
inspection of the multiplier.
• ASHR= Arithmetic Shift Right.

7. Example:2 (-6X2)
Step n AC MR Qn+1 Action
1 4 0000 0010 0 Initialization
2 4 0000 0001 0 ASHR
3 3 0110
0011
0001
0000
0
1
AC=AC+(-M)
ASHR
4 2 1101
1110
0000
1000
1
0
AC=AC+M
ASHR
5 1 1111 0100 0 ASHR
Answer= 2’s compliment of (1111 0100)2
Answer= (0000 1100)2=(-12)10
Answer is -12 because sign bit was 1.

8. Example:3
(6X-2)
• Multiplicand=(6)10
• We will convert Multiplicand into binary form we will name it M.
M=(0110)2
• We will find 2’s compliment of M and we will name it –M.
-M=(1010)2
• Multiplier=(-2)10
• We will find binary form of Multiplier.
MR=(1110)2
• AC=Accumulator
• SC=Sequence Counter is set to a number n equal to the number of
bits in the multiplier.
• Qn+1=An extra flip-flop appended to QR to facilitate a double
inspection of the multiplier.
• ARS= ASHR= Arithmetic Shift Right.

9. Example:3 (6X-2)
Step n AC MR Qn+1 Action
1 4 0000 1110 0 Initialization
2 4 0000 0111 0 ASHR
3 3 1010
1101
0111
0011
0
1
AC=AC+(-M)
ASHR
4 2 1110 1001 1 ASHR
5 1 1111 0100 1 ASHR
Answer= 2’s compliment of (1111 0100)2
Answer= (0000 1100)2=(-12)10
Answer is -12 because sign bit was 1.

10. Example:4
(-6X-2)
• Multiplicand=(-6)10
• We will convert Multiplicand into binary form we will name it M.
M=(1010)2
• We will find 2’s compliment of M and we will name it –M.
-M=(0110)2
• Multiplier=(-2)10
• We will find binary form of Multiplier.
MR=(1110)2
• AC=Accumulator
• SC=Sequence Counter is set to a number n equal to the number of
bits in the multiplier.
• Qn+1=An extra flip-flop appended to QR to facilitate a double
inspection of the multiplier.
• ASHR= Arithmetic Shift Right.

11. Example:4 (-6X-2)
Step n AC MR Qn+1 Action
1 4 0000 1110 0 Initialization
2 4 0000 0111 0 ASHR
3 3 0110
0011
0111
0011
0
1
AC=AC+(-M)
ASHR
4 2 0001 1001 1 ASHR
5 1 0000 1100 1 ASHR
Answer= (0000 1100)2=1210
Answer is 12 because sign bit was 0.