Downloaded 136 times
![BCD SUBTRACTION
DECIMA
L
DIGIT
9’s
COMPLE
MENT
0 9
4 5
The step as flowing :
(a) ADD 9’s COMP. OF B TO A
(b) IF RESULT > 9, CORRECT BY
ADDING 0110
(c) IF MOST SIGNIFICANT CARRY
IS PRODUCED [i.e. =1] THEN
THE RESULT IS POSITIVE AND
THE END ARROUND CARRY MUST
BE ADDED.
(d) IF MOST SIGNIFICANT CARRY
IS 0 [i.e. NO CARRY] THEN THE
RESULT IS NEGATIVE AND WE
GET THE 9’s COMP. OF THE RESULT.](https://image.slidesharecdn.com/presentation1-150625133139-lva1-app6892/85/Arithmetic-Logic-Unit-14-320.jpg)
Uploaded byDeyaa Ahmed
Arithmetic Logic Unit .
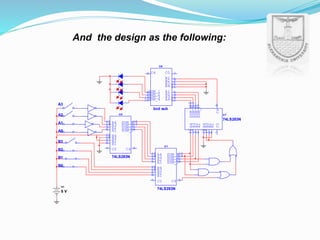
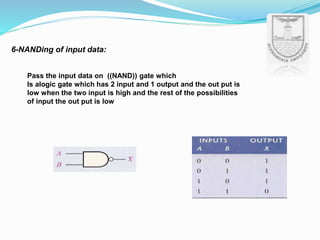
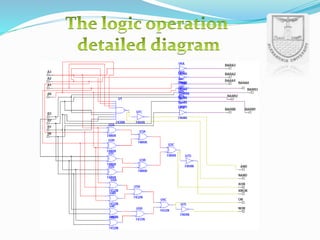
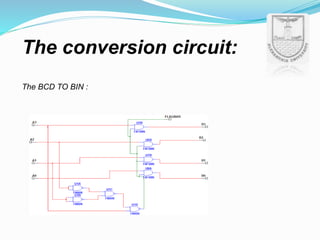
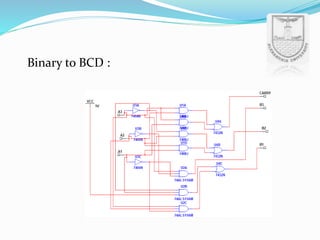
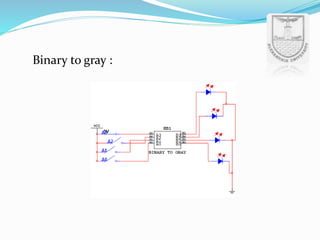
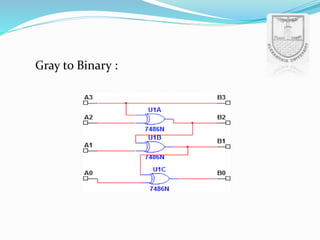
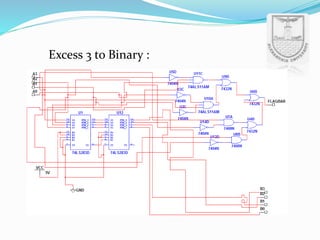
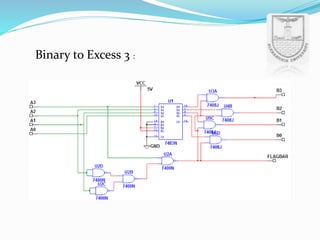
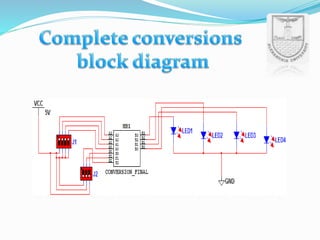
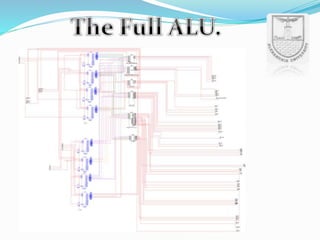
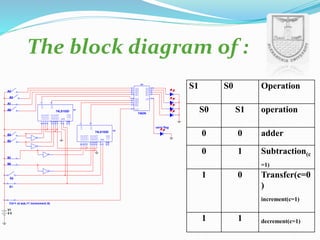
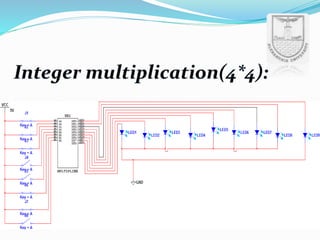
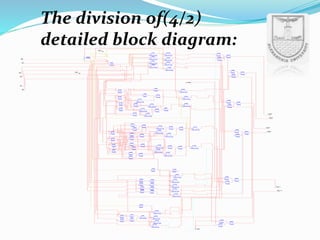
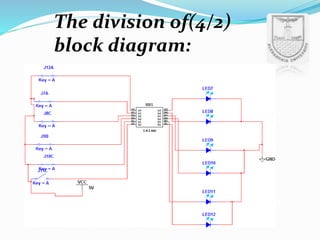
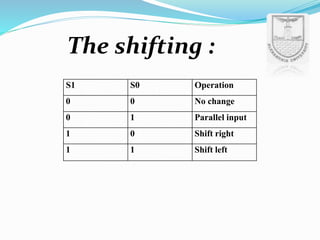
An arithmetic logic unit (ALU) is a digital circuit essential for performing arithmetic and logical operations within a computer's CPU. The concept proposed by John von Neumann in 1945 remains crucial in computer science, with ongoing research focused on enhancing ALU capabilities in modern CPUs and GPUs. The document further details various operations, block diagrams, and the functionality of ALUs, including BCD addition and different logic operations.
More Related Content
Similar to Arithmetic Logic Unit .
Arithmetic Logic Unit .
- 4. In computing, anarithmetic logic unit (ALU) is a digital circuit that performs arithmetic and logical operations. The ALU is a fundamental building block of the central processing unit (CPU) of a computer, and even the simplest microprocessors contain one for purposes such as maintaining timers. The processors found inside modern CPUs and graphics processing units (GPUs) accommodate very powerful and very complex ALUs; a single component may contain a number of ALUs. Mathematician John von Neumann proposed the ALU concept in 1945, when he wrote a report on the foundations for a new computer called the EDVAC. Research into ALUs remains an important part of computer science, falling under Arithmetic and logic structures in the ACM Computing Classification System.
- 6. Addition with carryof two 4-bit data :
- 7. The block diagramof : U2 7483N A28 B27 A110 C013 B111 S4 15 S3 2 C4 14 A41 B416 A33 B34 S2 6 S1 9 V1 5 V A3 A2 A1 A0 B3 B2 B1 B0 S0 U1 74LS153D 2Y92C010 2C111 2C212 2C313 A14 B2 ~1G1 1Y71C06 1C15 1C24 1C33 ~2G15 S1 U4 74LS153D 2Y92C010 2C111 2C212 2C313 A14 B2 ~1G1 1Y71C06 1C15 1C24 1C33 ~2G15 Ci(=1 at sub,=1 increament A) carry flag S1 S0 Operation S0 S1 operation 0 0 adder 0 1 Subtraction(c =1) 1 0 Transfer(c=0 ) increment(c=1) 1 1 decrement(c=1)
- 9. The division of(4/2) detailedblock diagram:U1A 74ALS11AM U1B 74ALS11AM U2B 74ALS11AM U56C 74ALS11AM U6B 7404N GND VCC 5V U12A 7404N U13B 7404N U15B 7404N U16B 7404N U8A 7408J U8B 7408J U9B 7432N U11B 7432N U17A 74ALS11AM U18A 74ALS11AM U19A 74ALS11AM U21B 7432N U24B 7432N U25B 7432N U27A 74ALS11AM U22B 74ALS21AM U7B 7408J U32B 7408J U10B 7432N U14B 7432N U20B 7432N U36D 7408J U37D 7408J U39B 7432N U23A 74ALS11AM U28B 74ALS11AM U29D 74ALS21AM U33D 7408J U26D 7408J U34B 7432N U35B 7432N U38B 7432N U40D 7408J U41D 7408J U42B 7432N U43A 74ALS11AM U44B 74ALS11AM U45A 7404N U46B 7404N U47B 7404N U48B 7404N U49D 7408J U50D 7408J U51D 7408J U52C 7408J U53A 7404N U53B 7404N U54B 7404N U55B 7404N U3A 7408J U4A 7408J U5A 74ALS32M U31A 7404N U31B 7404N U61A 74ALS11AM U62A 74ALS11AM U63A 74ALS11AM U64A 74ALS11AM U65B 7404N U66A 74ALS11AM U67A 74ALS11AM U68A 74ALS11AM U70A 74ALS11AM U71A 74ALS11AM U72A 74ALS11AM U73A 74ALS11AM U74A 74ALS11AM U75A 74ALS11AM U77A 74ALS11AM U78A 7404N U79A 7404N U80A 74ALS11AM U81A 74ALS11AM U82A 74ALS11AM U83A 74ALS11AM U84B 7404N VCC 5V U10A 7432N U30B 7432N U57A 7432N U58A 7432N U59B 7432N U60A 7432N U69A 7432N U76B 7432N U85A 7432N U86A 7432N U87B 7432N U88A 7432N U89A 7432N U90B 7432N U91A 7432N U92A 7432N U93B 7432N U94A 7432N GND OUT0 OUT1 OUT2 OUT3 R0_1_4 R_1_2 A2 A3 S1 S0 A0 A1
- 10. The division of(4/2) blockdiagram:
- 11. U8 74LS283N SUM_4 10 SUM_3 13 SUM_14 SUM_2 1 C4 9 B411 A412 B315 A314 B22 A23 B16 A15 C07 V3 5 V A3 A2 A1 A0 1's com 2's com
- 12. The shifting : S1S0 Operation 0 0 No change 0 1 Parallel input 1 0 Shift right 1 1 Shift left
- 13. V1 5 V A3 A2 A1 A0 B3 B2 B1 B0 Ci U2 74LS283N SUM_4 10 SUM_313 SUM_1 4 SUM_2 1 C4 9 B411 A412 B315 A314 B22 A23 B16 A15 C07 U1 74LS283N SUM_410 SUM_313 SUM_14 SUM_21 C49 B411 A412 B315 A314 B22 A23 B16 A15 C07 BCD adder sum>9 carry flag The BCD addition of the input data:
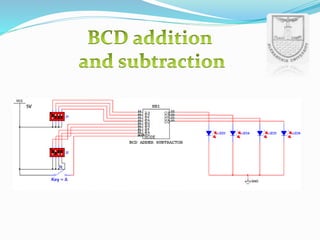
- 14. BCD SUBTRACTION DECIMA L DIGIT 9’s COMPLE MENT 0 9 45 The step as flowing : (a) ADD 9’s COMP. OF B TO A (b) IF RESULT > 9, CORRECT BY ADDING 0110 (c) IF MOST SIGNIFICANT CARRY IS PRODUCED [i.e. =1] THEN THE RESULT IS POSITIVE AND THE END ARROUND CARRY MUST BE ADDED. (d) IF MOST SIGNIFICANT CARRY IS 0 [i.e. NO CARRY] THEN THE RESULT IS NEGATIVE AND WE GET THE 9’s COMP. OF THE RESULT.
- 15. And the designas the following: U1 74LS283N SUM_410 SUM_313 SUM_14SUM_21 C4 9 B411 A412 B315 A314 B22 A23 B16 A15 C07 U2 74LS283N SUM_410 SUM_313 SUM_14SUM_21 C4 9 B411 A412 B315 A314 B22 A23 B16 A15 C07 U7 74LS283N SUM_410 SUM_313 SUM_14SUM_21 C49 B411 A412 B315 A314 B22 A23 B16 A15 C07 U8 bcd sub SUM_410 SUM_313 SUM_14SUM_21 C49 B4 11 A4 12 B3 15 A3 14 B2 2 A2 3 B1 6 A1 5 C0 7 V1 5 V A3 A2 A1 A0 B3 B2 B1 B0
- 17. Logic operation: 1-Anding theinput data:
- 18. 2-ORing of inputdata:
- 19. 3- XORing ofinput data :
- 20. 4- XNORing ofinput data:
- 21. 5-inverting of input data: Pass the input data on ((NOT)) gate which Is alogic gate that has one input and one output , the output is low when the input is high and the output is high when input is low
- 22. 6-NANDing of inputdata: Pass the input data on ((NAND)) gate which Is alogic gate which has 2 input and 1 output and the out put is low when the two input is high and the rest of the possibilities of input the out put is low
- 23. 7-NORing of inputdata: Pass the input data on ((NOR)) gate which is a logic gate that Has 2input and 1 out put and the out put is high only when the two input is low , the rest of the possibilities of input the out put is low.
- 25. Comparing of twoinput data for equality operation:
- 26. Comparing of twoinput data for larger than and smaller than operation :
- 27. The conversion circuit: TheBCD TO BIN :
- 28.
- 29.
- 30.
- 31. Excess 3 toBinary :
- 32.