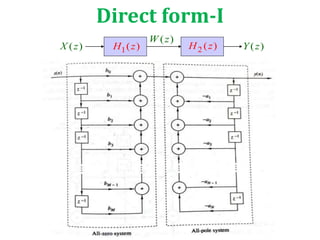
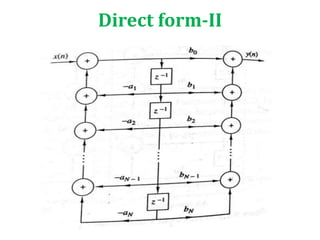
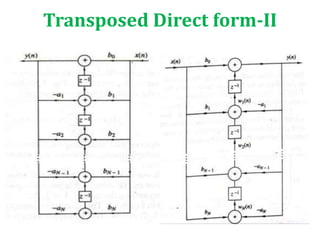
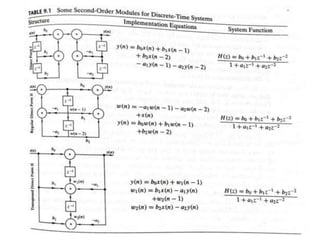
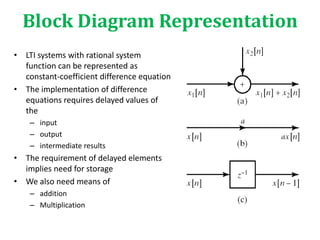
This document compares and contrasts FIR and IIR filters. It then discusses different implementation structures for digital filters, including block diagrams, FIR filter reviews, and basic IIR filter structures like direct form I and II and transposed direct form II. Basic IIR filters are characterized by rational transfer functions that can be represented using difference equations, requiring feedback and storage of delayed input, output, and intermediate values.

1. Implementation of Basic
Digital Filter Structures

5. FIR - IIR filters comparison
• FIR
– Simpler to design
– Inherently stable
– Can be designed to have linear phase
– Require lower bit precision
• IIR
– Need less taps (memory, multiplications)
– Can simulate analog filters

6. Block Diagram Representation
• LTI systems with rational system
function can be represented as
constant-coefficient difference equation
• The implementation of difference
equations requires delayed values of
the
– input
– output
– intermediate results
• The requirement of delayed elements
implies need for storage
• We also need means of
– addition
– Multiplication

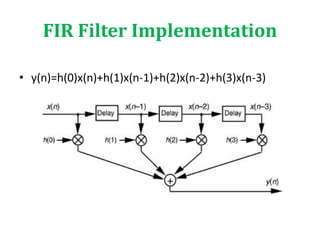
7. FIR Filter Review
Z-1
Z-1
Z-1
+
h0
h1
h2
h3
x[n]
x[n-1]
y[n]
x[n-2]
x[n-3]



3
0
)(
n
n
n zhzH

8. FIR Filter Implementation
• y(n)=h(0)x(n)+h(1)x(n-1)+h(2)x(n-2)+h(3)x(n-3)

9. Basic IIR Digital Filter Structures
• The causal IIR digital filters we are concerned
with in this course are characterized by a real
rational transfer function of or, equivalently
by a constant coefficient difference equation
• From the difference equation representation, it
can be seen that the realization of the causal
IIR digital filters requires some form of
feedback
1
z

10. Basic IIR Digital Filter Structures
• An N-th order IIR digital transfer function is
characterized by 2N+1 unique coefficients,
and in general, requires 2N+1 multipliers
and 2N two-input adders for
implementation
• Direct form IIR filters: Filter structures in
which the multiplier coefficients are
precisely the coefficients of the transfer
function

11. Direct form-I
)(zH1 )(zH2
)(zW
)(zX )(zY

12. Direct form-II

13. Transposed Direct form-II

14. Second-Order Modules
for Discrete Time
Systems