This document contains formulas and equations related to finite element analysis (FEA) for one-dimensional structural and heat transfer problems. It includes formulas for weighted residual methods, Ritz method, beam deflection and stress, springs, one-dimensional bars and frames, and one-dimensional heat transfer through walls and fins. Displacement functions, stiffness matrices, thermal loads, and conduction/convection equations are provided for linear and quadratic elements undergoing static structural and thermal analysis.






![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 7
N1 Shape Function at node 1
u1 Displacement at node 1
N2 Shape Function at node 2
u2 Displacement at node 2
N3 Shape Function at node 3
u3 Displacement at node 2
Stiffness Matrix:
For 1D linear bar element
[ 𝑘] =
𝐴𝐸
𝑙
[
1 −1
−1 1
]
For 1D quadratic element
[ 𝑘] =
𝐴𝐸
3𝑙
[
7 1 −8
1 7 −8
−8 −8 16
]
A Area of the element - mm2
E Young’s Modulus of the element - N/mm2
l Length of the element - mm
General Force Equation:
{ 𝐹} = [ 𝑘] { 𝑢}
{𝐹} Force vector (Global)
[𝑘] Global stiffness matrix
{𝑢} Displacement matrix
Reaction Force:
{ 𝑅} = [ 𝑘] { 𝑢} − { 𝐹}
{𝑅} Reaction force
If The Body Is Subjected To Self – Weight:
For 1D linear bar element
{ 𝐹} =
𝜌𝐴𝑙
2
{
1
1
}](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-7-320.jpg)
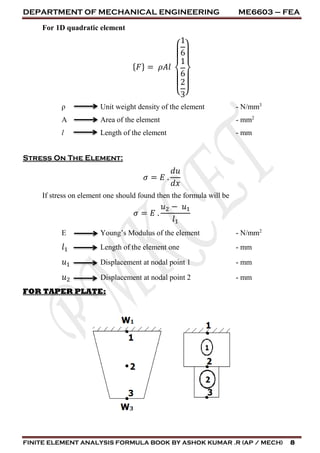
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 9
For rectangular cross section
Area = Width * Thickness
At any point of x
𝐴 𝑥 = 𝐴1 − (𝐴1 − 𝐴3)
𝑥
𝑙
Area at node 1:
𝐴1 = 𝑊1 ∗ 𝑡1
Area at node 2(Applicable only for mid – point):
𝐴2 = 𝑊2 ∗ 𝑡2
𝐴2 = (
𝑊1 + 𝑊3
2
) ∗ 𝑡2
Area at node 3:
𝐴3 = 𝑊3 ∗ 𝑡3
Average area of element 1:
𝐴
=
𝐴1+ 𝐴2
2
Average area of element 2:
𝐴
=
𝐴2 + 𝐴3
2
For circular cross section
𝐴𝑟𝑒𝑎 =
𝜋
4
𝑑2
TEMPERATURE EFFECTS ON STRUCTURAL PROBLEM:
Stiffness Matrix:
[ 𝑘] =
𝐴𝐸
𝑙
[
1 −1
−1 1
]
A Area of the element - mm2
E Young’s Modulus of the element - N/mm2
l Length of the element - mm](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-9-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 10
Thermal Load:
{ 𝐹} = 𝐸𝐴𝛼∆𝑇 {
−1
1
}
A Area of the element - mm2
E Young’s Modulus of the element - N/mm2
α Coefficient of thermal expansion - /˚C
∆T Temperature difference
Thermal Stress:
{ 𝜎} = 𝐸
𝑑𝑢
𝑑𝑥
− 𝐸𝛼∆𝑇
𝐸𝛼∆𝑇 Thermal Strain
For element 1
{ 𝜎} = 𝐸1
𝑢2 − 𝑢1
𝑙1
− 𝐸1 𝛼1∆𝑇
Reaction Force:
{ 𝑅} = [ 𝑘] { 𝑢} − { 𝐹}
{𝑅} Reaction force
{𝐹} Force vector (Global)
[𝑘] Global stiffness matrix
{𝑢} Displacement matrix
SPRINGS:
Stiffness Matrix:
[ 𝑘] = 𝑘 [
1 −1
−1 1
]
k Stiffness of the spring - N/mm
HEAT TRANSFER:
ONE DIMENSIONAL HEAT TRANSFER ON WALL:
Global Stiffness Matrix When Wall Subjected To Conduction:
[ 𝐾] { 𝑇} = { 𝐹}
{𝐹} Force vector (Global)](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-10-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 11
[𝐾] Global stiffness matrix
{𝑇} Temperature matrix
[ 𝐾] =
𝐴𝑘
𝑙
[
1 −1
−1 1
]
𝐴𝑘
𝑙
[
1 −1
−1 1
] {
𝑇1
𝑇2
} = {
𝐹1
𝐹2
}
A Area of the wall - m2
k Thermal conductivity of wall - W/mK
l Length of the wall - m
Global Stiffness Matrix When Wall Subjected To Conduction &
Convection:
[ 𝐾𝑐] =
𝐴𝑘
𝑙
[
1 −1
−1 1
]
[ 𝐾ℎ] = ℎ𝐴 [
0 0
0 1
]
[ 𝐾] = [ 𝐾𝑐] + [ 𝐾ℎ]
[ 𝐾] { 𝑇} = { 𝐹}
[
𝐴𝑘
𝑙
[
1 −1
−1 1
] + ℎ𝐴 [
0 0
0 1
]] {
𝑇1
𝑇2
} = ℎ𝑇∞ 𝐴 {
0
1
}
A Area of the wall - m2
k Thermal conductivity of wall - W/mK
l Length of the wall - m
h Heat transfer coefficient - W/m2
K
𝑇∞ Atmospheric air temperature - K](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-11-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 12
ONE DIMENSIONAL HEAT TRANSFER ON FIN:
Global Stiffness Matrix When Fin Subjected To Conduction &
Convection:
[ 𝐾𝑐] =
𝐴𝑘
𝑙
[
1 −1
−1 1
]
[ 𝐾ℎ] =
ℎ𝑃𝑙
6
[
2 1
1 2
]
[ 𝐾] = [ 𝐾𝑐] + [ 𝐾ℎ]
[ 𝐾] { 𝑇} = { 𝐹}
[
𝐴𝑘
𝑙
[
1 −1
−1 1
] +
ℎ𝑃𝑙
6
[
2 1
1 2
]] {
𝑇1
𝑇2
} =
𝑄𝐴𝑙 + 𝑃ℎ𝑇∞ 𝑙
2
{
1
1
}
𝐴 = 𝐿𝑒𝑛𝑔𝑡ℎ ∗ 𝑇ℎ𝑖𝑐𝑘𝑒𝑛𝑠𝑠 = 𝑙 ∗ 𝑡
𝑃 = 2 ∗ 𝑙 (𝐴𝑝𝑝𝑟𝑜𝑥𝑖𝑚𝑎𝑡𝑒𝑙𝑦)
A Area of the fin - m2
P Perimeter of the fin - m
k Thermal conductivity of fin - W/mK
l Length of the fin - m
h Heat transfer coefficient - W/m2
K
𝑇∞ Atmospheric air temperature - K
Q Heat Generation - W](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-12-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 13
TRUSSES:
Stiffness Matrix:
[ 𝑘] =
𝐸𝑒 𝐴 𝑒
𝑙 𝑒
[
𝑙2
𝑙𝑚 −𝑙2
−𝑙𝑚
𝑙𝑚 𝑚2
−𝑙𝑚 −𝑚2
−𝑙2
−𝑙𝑚 𝑙2
𝑙𝑚
−𝑙𝑚 −𝑚2
𝑙𝑚 𝑚2
]
Ae Area of the element - mm2
Ee Young’s Modulus of the element - N/mm2
le Length of the element - mm
Length of element 1
𝑙 = √( 𝑥2 − 𝑥1)2 + ( 𝑦2 − 𝑦1)2
𝑙 =
𝑥2 − 𝑥1
𝑙
𝑚 =
𝑦2 − 𝑦1
𝑙
Stress:
Stress of element 1
𝜎 =
𝐸
𝑙
[−𝑙1 −𝑚1 𝑙1 𝑚1] {
𝑢1
𝑢2
𝑢3
𝑢4
}
u matrix varies according the element](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-13-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 14
BEAMS:
Displacement Function:
𝑢 = 𝑁1 𝑢1 + 𝑁2 𝑢2 + 𝑁3 𝑢3 + 𝑁4 𝑢4
𝑁1 =
1
𝐿3
(2𝑥3
− 3𝑥2
𝐿 + 𝐿3)
𝑁2 =
1
𝐿3
( 𝑥3
𝐿 − 2𝑥2
𝐿2
+ 𝑥𝐿3)
𝑁3 =
1
𝐿3
(− 2𝑥3
+ 3𝑥2
𝐿)
𝑁4 =
1
𝐿3
( 𝑥3
𝐿 − 𝑥2
𝐿2)
N1 Shape Function at node 1
u1 Displacement at node 1
N2 Shape Function at node 2
u2 Displacement at node 2
N3 Shape Function at node 3
u3 Displacement at node 3
N4 Shape Function at node 4
u4 Displacement at node 4
Stiffness Matrix:
[ 𝑘] =
𝐸𝐼
𝐿3
[
12 6𝐿 −12 6𝐿
6𝐿 4𝐿2
−6𝐿 2𝐿2
−12 −6𝐿 12 −6𝐿
6𝐿 2𝐿2
−6𝐿 4𝐿2
]
I Moment of Inertia - mm4
E Young’s Modulus - N/mm2
L Length of the beam - mm](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-14-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 16
S.No
LOADING
CASE
F1 m1 F2 m2
5)
−7𝑤𝐿
20
−𝑤𝐿2
20
−3𝑤𝐿
20
𝑤𝐿2
30
6)
−𝑤𝐿
4
−5𝑤𝐿2
96
−𝑤𝐿
4
5𝑤𝐿2
96
7)
−13𝑤𝐿
32
−11𝑤𝐿2
192
−3𝑤𝐿
32
5𝑤𝐿2
192
LONGITUDINAL VIBRATION OF BAR:
General Finite Element Equation:
{[ 𝐾] − [ 𝑚] 𝜔2} { 𝑢} = { 𝐹}
[𝐾] Stiffness matrix
[𝑚] Mass matrix
{𝐹} External Force](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-16-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 17
{𝑢} Displacement matrix
𝜔 Natural Frequency - rad / sec
Stiffness Matrix:
[ 𝐾] =
𝐴𝐸
𝑙
[
1 −1
−1 1
]
A Area of the element - mm2
E Young’s Modulus of the element - N/mm2
l Length of the element - mm
Lumped Mass Matrix:
NOTE: Unless mention in the problem to use lumped mass matrix we should not
use this. If nothing is mentioned use consistent mass matrix only
[ 𝑚] =
𝜌𝐴𝑙
2
[
1 0
0 1
]
ρ Unit weight density of the element - N/mm3
A Area of the element - mm2
l Length of the element - mm
Consistent Mass Matrix:
NOTE: If nothing is mentioned use consistent mass matrix only
[ 𝑚] =
𝜌𝐴𝑙
6
[
2 1
1 2
]
ρ Unit weight density of the element - N/mm3
A Area of the element - mm2
l Length of the element - mm
TRANSVERSE VIBRATION OF BEAMS:
General Finite Element Equation:
{[ 𝐾] − [ 𝑚] 𝜔2} { 𝑢} = { 𝐹}
[𝐾] Stiffness matrix
[𝑚] Mass matrix
{𝐹} External Force
{𝑢} Displacement matrix
𝜔 Natural Frequency - rad / sec](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-17-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 18
Stiffness Matrix:
[ 𝑘] =
𝐸𝐼
𝐿3
[
12 6𝐿 −12 6𝐿
6𝐿 4𝐿2
−6𝐿 2𝐿2
−12 −6𝐿 12 −6𝐿
6𝐿 2𝐿2
−6𝐿 4𝐿2
]
I Moment of Inertia - mm4
E Young’s Modulus - N/mm2
L Length of the beam - mm
Lumped Mass Matrix:
NOTE: Unless mention in the problem to use lumped mass matrix we should not
use this. If nothing is mentioned use consistent mass matrix only
[ 𝑚] =
𝜌𝐴𝑙
2
[
1 0 0 0
0 0 0 0
0 0 1 0
0 0 0 0
]
ρ Unit weight density of the element - N/mm3
A Area of the element - mm2
l Length of the element - mm
Consistent Mass Matrix:
NOTE: If nothing is mentioned use consistent mass matrix only
[ 𝑚] =
𝜌𝐴𝑙
420
[
156 22𝑙 54 −13𝑙
22𝑙 4𝑙2
13𝑙 −3𝑙2
54 13𝑙 156 −22𝑙
−13𝑙 −3𝑙2
−22𝑙 4𝑙2
]
ρ Unit weight density of the element - N/mm3
A Area of the element - mm2
l Length of the element - mm
EIGEN VALUES & EIGEN VECTORS:
General Finite Element Equation:
{[ 𝐾] − [ 𝑚] 𝜆} { 𝑢} = 0
[𝐾] Stiffness matrix
[𝑚] Mass matrix](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-18-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 19
{𝑢} Displacement matrix
𝜆 Eigen values
Determinant Method:
|[ 𝐾] − [ 𝑚] 𝜆| = 0
[𝐾] Stiffness matrix
[𝑚] Mass matrix
𝜆 Eigen values
Natural Frequency of Bar Element:
𝜆 = 𝜔2
𝑓 =
1
2𝜋
𝜔
𝑓 Frequency of bar - Hz
[𝑚] Mass matrix
𝜆 Eigen values
𝜔 Natural Frequency - rad / sec](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-19-320.jpg)



![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 23
TWO DIMENSIONAL HEAT TRANSFER:
Stiffness Matrix When Subjected To Conduction:
[ 𝐾𝑐] = [ 𝐵] 𝑇 [ 𝐷] [ 𝐵] 𝐴 𝑡
[𝐵] Strain Displacement matrix
[𝐷] Material Property matrix
t Thickness of the triangular element - mm
𝐴 Area of the triangular element - mm2
Strain Displacement Matrix:
[ 𝐵] =
1
2𝐴
[
𝑞1 𝑞2 𝑞3
𝑟1 𝑟2 𝑟3
]
𝑞1 = 𝑦2 − 𝑦3
𝑞2 = 𝑦3 − 𝑦1
𝑞3 = 𝑦1 − 𝑦2
𝑟1 = 𝑥3 − 𝑥2
𝑟2 = 𝑥1 − 𝑥3
𝑟3 = 𝑥2 − 𝑥1
Area:
𝐴 =
1
2
|
1 𝑥1 𝑦1
1 𝑥2 𝑦2
1 𝑥3 𝑦3
|
Material Property Matrix:
[ 𝐷] = [
𝑘 𝑥𝑥 0
0 𝑘 𝑦𝑦
]
kxx & kyy Thermal conductivity - W/mK](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-23-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 24
Stiffness Matrix When Subjected To Conduction:
[𝐾𝑐] =
𝑘
4𝐴
[
𝑏1
2
+ 𝑐1
2
𝑏1 𝑏2 + 𝑐1 𝑐2 𝑏1 𝑏3 + 𝑐1 𝑐3
𝑏1 𝑏2 + 𝑐1 𝑐2 𝑏2
2
+ 𝑐2
2
𝑏2 𝑏3 + 𝑐2 𝑐3
𝑏1 𝑏3 + 𝑐1 𝑐3 𝑏2 𝑏3 + 𝑐2 𝑐3 𝑏3
2
+ 𝑐3
2
]
𝑏1 = 𝑦2 − 𝑦3
𝑏2 = 𝑦3 − 𝑦1
𝑏3 = 𝑦1 − 𝑦2
𝑐1 = 𝑥3 − 𝑥2
𝑐2 = 𝑥1 − 𝑥3
𝑐3 = 𝑥2 − 𝑥1
k Thermal conductivity - W/mK
𝐴 Area of the triangular element - mm2
Stiffness Matrix When Subjected To Convection:
If side 1-2 is subjected to convection
[ 𝐾ℎ] =
ℎ1−2 𝑙1−2 𝑡
6
[
2 1 0
1 2 0
0 0 0
]
If side 2-3 is subjected to convection
[ 𝐾ℎ] =
ℎ2−3 𝑙2−3 𝑡
6
[
0 0 0
0 2 1
0 1 2
]
If side 1-3 is subjected to convection
𝐾ℎ =
ℎ1−3 𝑙1−3 𝑡
6
[
2 0 1
0 0 0
1 0 2
]
Stiffness Matrix When Subjected To Conduction & Convection:
If side 1-2 is subjected to convection
[ 𝐾] = [ 𝐾𝑐] + [ 𝐾ℎ]](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-24-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 25
[ 𝐾] = [ 𝐵] 𝑇 [ 𝐷] [ 𝐵] 𝐴 𝑡 +
ℎ1−2 𝑙1−2 𝑡
6
[
2 1 0
1 2 0
0 0 0
]
If side 2-3 is subjected to convection
[ 𝐾] = [ 𝐾𝑐] + [ 𝐾ℎ]
[ 𝐾] = [ 𝐵] 𝑇 [ 𝐷] [ 𝐵] 𝐴 𝑡 +
ℎ2−3 𝑙2−3 𝑡
6
[
0 0 0
0 2 1
0 1 2
]
If side 1-3 is subjected to convection
[ 𝐾] = [ 𝐾𝑐] + [ 𝐾ℎ]
[ 𝐾] = [ 𝐵] 𝑇 [ 𝐷] [ 𝐵] 𝐴 𝑡 +
ℎ1−3 𝑙1−3 𝑡
6
[
2 0 1
0 0 0
1 0 2
]
Where
𝑙1−2 = √(𝑥2 − 𝑥1)2 + (𝑦2 − 𝑦1)2
𝑙2−3 = √(𝑥3 − 𝑥2)2 + (𝑦3 − 𝑦2)2
𝑙1−3 = √(𝑥3 − 𝑥1)2 + (𝑦3 − 𝑦1)2
[𝐵] Strain Displacement matrix
[𝐷] Material Property matrix
t Thickness of the triangular element - mm
𝐴 Area of the triangular element - mm2
l Length of the side subjected to convection - m
h Heat transfer coefficient - W/m2
K
Force Vector For Convection:
If side 1-2 is subjected to convection
𝐹 =
ℎ1−2 𝑇∞ 𝑙1−2 𝑡
2
[
1
1
0
]
If side 2-3 is subjected to convection
𝐹 =
ℎ2−3 𝑇∞ 𝑙2−3 𝑡
2
[
0
1
1
]
If side 1-3 is subjected to convection](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-25-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 26
𝐹 =
ℎ1−3 𝑇∞ 𝑙1−3 𝑡
2
[
1
0
1
]
𝑇∞ Atmospheric air temperature - K
t Thickness of the triangular element - mm
l Length of the side subjected to convection - m
h Heat transfer coefficient - W/m2
K
Force Vector If Heat Source Is Given:
𝐹 =
𝑄𝑉
3
[
1
1
1
]
𝑉 = 𝐴 ∗ 𝑡
Q Heat Source - W/m3
V Volume of triangular element - m3
A Area of triangular element - m2
t Thickness of the triangular element - mm
Force Vector If Heat Flux Is Given:
If side 1-2 is subjected to heat flux
𝐹 =
𝑞𝑙1−2 𝑡
2
[
1
1
0
]
If side 2- 3 is subjected to heat flux
𝐹 =
𝑞𝑙2−3 𝑡
2
[
0
1
1
]
If side 1-3 is subjected to heat flux
𝐹 =
𝑞𝑙1−3 𝑡
2
[
1
0
1
]](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-26-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 27
TORSION:
Shape Function:
𝑁1 =
𝑝1 + 𝑞1 𝑥 + 𝑟1 𝑦
2𝐴
𝑁2 =
𝑝2 + 𝑞2 𝑥 + 𝑟2 𝑦
2𝐴
𝑁3 =
𝑝3 + 𝑞3 𝑥 + 𝑟3 𝑦
2𝐴
𝑝1 = 𝑥2 𝑦3 − 𝑥3 𝑦2
𝑝2 = 𝑥3 𝑦1 − 𝑥1 𝑦3
𝑝3 = 𝑥1 𝑦2 − 𝑥2 𝑦1
𝑞1 = 𝑦2 − 𝑦3
𝑞2 = 𝑦3 − 𝑦1
𝑞3 = 𝑦1 − 𝑦2
𝑟1 = 𝑥3 − 𝑥2
𝑟2 = 𝑥1 − 𝑥3
𝑟3 = 𝑥2 − 𝑥1
Shape Function Equation:
𝜑(𝑥, 𝑦) = 𝜑1 𝑁1 + 𝜑2 𝑁2 + 𝜑3 𝑁3
Strain Displacement Matrix:
[ 𝐵] =
1
2𝐴
[
𝑞1 𝑞2 𝑞3
𝑟1 𝑟2 𝑟3
]
𝑞1 = 𝑦2 − 𝑦3
𝑞2 = 𝑦3 − 𝑦1
𝑞3 = 𝑦1 − 𝑦2
𝑟1 = 𝑥3 − 𝑥2](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-27-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 28
𝑟2 = 𝑥1 − 𝑥3
𝑟3 = 𝑥2 − 𝑥1
Area:
𝐴 =
1
2
|
1 𝑥1 𝑦1
1 𝑥2 𝑦2
1 𝑥3 𝑦3
|
Stiffness Matrix When Subjected To Torsion:
[ 𝐾] = [ 𝐵] 𝑇[ 𝐵] 𝐴
[𝐵] Strain Displacement matrix
𝐴 Area of the triangular element - mm2
We know that
[ 𝐾] [ 𝜑] = [ 𝐹]
[𝐾] Stiffness matrix
[𝜑] Shear Function
[𝐹] Force Vector
Force Vector in Torsion:
𝐹𝑇 =
2𝐺𝜃𝐴
3
[
1
1
1
]
𝜃 Angle of Twist - ◦
G Modulus of Rigidity - N / mm2
𝐴 Area of the triangular element - mm2
Total Torque:
𝑇 =
2𝐴
3
( 𝜑1 + 𝜑2 + 𝜑3)
𝜑 Shear Function
𝐴 Area of the triangular element - mm2
For an example if an element is taken as shown in Fig](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-28-320.jpg)


![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 31
When all the shape function is given
𝑥 = 𝑁1 𝑥1 + 𝑁2 𝑥2 + 𝑁3 𝑥3
𝑦 = 𝑁1 𝑦1 + 𝑁2 𝑦2 + 𝑁3 𝑦3
When two or one shape function is given
𝑥 = ( 𝑥1 − 𝑥3) 𝑁1 + ( 𝑥2 − 𝑥3) 𝑁2 + 𝑥3
𝑦 = ( 𝑦1 − 𝑦3) 𝑁1 + ( 𝑦2 − 𝑦3) 𝑁2 + 𝑦3
Strain Displacement Matrix:
[ 𝐵] =
1
2𝐴
[
𝑞1 0 𝑞2 0 𝑞3 0
0 𝑟1 0 𝑟2 0 𝑟3
𝑟1 𝑞1 𝑟2 𝑞2 𝑟3 𝑞3
]
A Area of the triangular element - mm2
𝑞1 = 𝑦2 − 𝑦3
𝑞2 = 𝑦3 − 𝑦1
𝑞3 = 𝑦1 − 𝑦2
𝑟1 = 𝑥3 − 𝑥2
𝑟2 = 𝑥1 − 𝑥3
𝑟3 = 𝑥2 − 𝑥1
Stress Strain Relationship Matrix:
For Plane Stress condition:
[ 𝐷] =
𝐸
1 − 𝛾2
[
1 𝛾 0
𝛾 1 0
0 0
1 − 𝛾
2
]
For Plane Strain condition:
[ 𝐷] =
𝐸
(1 + 𝛾)(1 − 2𝛾)
[
(1 − 𝛾) 𝛾 0
𝛾 (1 − 𝛾) 0
0 0
(1 − 2𝛾)
2
]
E Young’s Modulus - N/mm2
γ Poisson’s ratio](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-31-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 32
Stiffness Matrix:
[ 𝐾] = [ 𝐵] 𝑇 [ 𝐷] [ 𝐵] 𝐴 𝑡
[𝐵] Strain Displacement matrix
[𝐷] Stress – Strain Relationship matrix
t Thickness of the triangular element - mm
𝐴 Area of the triangular element - mm2
Force Vector:
When self – weight is considered or density of material is given
𝐹 =
𝜌𝐴𝑡
3
[
1
1
1
]
𝜌 Density - Kg/m3
𝐴 Area - m2
𝑡 Thickness - m
To Convert Traction Force Into Nodal Force:
𝐹 =
1
2
𝑇 𝐴
𝐹 =
1
2
𝑇 (𝑏 ∗ 𝑡)
𝐹 Nodal force - N
𝑇 Surface traction - N / mm2
t Thickness of the element - mm](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-32-320.jpg)


![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 35
t Thickness of the element - mm
L Length of the element - mm
Element Stress:
{ 𝜎} = [ 𝐷] [ 𝐵] { 𝑢}
{
𝜎𝑥
𝜎 𝑦
𝜏 𝑥𝑦
} = [ 𝐷] [ 𝐵]
{
𝑢1
𝑣1
𝑢2
𝑣2
𝑢3
𝑣3}
𝜎𝑥 Normal stress in x direction - N/mm2
𝜎 𝑦 Normal stress in y direction - N/mm2
𝜏 𝑥𝑦 Shear Stress - N/mm2
u & v Nodal displacement - mm
Maximum Normal Stress:
𝜎 𝑚𝑎𝑥 = 𝜎1 =
𝜎𝑥 + 𝜎 𝑦
2
+ √(
𝜎𝑥 − 𝜎 𝑦
2
)
2
+ 𝜏2
𝑥𝑦
Minimum Normal Stress:
𝜎 𝑚𝑎𝑥 = 𝜎1 =
𝜎𝑥 + 𝜎 𝑦
2
− √(
𝜎𝑥 − 𝜎 𝑦
2
)
2
+ 𝜏2
𝑥𝑦
Principle Angle:
tan 2𝜃 𝑝 =
2𝜏 𝑥𝑦
𝜎𝑥 − 𝜎 𝑦
Element Strain:
{ 𝑒} = [ 𝐵] { 𝑢}](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-35-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 36
{
𝑒 𝑥
𝑒 𝑦
𝛾𝑥𝑦
} = [ 𝐵]
{
𝑢1
𝑣1
𝑢2
𝑣2
𝑢3
𝑣3}
𝜎𝑥 Normal strain in x direction - N/mm2
𝜎 𝑦 Normal strain in y direction - N/mm2
𝜏 𝑥𝑦 Shear Stress - N/mm2
u & v Nodal displacement - mm
TEMPERATURE EFFECTS:
Initial Strain:
For Plane Stress condition:
{ 𝑒0} = {
𝛼∆𝑇
𝛼∆𝑇
0
}
For Plane Strain condition:
{ 𝑒0} = (1 + 𝛾) {
𝛼∆𝑇
𝛼∆𝑇
0
}
α Coefficient of thermal expansion - /˚C
∆T Temperature difference ˚C
γ Poisson’s ratio
Element Temperature Force:
{𝐹} = [ 𝐵] 𝑇 [ 𝐷] { 𝑒0} 𝐴 𝑡
[𝐵] Strain Displacement matrix
[𝐷] Stress – Strain Relationship matrix
{𝑒0} Initial strain
t Thickness of the triangular element - mm
𝐴 Area of the triangular element - mm2](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-36-320.jpg)

![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 38
Strain Displacement Matrix:
[ 𝐵] =
1
2𝐴
[
𝛽1 0 𝛽2 0 𝛽3 0
𝛼1
𝑟
+ 𝛽1 +
𝛾1 𝑧
𝑟
0
𝛼2
𝑟
+ 𝛽2 +
𝛾2 𝑧
𝑟
0
𝛼3
𝑟
+ 𝛽3 +
𝛾3 𝑧
𝑟
0
0 𝛾1 0 𝛾2 0 𝛾3
𝛾1 𝛽1 𝛾2 𝛽2 𝛾3 𝛽3]
A Area of the triangular element - mm2
𝛼1 = 𝑟2 𝑧3 − 𝑟3 𝑧2
𝛼2 = 𝑟3 𝑧1 − 𝑟1 𝑧3
𝛼3 = 𝑟1 𝑧2 − 𝑟2 𝑧1
𝛽1 = 𝑧2 − 𝑧3
𝛽2 = 𝑧3 − 𝑧1
𝛽3 = 𝑧1 − 𝑧2
𝛾1 = 𝑟3 − 𝑟2
𝛾2 = 𝑟1 − 𝑟3
𝛾3 = 𝑟2 − 𝑟1
Stress Strain Relationship Matrix:
[ 𝐷] =
𝐸
(1 + 𝛾)(1 − 2𝛾)
[
1 − 𝛾 𝛾 𝛾 0
𝛾 1 − 𝛾 𝛾 0
𝛾 𝛾 1 − 𝛾 0
0 0 0
1 − 2𝛾
2 ]
E Young’s Modulus - N/mm2
γ Poisson’s ratio
Stiffness Matrix:
[ 𝐾] = 2𝜋𝑟𝐴 [ 𝐵] 𝑇 [ 𝐷] [ 𝐵]
𝑟 =
𝑟1 + 𝑟2 + 𝑟3
3](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-38-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 39
[𝐵] Strain Displacement matrix
[𝐷] Stress – Strain Relationship matrix
r Radius of the triangular element - mm
𝐴 Area of the triangular element - mm2
Element Stress:
{ 𝜎} = [ 𝐷] [ 𝐵] { 𝑢}
{
𝜎𝑟
𝜎 𝜃
𝜎𝑧
𝜏 𝑟𝑧
} = [ 𝐷] [ 𝐵]
{
𝑢1
𝑤1
𝑢2
𝑤2
𝑢3
𝑤3}
𝜎𝑟 Radial stress - N/mm2
𝜎 𝜃 Circumferential stress - N/mm2
𝜎𝑧 Longitudinal stress - N/mm2
𝜏 𝑟𝑧 Shear Stress - N/mm2
u & w Nodal displacement - mm
TEMPERATURE EFFECTS:
Thermal Force Vector:
[ 𝐹] 𝑡 = 2𝜋𝑟𝐴 [ 𝐵] 𝑇 [ 𝐷] { 𝑒0}
𝑟 =
𝑟1 + 𝑟2 + 𝑟3
3
[𝐵] Strain Displacement matrix
[𝐷] Stress – Strain Relationship matrix
{ 𝑒0} Strain matrix
r Radius of the triangular element - mm
𝐴 Area of the triangular element - mm2
Strain:](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-39-320.jpg)

![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 41
ISOPARAMETRIC ELEMENT:
FOUR NODED QUADRILATERAL:
Shape Function:
𝑁1 =
1
4
(1 − 𝜀) (1 − 𝜂)
𝑁2 =
1
4
(1 + 𝜀) (1 − 𝜂)
𝑁3 =
1
4
(1 + 𝜀) (1 + 𝜂)
𝑁4 =
1
4
(1 − 𝜀) (1 + 𝜂)
𝑥 = 𝑁1 𝑥1 + 𝑁2 𝑥2 + 𝑁3 𝑥3 + 𝑁4 𝑥4
𝑦 = 𝑁1 𝑦1 + 𝑁2 𝑦2 + 𝑁3 𝑦3 + 𝑁4 𝑦4
Jacobian Matrix:
[ 𝐽] =
[
𝜕𝑥
𝜕𝜀
𝜕𝑦
𝜕𝜀
𝜕𝑥
𝜕𝜂
𝜕𝑦
𝜕𝜂]
[ 𝐽] = [
𝐽11 𝐽12
𝐽21 𝐽22
]
UNIT V – ISOPARAMETRIC FORMULATION](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-41-320.jpg)
![DEPARTMENT OF MECHANICAL ENGINEERING ME6603 – FEA
FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 42
𝐽11 =
1
4
[− (1 − 𝜂) 𝑥1 + (1 − 𝜂) 𝑥2 + (1 + 𝜂) 𝑥3 − (1 + 𝜂) 𝑥4 ]
𝐽12 =
1
4
[− (1 − 𝜂) 𝑦1 + (1 − 𝜂) 𝑦2 + (1 + 𝜂) 𝑦3 − (1 + 𝜂) 𝑦4 ]
𝐽21 =
1
4
[− (1 − 𝜀) 𝑥1 − (1 + 𝜀) 𝑥2 + (1 + 𝜀) 𝑥3 + (1 − 𝜀) 𝑥4 ]
𝐽21 =
1
4
[− (1 − 𝜀) 𝑦1 − (1 + 𝜀) 𝑦2 + (1 + 𝜀) 𝑦3 + (1 − 𝜀) 𝑦4 ]
Strain Displacement Matrix:
[ 𝐵] =
1
| 𝐽|
[
𝐽22 −𝐽12 0 0
0 0 −𝐽21 𝐽11
−𝐽21 𝐽11 𝐽22 −𝐽12
] ∗
1
4
[
−(1 − 𝜂) 0 (1 − 𝜂) 0 (1 + 𝜂) 0 −(1 + 𝜂) 0
−(1 − 𝜀) 0 −(1 + 𝜀) 0 (1 + 𝜀) 0 (1 − 𝜀) 0
0 −(1 − 𝜂) 0 (1 − 𝜂) 0 (1 + 𝜂) 0 −(1 + 𝜂)
0 −(1 − 𝜀) 0 −(1 + 𝜀) 0 (1 + 𝜀) 0 (1 − 𝜀) ]](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-42-320.jpg)
![FINITE ELEMENT ANALYSIS FORMULA BOOK BY ASHOK KUMAR .R (AP / MECH) 43
Stress Strain Relationship Matrix:
For Plane Stress condition:
[ 𝐷] =
𝐸
1 − 𝛾2
[
1 𝛾 0
𝛾 1 0
0 0
1 − 𝛾
2
]
For Plane Stress condition:
[ 𝐷] =
1
(1 + 𝛾)(1 − 2𝛾)
[
(1 − 𝛾) 𝛾 0
𝛾 (1 − 𝛾) 0
0 0
(1 − 2𝛾)
2
]
E Young’s Modulus - N/mm2
γ Poisson’s ratio
Stiffness Matrix:
For Isoparametric Quadrilateral Element:
[ 𝐾] = 𝑡 ∬[ 𝐵] 𝑇 [ 𝐷] [ 𝐵] 𝜕𝑥 𝜕𝑦
For Natural Co – Ordinates
[𝐾] = 𝑡 ∫ ∫ [ 𝐵] 𝑇 [ 𝐷] [ 𝐵] ∗ | 𝐽| ∗ 𝜕𝜀 ∗ 𝜕𝜂
1
−1
1
−1
[𝐵] Strain Displacement matrix
[𝐷] Stress – Strain Relationship matrix
|𝐽| Determinant of the Jacobian matrix
ε,η Natural Co – Ordinates
t Thickness of the element - mm
𝐴 Area of the triangular element - mm2
SIX NODED QUADRILATERAL:
Shape Function:
𝑁1 = 2 (𝐿1 −
1
2
) 𝐿1](https://image.slidesharecdn.com/feaformulabook2013reg-171225162541/85/ME6603-FINITE-ELEMENT-ANALYSIS-FORMULA-BOOK-43-320.jpg)


