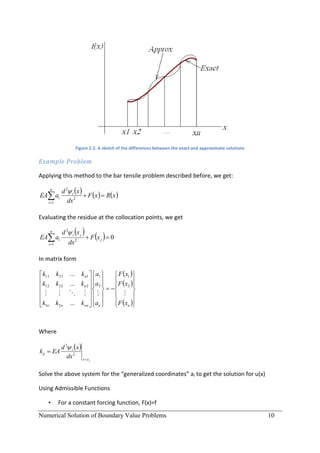
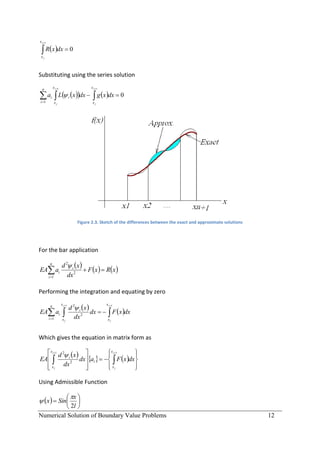
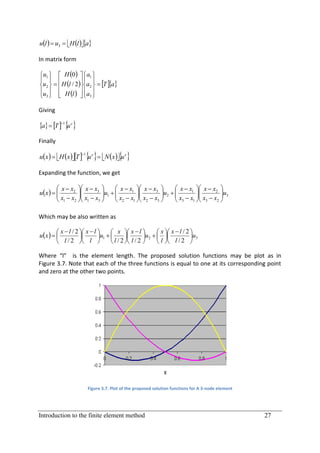
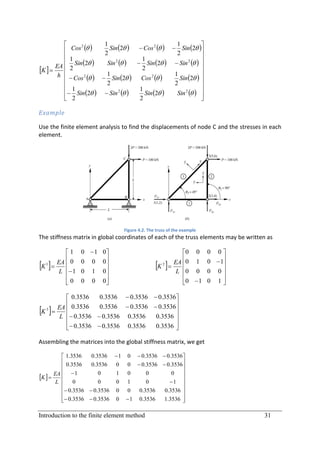
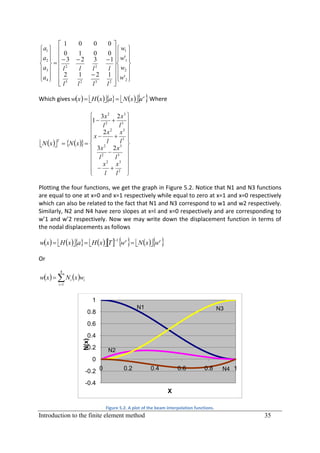
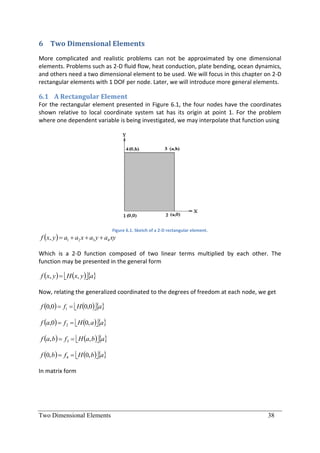
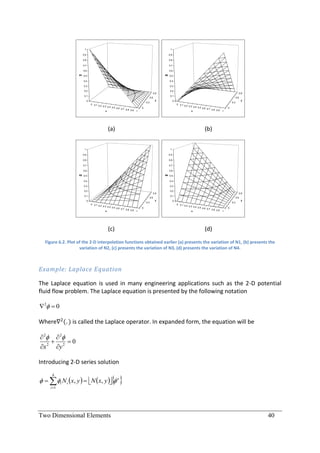
This document provides an introduction to finite element analysis. It discusses numerical solutions to boundary value problems using weighted residual methods, including the general weighted residual method, collocation method, subdomain method, and Galerkin method. It then introduces the finite element method, covering discretization, element equations, assembling elements, applying boundary conditions, and solving. It also discusses finite element modeling of trusses, beams, frames, plates, and coupled fields. The overall aim is to develop the necessary tools for modeling physical problems using finite element analysis.






























![The symbolic manipulator MATHEMATICA may be used to derive the trial functions N(x) as
presented below
In[2]:= Hw 1, x, x x, x x x ;
Hwx D Hw, x ;
Hwxx D Hwx, x ;
In[5]:= x 0; Tb1 Hw; Tb2 Hwx;
x L; Tb3 Hw; Tb4 Hwx;
Clear x ;
TB Tb1, Tb2, Tb3, Tb4
TBINV Inverse TB
Out[8]= 1, 0, 0, 0 , 0, 1, 0, 0 , 1, L, L 2 , L 3 , 0, 1, 2 L, 3 L 2
3 2 3 1 2 1 2 1
Out[9]= 1, 0, 0, 0 , 0, 1, 0, 0 , , , , , , , ,
2 2 3 2 3
L L L L L L L L2
In[10]:= NN Hw.TBINV
3 x2 2 x3 2 x2 x3 3 x2 2 x3 x2 x3
Out[10]= 1 , x , ,
2 3 2 2 3
L L L L L L L L2
In[11]:= Simplify NN
L x 2 L 2x L x 2x 3L 2 x x2 x2 L x
Out[11]= , , ,
3 2 3
L L L L2
5.3 Beam Stiffness Matrix
Recall that the governing equation is
d2 d 2w
EI x 2 F ( x)
dx 2
dx
Substituting with the series solution obtained in the previous section
4
wx N i x wi
i 1
The governing equation becomes
4
d2 d 2N
dx 2 EI x 2 i wi F ( x) R( x)
i 1 dx
Applying Galerkin method:
Beams and Frames 36](https://image.slidesharecdn.com/chapterx1introductiontothefiniteemementmethod-100714092729-phpapp02/85/Introduction-to-the-Finite-Element-Method-36-320.jpg)
![le le
4 d2 d 2N
R( x) N j dx 2 EI x 2 i wi F ( x) N j dx
dx
0 0 i 1 dx
Using integration by parts, twice, we get:
le
4 2
d 2N j
EI x d N i wi F ( x) N j dx 0
i1 dx 2 dx 2
0
In matrix form
le le
EI x N N dxw F ( x)N xx dx
e
xx xx
0 0
Using MATHEMATICA, we get
In[2]:= Hw 1, x, x x, x x x ;
Hwx D Hw, x ;
Hwxx D Hwx, x ;
In[5]:= x 0; Tb1 Hw; Tb2 Hwx;
x L; Tb3 Hw; Tb4 Hwx;
Clear x ;
TB Tb1, Tb2, Tb3, Tb4
TBINV Inverse TB
Out[8]= 1, 0, 0, 0 , 0, 1, 0, 0 , 1, L, L 2 , L 3 , 0, 1, 2 L, 3 L 2
3 2 3 1 2 1 2 1
Out[9]= 1, 0, 0, 0 , 0, 1, 0, 0 , , , , , , , ,
2 2 3 2 3
L L L L L L L L2
In[10]:= NN Hw.TBINV
3 x2 2 x3 2 x2 x3 3 x2 2 x3 x2 x3
Out[10]= 1 , x , ,
L2 L3 L L2 L2 L3 L L2
In[11]:= Simplify NN
L x 2 L 2x L x 2x 3L 2 x x2 x2 L x
Out[11]= , , ,
3 2 3 2
L L L L
Giving the stiffness matrix to be
Introduction to the finite element method 37](https://image.slidesharecdn.com/chapterx1introductiontothefiniteemementmethod-100714092729-phpapp02/85/Introduction-to-the-Finite-Element-Method-37-320.jpg)















![7.4 Finite Element Model of Plates in Bending
7.4.1 Displacement Function
The transverse displacement w(x,y), at any location x and y inside the plate element, is
expressed by
w( x, y) H w a ( -1)
7
where H w is a 64 element row vector and {a} is the vector of unknown coefficients. For
the plate element under consideration, the bending degrees of freedom associated with
each node are
w
w H a
x w 1
w H w,x a2
( -2)
7
y H w, y
2 w H w,x , y a16
xy
where Hw,i is the partial derivative of Hw with respect to i. Substituting the nodal coordinates
into equation (13), the nodal bending displacement vector {wb} is obtained as follows,
wb Tb a ( -3)
7
w1
w1
H w 0,0
x H 0,0
w1 w,x
H w, y 0,0
where wb y [Tb ] ( -4)
7
H w,x , y 0,0
2 &
w1
xy
2 w4 H w,x , y 0, b
xy
From equation (14), we can obtain
a Tb 1wb ( -5)
7
Substituting equation (16) into equation (12) gives
Introduction to the finite element method 55](https://image.slidesharecdn.com/chapterx1introductiontothefiniteemementmethod-100714092729-phpapp02/85/Introduction-to-the-Finite-Element-Method-55-320.jpg)
![w( x, y) H w Tb wb N w wb
1
( -6)
7
where [Nw] is the shape function for bending given by
N w H w Tb 1 ( -7)
7
7.4.2 Strain-Displacement Relation
Consider the classical plate theory, for the strain vector {} can be written in terms of the
lateral deflections as follows
x
y z
( -8)
7
xy
where z is the vertical distance from the neutral plane and {} is the curvature vector which
can be written as,
2w
2
2 x
w
2 Cb { a } ( -9)
7
y2
w
2 xy
where
Hw
, xx
Cb H w, yy ( -10)
7
2 H
w, xy
Substituting equation (17) into equation (23), gives
Cb Tb 1{wb } Bb { wb } ( -11)
7
where
Bb Cb Tb 1 ( -12)
7
Thus, the strain-nodal displacement relationship can be written as
Stationary Functional Approach 56](https://image.slidesharecdn.com/chapterx1introductiontothefiniteemementmethod-100714092729-phpapp02/85/Introduction-to-the-Finite-Element-Method-56-320.jpg)


![The terms of the expansion of equation (35) can be recast as follows
z B w Q B w dV w k w ,
2 T D T
b b b b b b b
V
z B w e N wD dV wb T kbD wD ,
T
b b D
V
N
V
D wD T eT z Bb wb dV wD T k Db wb wD T kbD T wb ,
and N
V
D wD T N D wD dV wD T k D wD ;
where [kb] is bending stiffness matrix, [kbD] is bending displacement-electric displacement
coupling matrix, and [kD] is the electric stiffness matrix.
7.4.4.2 The Kinetic Energy
The variation of the kinetic energy T of the plate/piezo patch element is given by,
2w
A
T w h 2 dA
t
( -22)
7
where is the density/equivalent density and h is the thickness of the element. The above
equation can be rewritten in terms of nodal displacements as follows
2w
dA h wb T N w T N w wb dA wb T mb wb
A
w h
2
t A
( -23)
7
where [mb] is the element bending mass matrix.
7.4.4.3 The external work
The variation of the external work done exerted by the shunt circuit is given by
W DLqdA
( -24)
7
A
Introduction to the finite element method 59](https://image.slidesharecdn.com/chapterx1introductiontothefiniteemementmethod-100714092729-phpapp02/85/Introduction-to-the-Finite-Element-Method-59-320.jpg)
![where A is the element area, L is the shunted inductance, and q is the charge flowing in the
circuit. But, as the charge is the integral of the electric displacement over the element area;
then equation (38) reduces to,
W DdA LDdA
( -25)
7
A A
Substituting from equation (20), gives
W wD T N D T dA N D LwD dA
( -26)
7
A A
which can be recast in the following form,
W wD T mD wD
( -27)
7
where [mD] is the element electric mass matrix.
Finally, the element equation of motion with no external forces can be written as
mb 0 wb k b
k bD wb 0
0 w k
mD D Db
k D wD 0
( -28)
7
Stationary Functional Approach 60](https://image.slidesharecdn.com/chapterx1introductiontothefiniteemementmethod-100714092729-phpapp02/85/Introduction-to-the-Finite-Element-Method-60-320.jpg)