Mechanical Engineering Assignment Help

Mechanical Engineering Assignment Help
Finite Element Analysis
For any Assignment related queries, Call us at : - +1 (315) 557-6473
You can mail us at : - info@mechanicalengineeringassignmenthelp.com
Reach us at : - https://www.mechanicalengineeringassignmenthelp.com/

https://www.solidworksassignmenthelp.com/
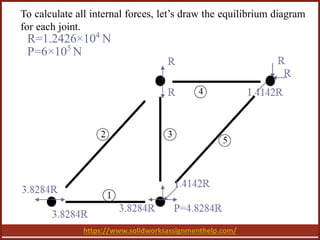
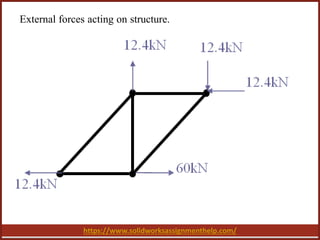
Finite Element Analysis (FEA) is a powerful computational tool
used in engineering to analyze and predict the behavior of
structures and fluids under various conditions. In the context of
"Finite Element Analysis of Solids and Fluids I," this presentation
delves into a fundamental problem involving the analysis of a
truss structure. The truss problem is a classic example used to
illustrate the application of FEA in linear elastic analysis. By
removing displacement boundary conditions and applying no
external loads, the problem offers an opportunity to explore the
inherent properties and responses of the structure. This analysis
not only provides insights into the displacement and internal
forces of the truss but also demonstrates the equilibrium
conditions essential for structural integrity.
Introduction

Problem 1
Consider the truss problem already discussed in class, in linear elastic analysis, but with
all displacement boundary conditions removed and no applied load.
A⎡m ⎤ = cross-sectional area of each bar, E
Y
X

a) Develop by the physical reasoning used in class that is “by inspection” the K
matrix for
b) Now assume U1 U2  U4 U7  U8  0 and the external loads, R3  0 , R5 
60kN , and R6  0 . Calculate the displacements, U3 , U5 , and U6 and sketch the
deflected shape of the structure.

c) Calculate all internal element forces and the reactions
corresponding to U1 , U2 , U4 , U7 and U8 .
d) Show explicitly that element 3 and joint (node) 3 are in
equilibrium. Show that the complete structure is in equilibrium.

Solution 2
The truss geometry is shown below. Bar mumbers are circled. Joint numbers
are placed adjacent to their respective joints.
For a linear static
analysis, we have:
K8×8U8×1=R8×1

a) The K matrix is calculated column by column. The ith
column of the stiffness matrix represents the external force
vector required to give the structure unit displacement about
the ith
degree of freedom and zero displacement about all other
degree of freedom. Take a look at one example how to construct
it.
Calculate column 5:
Imposing the following displacement pattern:
U5=1, U1=U2=U3=U4=U6=U7=U8=0

The resulting external force vector under this set of displacement
conditions is equal to the 5th
column of the stiffness matrix K. In
this case, the truss bar 1 changes length by 1, the truss bar 5
shrinks by , ,and all other truss bars are fixed in length.
Hence, the bar axial forces are as follows.

Positive and negative signs of the axial forces imply
tension and compression, respectively. Hence the
reaction forces, the entries of the 5th
column, are
obtained from the equilibrium equations at the joints.

After assembling all columns, the following K is determined:

b) Since U1  U2 U4 U7  U8  0 , we can reduce K8×8U8×1=R8×1 to
KaaUa=Ra as follows:

The solution is

c) Since we know the values of U3 , U5 , and U6 , we can calculate the
reaction forces from KbaUa=Rb,

The undeformed and deformed meshes with applied boundary
conditions and loads are plotted on the next page.

To calculate all internal forces, let’s draw the equilibrium diagram
for each joint.
R=1.2426×104
N
P=6×105
N

Therefore, the internal forces are
Element 1: tension 4.7572×104
N Element 2: no force
Element 3: tension 1.2426×104
N
Element 4: no force
Element 5: Compression 1.7573×104
N

and Reactions:

d) We can make sure that element 3 and joint 3 are in equilibrium
explicitly by the diagram below.

External forces acting on structure.

∑ F x  12.4kN  47.6kN  60kN  0
∑ F y  12.4kN 12.4kN  0
∑ Mat 4  12.4kN  a  47.6kN  a  60kN  a
 0
Therefore, the structure is in equilibrium.

Conclusion
In conclusion, the truss problem presented in this session highlights
the essential principles of Finite Element Analysis as applied to
structural mechanics. By meticulously developing the stiffness matrix,
imposing boundary conditions, and calculating displacements and
internal forces, we gain a comprehensive understanding of the
behavior of truss structures. This problem underscores the
importance of equilibrium in ensuring the stability of structures. The
methods and results discussed here are foundational to the broader
applications of FEA in both solids and fluids, emphasizing its critical
role in modern engineering analysis and design. Through such
detailed studies, we pave the way for more complex and accurate
simulations, ultimately leading to safer and more efficient
engineering solutions.

Thank You

Mechanical Engineering Assignment Help

More Related Content

Similar to Mechanical Engineering Assignment Help

More from Mechanical Engineering Assignment Help

Recently uploaded

Mechanical Engineering Assignment Help