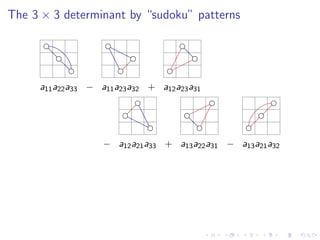
This document provides information about determinants of matrices including: 1) It defines the determinant of a 2x2 matrix as a11a22 - a12a21 and provides patterns for calculating the determinant of a 3x3 matrix. 2) It explains that the determinant of an nxn matrix is the sum of all products of n elements with one from each row and column, with a positive or negative sign depending on the number of upward lines. 3) It describes how to calculate the determinant of a 3x3 matrix using cofactors, which are minors multiplied by positive or negative one. The determinant is then expressed as a sum of entries multiplied by their cofactors.

1. Lesson 6
Determinants (Section 13.3–5)
Math 20
October 3, 2007
Announcements
Thomas Schelling at IOP (79 JFK Street), Wednesday 6pm
Problem Set 3 is on the course web site. Due October 10
Sign up for conference times on course website
My office hours: Mondays 1–2, Tuesdays 3–4, Wednesdays
1–3 (SC 323)

2. The determinant
Definition
a11 a12
The determinant of a 2 × 2 matrix A = is the number
a21 a22
a11 a12
= a11 a22 − a21 a12
a21 a22

4. The determinant
Definition
The determinant of a 3 × 3 matrix is
a11 a12 a13
a21 a22 a23 = a11 a22 a33 − a11 a23 a32 − a21 a12 a33
a31 a32 a33
+ a21 a13 a32 + a31 a12 a23 − a31 a22 a13

5. The 3 × 3 determinant by “sudoku” patterns
a11 a22 a33 − a11 a23 a32 + a12 a23 a31
− a12 a21 a33 + a13 a22 a31 − a13 a21 a32

7. The 3 × 3 determinant by “sudoku” patterns
a11 a22 a33 − a11 a23 a32 + a12 a23 a31
− a12 a21 a33 + a13 a22 a31 − a13 a21 a32
Observations
These are all the ways we can put three dots, one in each row
and column
The sign is positive if the number of “up” lines is even,
negative if it’s odd

9. The 3 × 3 determinant by cofactors
We can compute a 3 × 3 determinant in terms of smaller
determinants:
a11 a12 a13
a21 a22 a23 = a11 a22 a33 − a11 a23 a32 + a12 a31 a23
a31 a32 a33
− a12 a21 a33 + a13 a21 a32 − a13 a31 a22
a22 a23 a a a a
− a12 21 23 + a13 21 22
= a11
a32 a33 a31 a33 a31 a32

11. Example
Example
12 3
Compute 2 −3 2
3 1 −1

12. Example
Example
12 3
Compute 2 −3 2
3 1 −1
Solution
50.

13. Determinants of n × n matrices by patterns
Definition
Let A = (aij )n×n be a matrix. The determinant of A is a sum of
all products of n elements of the matrix, where each product takes
exactly one entry from each row and column.

14. Determinants of n × n matrices by patterns
Definition
Let A = (aij )n×n be a matrix. The determinant of A is a sum of
all products of n elements of the matrix, where each product takes
exactly one entry from each row and column.
The sign of each product is given by (−1)σ , where σ is the number
of upwards lines used when all the entries in a pattern are
connected.

15. 4 × 4 sudoku patterns
− − −
+ + +
− − −
+ + +
− − −
+ + +
− − −
+ + +

16. Determinants of n × n matrices by cofactors
Definition
Let A = (aij )n×n be a matrix. The (i, j)-minor of A is the matrix
obtained from A by deleting the ith row and j column. This matrix
has dimensions (n − 1) × (n − 1).
The (i, j) cofactor of A is the determinant of the (i, j) minor
times (−1)i+j .

17. The 3 × 3 determinant by cofactors
We can compute a 3 × 3 determinant in terms of smaller
determinants:
a11 a12 a13
a21 a22 a23 = a11 a22 a33 − a11 a23 a32 + a12 a31 a23
a31 a32 a33
− a12 a21 a33 + a13 a21 a32 − a13 a31 a22
a22 a23 a a a a
− a12 21 23 + a13 21 22
= a11
a32 a33 a31 a33 a31 a32

18. The 3 × 3 determinant by cofactors
We can compute a 3 × 3 determinant in terms of smaller
determinants:
a11 a12 a13
a21 a22 a23 = a11 a22 a33 − a11 a23 a32 + a12 a31 a23
a31 a32 a33
− a12 a21 a33 + a13 a21 a32 − a13 a31 a22
a22 a23 a a a a
− a12 21 23 + a13 21 22
= a11
a32 a33 a31 a33 a31 a32
= a11 C11 + a12 C12 + a13 C13

19. Fact
The determinant of A = (aij )n×n is the sum
a11 C11 + a12 C12 + · · · + a1n C1n