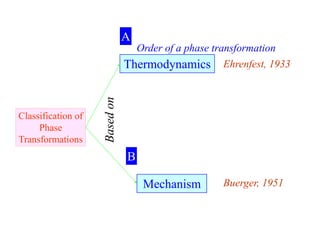
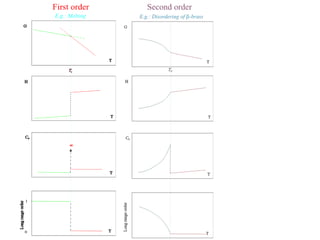
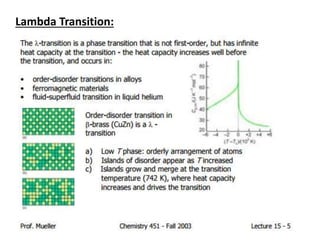
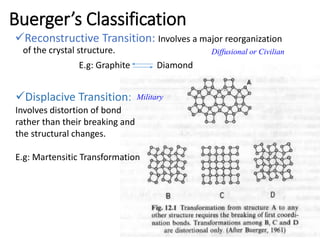
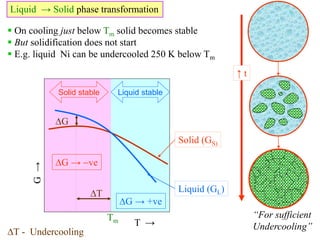
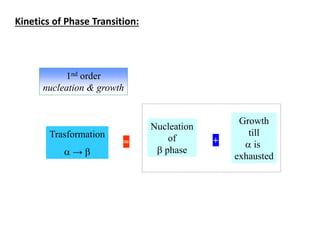
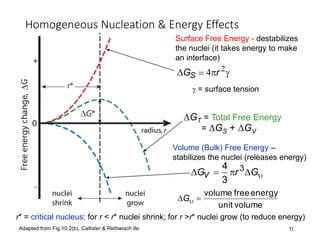
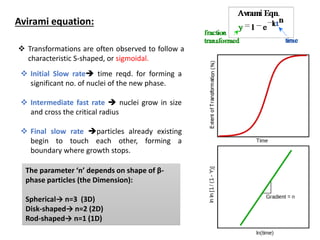
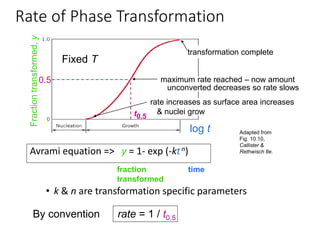
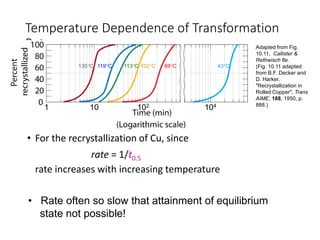
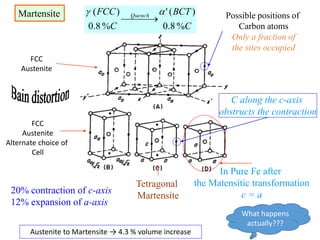
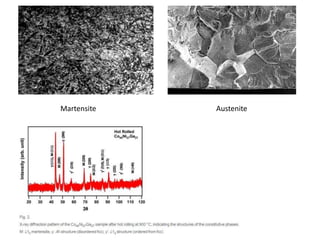
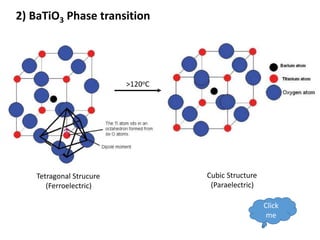
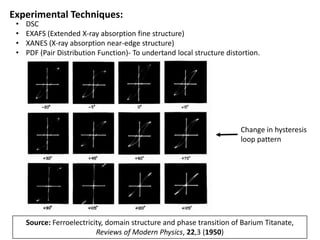
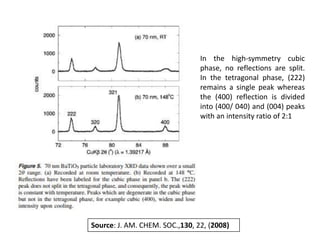
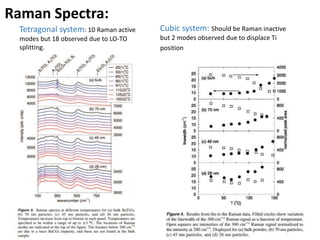
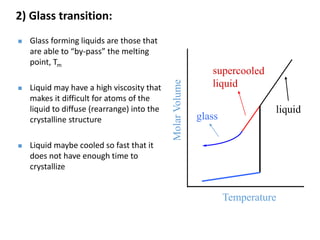
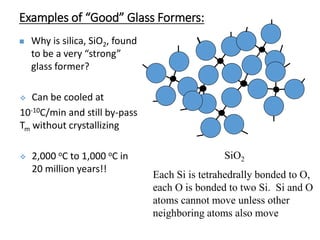
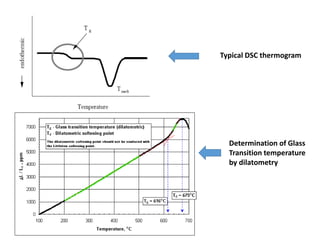
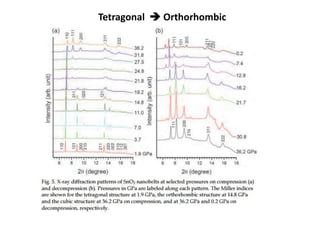
Phase transitions can be classified based on their order, mechanism, and thermodynamics. First order transitions involve a discontinuity in the first derivative of Gibbs free energy. Second order transitions have a continuous first derivative but discontinuity in the second derivative. Reconstructive transitions involve major structure reorganization while displacive transitions involve bond distortion. The kinetics of phase transitions involve nucleation and growth. Martensitic transformations occur via shear without diffusion. The BaTiO3 transition from cubic to tetragonal structure results in it becoming ferroelectric below 120°C. Glass transitions occur when liquids are cooled too fast to crystallize, becoming supercooled liquids called glasses.

1. Phase Transitions
By Saurav Chandra Sarma
CRYSTALLOGRAPHY AND IT’S APPLICATIONS

2. Outline
Introduction
Classification of Phase Transition
Kinetics of Phase Transition
Martensitic Transformation
BaTiO3 Phase Transition
Glass Transition
Other Examples
Conclusion

3. Introduction
• A phase transition is the transformation of
a thermodynamic system from one phase or state of
matter to another one by heat transfer.
• During a phase transition of a given medium certain
properties of the medium change, often discontinuously,
as a result of the change of some external condition, such
as temperature, pressure, or others
• For example, a liquid may become gas upon heating to
the boiling point, resulting in an abrupt change in volume.

4. Classification of Phase Transitions

5. Classification of
Phase
Transformations
Mechanism
Thermodynamics
Basedon
Ehrenfest, 1933
Buerger, 1951
Order of a phase transformation
B
A

6. Ehrenfest’s Classification
First order phase transition: Discontinuity in the first
derivative of Gibb’s Free Energy,G.
Second order phase transition: Continuous first
derivative but discontinuity in the second derivative of G.

8. Lambda Transition:

9. Buerger’s Classification
Reconstructive Transition: Involves a major reorganization
of the crystal structure.
E.g: Graphite Diamond
Displacive Transition:
Involves distortion of bond
rather than their breaking and
the structural changes.
E.g: Martensitic Transformation
Diffusional or Civilian
Military

10. Transformation involving first coordination
 Reconstructive (sluggish) DiamondGraphite
 Dilatational (rapid) Rock saltCsCl
Transformation involving second coordination
 Reconstructive (sluggish) QuartzCristobalite
 Displacive (rapid) LowHigh Quartz
Transformations involving disorder
 Substitutional (sluggish) LowHigh LiFeO2
 Rotational (rapid) FerroelectricParaelectric NH4H2PO4
Transformations involving bond type (sluggish)
GreyWhite Sn
Buerger’s Classification: full list

11. Liquid → Solid phase transformation
Solid (GS)
Liquid (GL)
Tm T →
G→
T
G
Liquid stableSolid stable
T - Undercooling
↑ t
“For sufficient
Undercooling”
 On cooling just below Tm solid becomes stable
 But solidification does not start
 E.g. liquid Ni can be undercooled 250 K below Tm
G → ve
G → +ve

12. Nucleation
of
 phase
Trasformation
 → 
+
Growth
till
 is
exhausted
=
1nd order
nucleation & growth
Kinetics of Phase Transition:

13. 13
Phase Transformations
Nucleation
• nuclei (seeds) act as templates on which crystals grow
• for nucleus to form rate of addition of atoms to nucleus must be
faster than rate of loss
• once nucleated, growth proceeds until equilibrium is attained
Driving force to nucleate increases as we increase T
– supercooling (eutectic, eutectoid)
– superheating (peritectic)
Small supercooling  slow nucleation rate - few nuclei - large crystals
Large supercooling  rapid nucleation rate - many nuclei - small crystals

14. Heterogeneous nucleation
 Nucleation occur at the interface between two phases or at the grain boundary.
Homogeneous nucleation
 Nucleation occur without any preferential nucleation sites.
 Occurs spontaneously and randomly but it requires superheating or
supercooling.
An example of supercooling: Pure water freezes at −42°C rather than at
its freezing temperature of 0°C. The crystallization into ice may be facilitated
by adding some nucleation “seeds”: small ice particles, or simply by shaking

15. 15
r* = critical nucleus: for r < r* nuclei shrink; for r >r* nuclei grow (to reduce energy)
Adapted from Fig.10.2(b), Callister & Rethwisch 8e.
Homogeneous Nucleation & Energy Effects
GT = Total Free Energy
= GS + GV
Surface Free Energy - destabilizes
the nuclei (it takes energy to make
an interface)
 2
4 rGS
 = surface tension
Volume (Bulk) Free Energy –
stabilizes the nuclei (releases energy)
 GrGV
3
3
4
volumeunit
energyfreevolume
 G

16. 16
Solidification
TH
T
r
f
m



2
*
Note: Hf and  are weakly dependent on T
 r* decreases as T increases
For typical T r* ~ 10 nm
Hf = latent heat of solidification
Tm = melting temperature
 = surface free energy
T = Tm - T = supercooling
r* = critical radius

17. Avirami equation:
 Transformations are often observed to follow a
characteristic S-shaped, or sigmoidal.
 Initial Slow rate time reqd. for forming a
significant no. of nuclei of the new phase.
 Intermediate fast rate  nuclei grow in size
and cross the critical radius
 Final slow rate particles already existing
begin to touch each other, forming a
boundary where growth stops.
The parameter ‘n’ depends on shape of β-
phase particles (the Dimension):
Spherical→ n=3 (3D)
Disk-shaped→ n=2 (2D)
Rod-shaped→ n=1 (1D)

18. Rate of Phase Transformation
Avrami equation => y = 1- exp (-ktn)
• k & n are transformation specific parameters
transformation complete
log t
Fractiontransformed,y
Fixed T
fraction
transformed
time
0.5
By convention rate = 1 / t0.5
Adapted from
Fig. 10.10,
Callister &
Rethwisch 8e.
maximum rate reached – now amount
unconverted decreases so rate slows
t0.5
rate increases as surface area increases
& nuclei grow

19. Temperature Dependence of Transformation
Rate
• For the recrystallization of Cu, since
rate = 1/t0.5
rate increases with increasing temperature
• Rate often so slow that attainment of equilibrium
state not possible!
Adapted from Fig.
10.11, Callister &
Rethwisch 8e.
(Fig. 10.11 adapted
from B.F. Decker and
D. Harker,
"Recrystallization in
Rolled Copper", Trans
AIME, 188, 1950, p.
888.)
135C 119C 113C 102C 88C 43C
1 10 102 104

20.  The martensitic transformation occurs without composition change
 The transformation occurs by shear without need for diffusion
 The atomic movements required are only a fraction of the interatomic
spacing
 The shear changes the shape of the transforming region
→ results in considerable amount of shear energy
→ plate-like shape of Martensite
 The amount of martensite formed is a function of the temperature to
which the sample is quenched and not of time
 Hardness of martensite is a function of the carbon content
→ but high hardness steel is very brittle as martensite is brittle
1) Martensitic Transformation:
Example
??

21. Martensite
FCC
Austenite
FCC
Austenite
Alternate choice of
Cell
Tetragonal
Martensite
Austenite to Martensite → 4.3 % volume increase
Possible positions of
Carbon atoms
Only a fraction of
the sites occupied
20% contraction of c-axis
12% expansion of a-axis
In Pure Fe after
the Matensitic transformation
c = a
C along the c-axis
obstructs the contraction
C
BCT
C
FCC Quench
%8.0
)('
%8.0
)( 
 
What happens
actually???

22. Martensite Austenite

23. 2) BaTiO3 Phase transition
>120oC
Click
me
Cubic Structure
(Paraelectric)
Tetragonal Strucure
(Ferroelectric)

24. Experimental Techniques:
• DSC
• EXAFS (Extended X-ray absorption fine structure)
• XANES (X-ray absorption near-edge structure)
• PDF (Pair Distribution Function)- To undertand local structure distortion.
Change in hysteresis
loop pattern
Source: Ferroelectricity, domain structure and phase transition of Barium Titanate,
Reviews of Modern Physics, 22,3 (1950)

25. Source: Ferroelectricity, domain structure and phase transition of Barium Titanate,
Reviews of Modern Physics, 22,3 (1950)

26. In the high-symmetry cubic
phase, no reflections are split.
In the tetragonal phase, (222)
remains a single peak whereas
the (400) reflection is divided
into (400/ 040) and (004) peaks
with an intensity ratio of 2:1
Source: J. AM. CHEM. SOC.,130, 22, (2008)

27. Tetragonal system: 10 Raman active
modes but 18 observed due to LO-TO
splitting.
Cubic system: Should be Raman inactive
but 2 modes observed due to displace Ti
position
Raman Spectra:

28.  Glass forming liquids are those that
are able to “by-pass” the melting
point, Tm
 Liquid may have a high viscosity that
makes it difficult for atoms of the
liquid to diffuse (rearrange) into the
crystalline structure
 Liquid maybe cooled so fast that it
does not have enough time to
crystallize
Temperature
MolarVolume
liquid
glass
2) Glass transition:

29. Examples of Poor Glass Formers:
 Why is water, H2O, found to be
a very “weak” glass former
 Requires cooling the liquid
faster than 1,000,000 oC/min
 300 to 150K in 9 milliseconds
H2O
No bonding between
molecules and molecules
can easily flow by each
other

30. Examples of “Good” Glass Formers:
 Why is silica, SiO2, found
to be a very “strong”
glass former?
 Can be cooled at
10-10C/min and still by-pass
Tm without crystallizing
 2,000 oC to 1,000 oC in
20 million years!!
SiO2
Each Si is tetrahedrally bonded to O,
each O is bonded to two Si. Si and O
atoms cannot move unless other
neighboring atoms also move

31. Typical DSC thermogram
Determination of Glass
Transition temperature
by dilatometry

32. Other Examples:

33. Tetragonal  Orthorhombic

34. Conclusion
• Experimental techniques used to understand the phase transition
depends on the type of phase transition.
• Depending on the type of transition, it shows various type of
complexity.
• Understanding of phase diagram is must to deal with phase
transition.