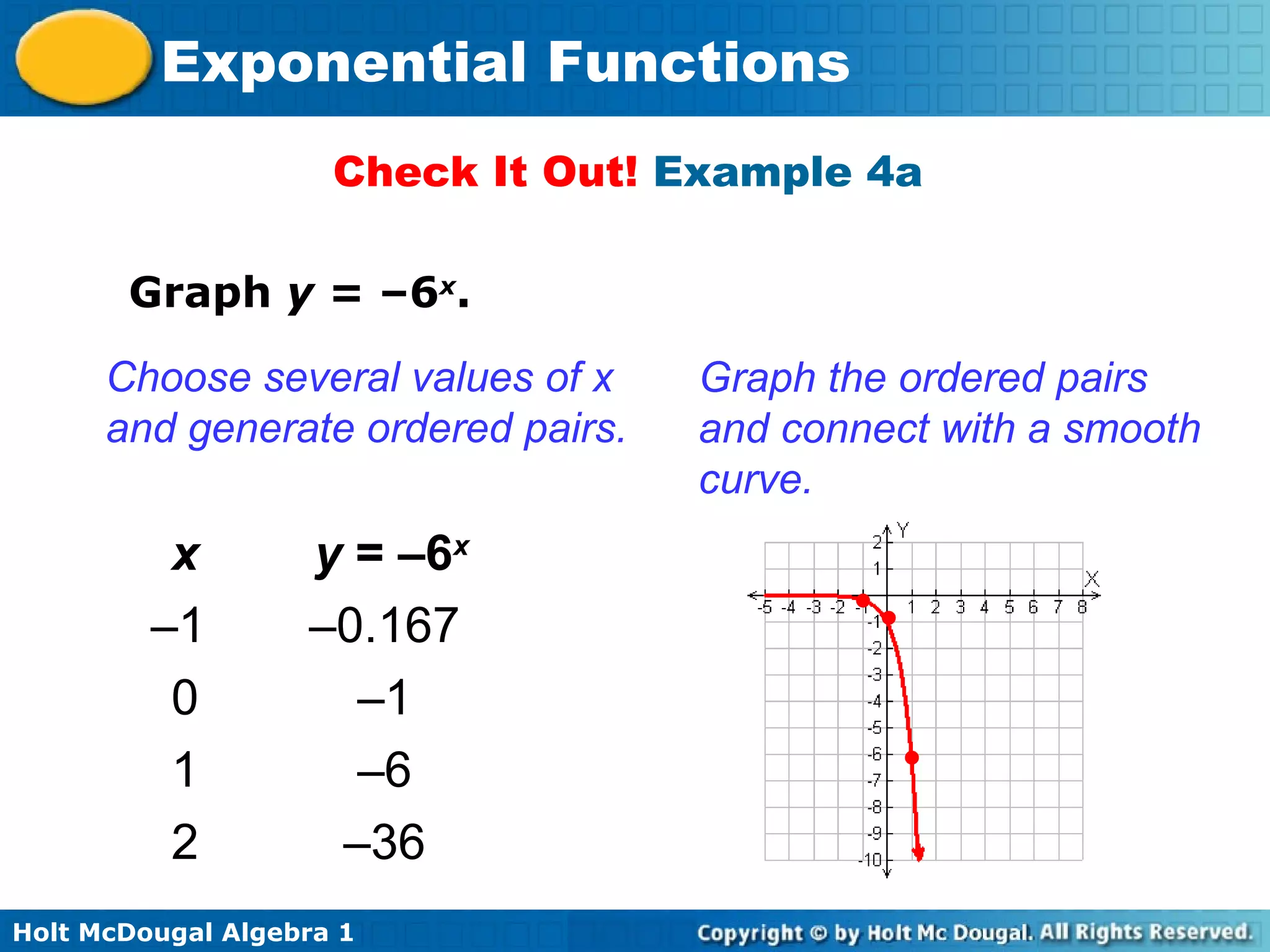
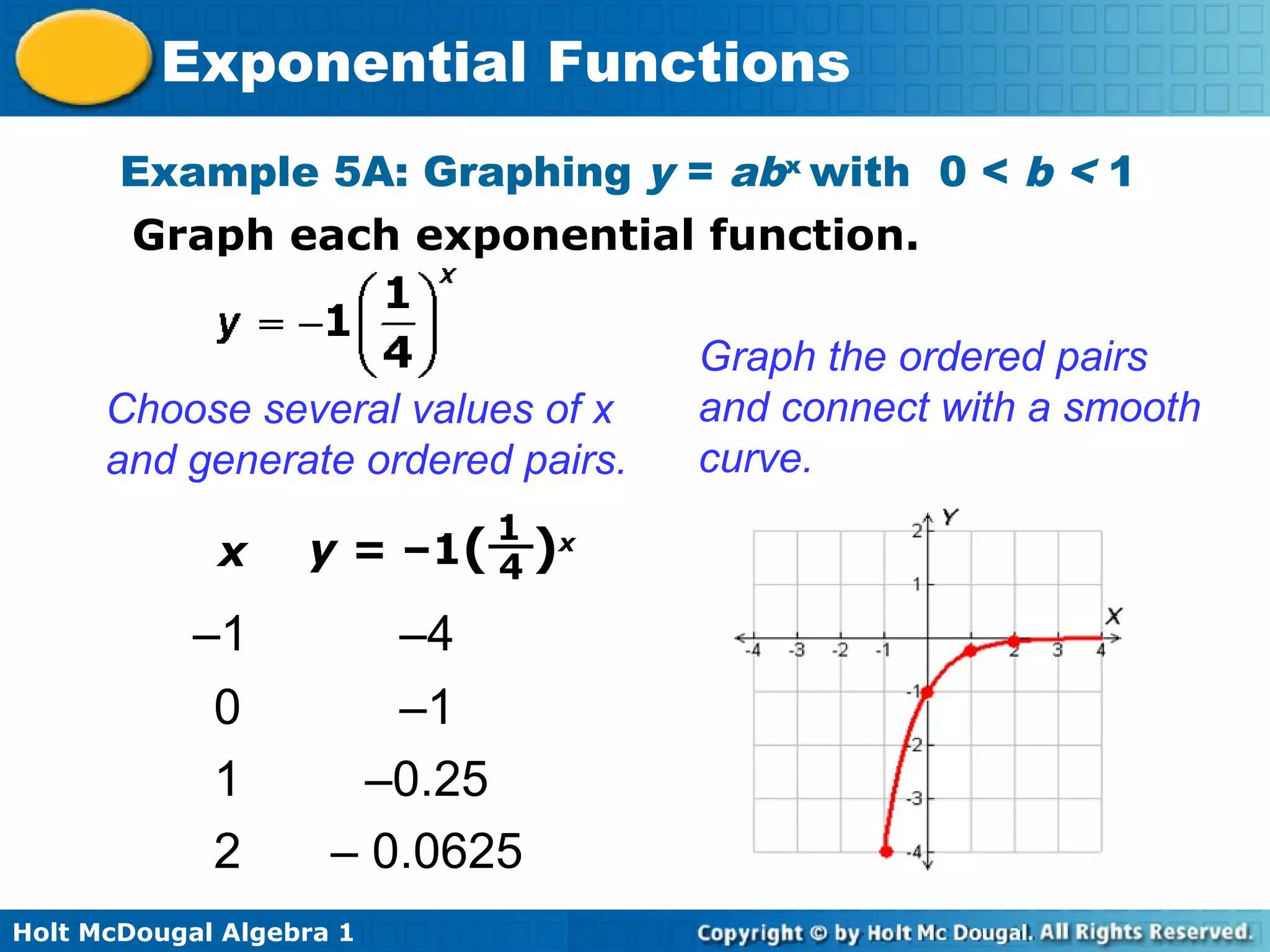
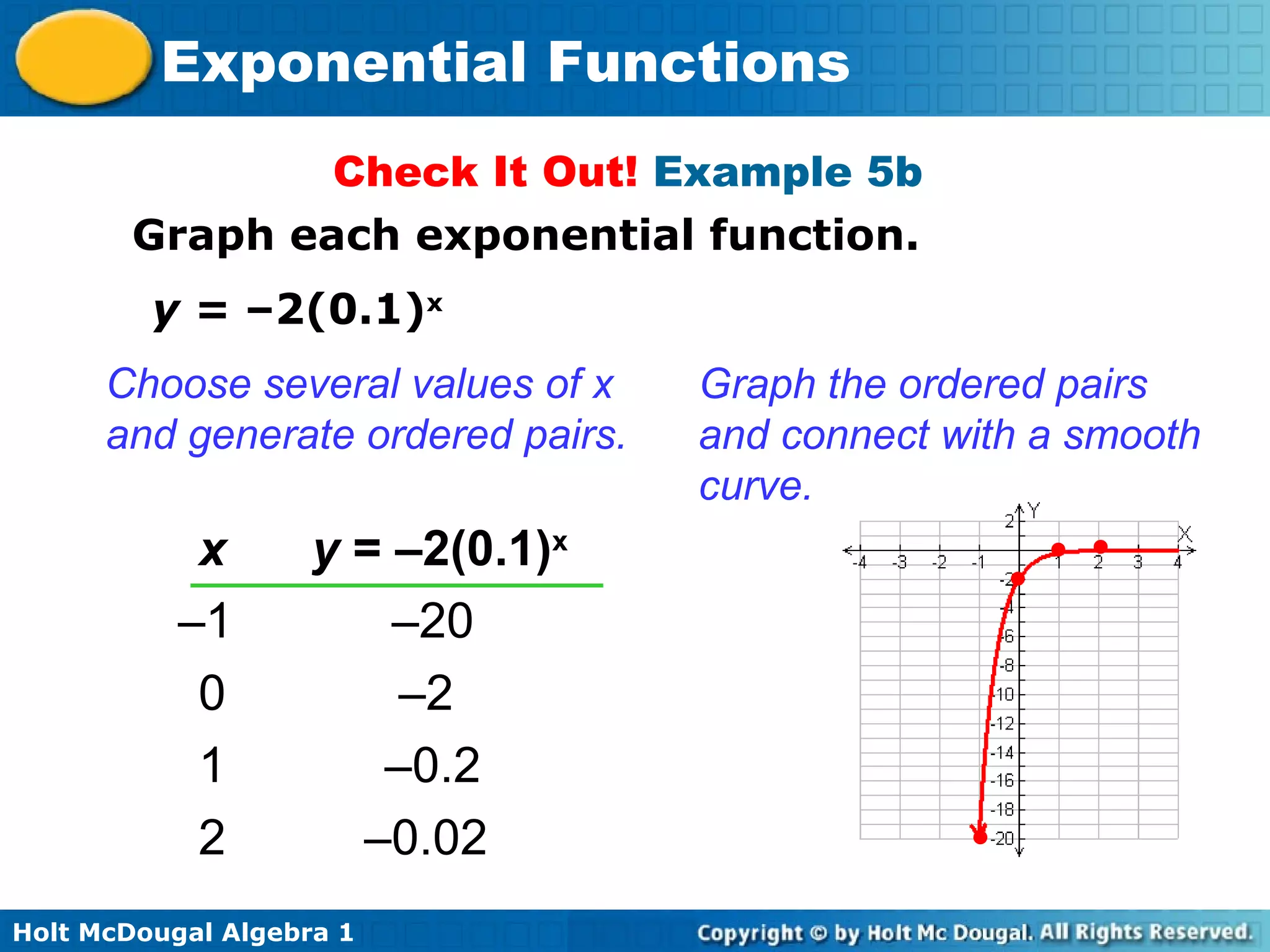
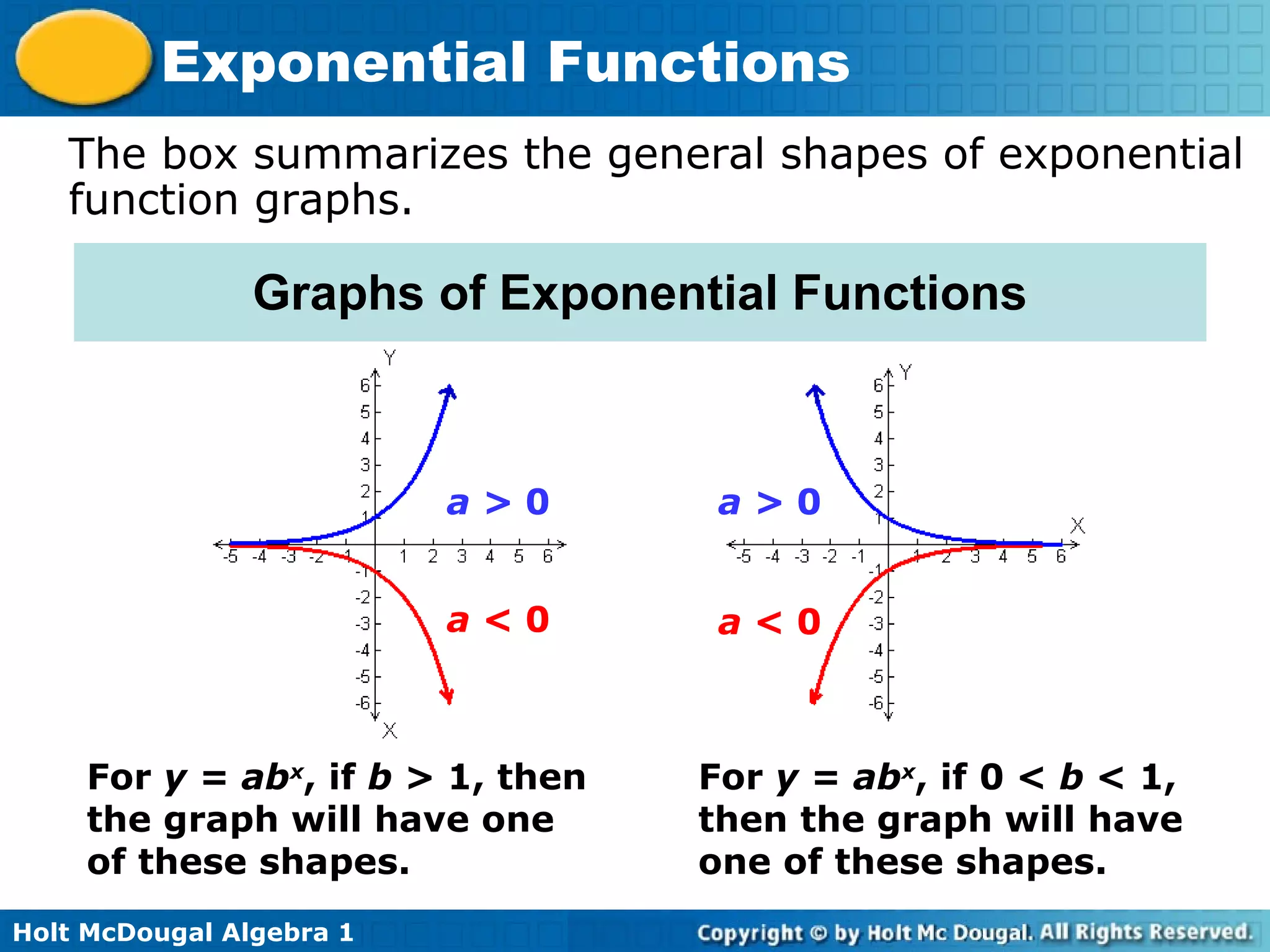
The document is from a Holt McDougal Algebra 1 textbook and covers exponential functions. It includes examples of evaluating, identifying, and graphing exponential functions. It also provides applications involving modeling population growth, money in a bank account, and car value depreciation using exponential functions. The key aspects of exponential functions discussed are that the independent variable appears as an exponent and the y-values are multiplied by a constant ratio as the x-values increase by a constant amount.