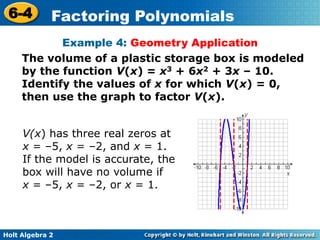
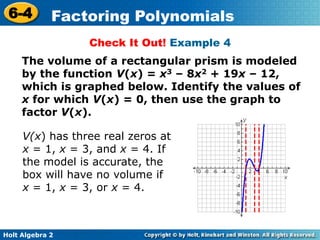
This document provides instruction on factoring polynomials. It begins with examples of factoring linear and quadratic expressions. It then discusses using the Factor Theorem and the Remainder Theorem to determine if a binomial is a factor of a polynomial. Additional examples demonstrate factoring polynomials by grouping like terms and using special rules to factor the sum and difference of cubes. An example applies these factoring techniques to model the volume of a storage box.

1. Holt Algebra 2
6-4 Factoring Polynomials6-4 Factoring Polynomials
Holt Algebra 2
Warm Up
Lesson Presentation
Lesson Quiz

2. Holt Algebra 2
6-4 Factoring Polynomials
Warm Up
Factor each expression.
1. 3x – 6y
2. a2 – b2
3. (x – 1)(x + 3)
4. (a + 1)(a2 + 1)
x2 + 2x – 3
3(x – 2y)
(a + b)(a – b)
a3 + a2 + a + 1
Find each product.

3. Holt Algebra 2
6-4 Factoring Polynomials
Use the Factor Theorem to determine
factors of a polynomial.
Factor the sum and difference of two
cubes.
Objectives

4. Holt Algebra 2
6-4 Factoring Polynomials
Recall that if a number is divided by any of its
factors, the remainder is 0. Likewise, if a
polynomial is divided by any of its factors, the
remainder is 0.
The Remainder Theorem states that if a
polynomial is divided by (x – a), the remainder
is the value of the function at a. So, if (x – a)
is a factor of P(x), then P(a) = 0.

5. Holt Algebra 2
6-4 Factoring Polynomials
Determine whether the given binomial is a factor
of the polynomial P(x).
Example 1: Determining Whether a Linear Binomial is
a Factor
A. (x + 1); (x2 – 3x + 1)
Find P(–1) by synthetic
substitution.
1 –3 1–1
–1
1 5–4
4
P(–1) = 5
P(–1) ≠ 0, so (x + 1)
is not a factor of
P(x) = x2 – 3x + 1.
B. (x + 2);
(3x4 + 6x3 – 5x – 10)
Find P(–2) by synthetic
substitution.
3 6 0 –5 –10–2
–6
3 0
1000
–500
P(–2) = 0, so (x + 2)
is a factor of P(x) =
3x4 + 6x3 – 5x – 10.

6. Holt Algebra 2
6-4 Factoring Polynomials
Check It Out! Example 1
Determine whether the given binomial is a factor
of the polynomial P(x).
a. (x + 2); (4x2 – 2x + 5)
Find P(–2) by synthetic
substitution.
4 –2 5–2
–8
4 25–10
20
P(–2) = 25
P(–2) ≠ 0, so (x + 2)
is not a factor of
P(x) = 4x2 – 2x + 5.
b. (3x – 6);
(3x4 – 6x3 + 6x2 + 3x – 30)
1 –2 2 1 –102
2
1 0
1040
520
P(2) = 0, so (3x – 6) is a
factor of P(x) = 3x4 – 6x3 +
6x2 + 3x – 30.
Divide the polynomial by 3,
then find P(2) by synthetic
substitution.

7. Holt Algebra 2
6-4 Factoring Polynomials
You are already familiar with methods for
factoring quadratic expressions. You can factor
polynomials of higher degrees using many of the
same methods you learned in Lesson 5-3.

8. Holt Algebra 2
6-4 Factoring Polynomials
Factor: x3 – x2 – 25x + 25.
Example 2: Factoring by Grouping
Group terms.(x3 – x2) + (–25x + 25)
Factor common monomials
from each group.
x2(x – 1) – 25(x – 1)
Factor out the common
binomial (x – 1).
(x – 1)(x2 – 25)
Factor the difference of
squares.
(x – 1)(x – 5)(x + 5)

9. Holt Algebra 2
6-4 Factoring Polynomials
Example 2 Continued
Check Use the table feature of your calculator to
compare the original expression and the factored
form.
The table shows that the original function and the
factored form have the same function values. 

10. Holt Algebra 2
6-4 Factoring Polynomials
Check It Out! Example 2a
Factor: x3 – 2x2 – 9x + 18.
Group terms.(x3 – 2x2) + (–9x + 18)
Factor common monomials
from each group.
x2(x – 2) – 9(x – 2)
Factor out the common
binomial (x – 2).
(x – 2)(x2 – 9)
Factor the difference of
squares.
(x – 2)(x – 3)(x + 3)

11. Holt Algebra 2
6-4 Factoring Polynomials
Check It Out! Example 2a Continued
Check Use the table feature of your calculator to
compare the original expression and the factored
form.
The table shows that the original function and the
factored form have the same function values. 

12. Holt Algebra 2
6-4 Factoring Polynomials
Check It Out! Example 2b
Factor: 2x3 + x2 + 8x + 4.
Group terms.(2x3 + x2) + (8x + 4)
Factor common monomials
from each group.
x2(2x + 1) + 4(2x + 1)
Factor out the common
binomial (2x + 1).
(2x + 1)(x2 + 4)
(2x + 1)(x2 + 4)

13. Holt Algebra 2
6-4 Factoring Polynomials
Just as there is a special rule for factoring the
difference of two squares, there are special rules for
factoring the sum or difference of two cubes.

14. Holt Algebra 2
6-4 Factoring Polynomials
Example 3A: Factoring the Sum or Difference of Two
Cubes
Factor the expression.
4x4 + 108x
Factor out the GCF, 4x.4x(x3 + 27)
Rewrite as the sum of cubes.4x(x3 + 33)
Use the rule a3 + b3 = (a + b)
 (a2 – ab + b2).
4x(x + 3)(x2 – x  3 + 32)
4x(x + 3)(x2 – 3x + 9)

15. Holt Algebra 2
6-4 Factoring Polynomials
Example 3B: Factoring the Sum or Difference of Two
Cubes
Factor the expression.
125d3 – 8
Rewrite as the difference
of cubes.
(5d)3 – 23
(5d – 2)[(5d)2 + 5d  2 + 22] Use the rule a3 – b3 =
(a – b)  (a2 + ab + b2).
(5d – 2)(25d2 + 10d + 4)

16. Holt Algebra 2
6-4 Factoring Polynomials
Check It Out! Example 3a
Factor the expression.
8 + z6
Rewrite as the difference
of cubes.
(2)3 + (z2)3
(2 + z2)[(2)2 – 2  z + (z2)2] Use the rule a3 + b3 =
(a + b)  (a2 – ab + b2).
(2 + z2)(4 – 2z + z4)

17. Holt Algebra 2
6-4 Factoring Polynomials
Check It Out! Example 3b
Factor the expression.
2x5 – 16x2
Factor out the GCF, 2x2.2x2(x3 – 8)
Rewrite as the difference of
cubes.
2x2(x3 – 23)
Use the rule a3 – b3 = (a – b)
 (a2 + ab + b2).
2x2(x – 2)(x2 + x  2 + 22)
2x2(x – 2)(x2 + 2x + 4)

18. Holt Algebra 2
6-4 Factoring Polynomials
Example 4: Geometry Application
The volume of a plastic storage box is modeled
by the function V(x) = x3 + 6x2 + 3x – 10.
Identify the values of x for which V(x) = 0,
then use the graph to factor V(x).
V(x) has three real zeros at
x = –5, x = –2, and x = 1.
If the model is accurate, the
box will have no volume if
x = –5, x = –2, or x = 1.

19. Holt Algebra 2
6-4 Factoring Polynomials
Use synthetic division to
factor the polynomial.
1 6 3 –101
1
1 0
V(x)= (x – 1)(x2 + 7x + 10)
107
107
Write V(x) as a product.
V(x)= (x – 1)(x + 2)(x + 5) Factor the quadratic.
Example 4 Continued
One corresponding factor is (x – 1).

20. Holt Algebra 2
6-4 Factoring Polynomials
Check It Out! Example 4
The volume of a rectangular prism is modeled
by the function V(x) = x3 – 8x2 + 19x – 12,
which is graphed below. Identify the values of
x for which V(x) = 0, then use the graph to
factor V(x).
V(x) has three real zeros at
x = 1, x = 3, and x = 4. If
the model is accurate, the
box will have no volume if
x = 1, x = 3, or x = 4.

21. Holt Algebra 2
6-4 Factoring Polynomials
Use synthetic division to
factor the polynomial.
1 –8 19 –121
1
1 0
V(x)= (x – 1)(x2 – 7x + 12)
12–7
12–7
Write V(x) as a product.
V(x)= (x – 1)(x – 3)(x – 4) Factor the quadratic.
Check It Out! Example 4 Continued
One corresponding factor is (x – 1).

22. Holt Algebra 2
6-4 Factoring Polynomials
4. x3 + 3x2 – 28x – 60
Lesson Quiz
2. x + 2; P(x) = x3 + 2x2 – x – 2
1. x – 1; P(x) = 3x2 – 2x + 5
8(2p – q)(4p2 + 2pq + q2)
(x + 3)(x + 3)(x – 3)3. x3 + 3x2 – 9x – 27
P(1) ≠ 0, so x – 1 is not a factor of P(x).
P(2) = 0, so x + 2 is a factor of P(x).
4. 64p3 – 8q3
(x + 6)(x – 5)(x + 2)