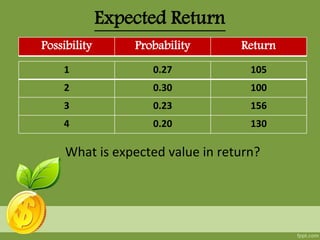
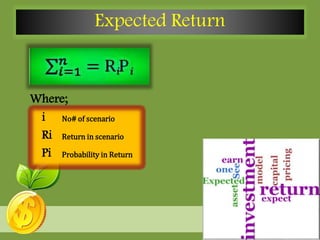
This document defines key concepts related to expected value, expected return, and standard deviation. It explains that expected value is the weighted average of all possible values of a random variable. Expected return is calculated by multiplying the probability and return of each possible scenario and summing the results. The document provides an example of calculating expected return using four scenarios. It also defines standard deviation as a measure of how spread out data is from the mean.

1. Expected value Return & standard
Deviation
Presented By: Jahanzeb Memon

2. • Expected Value
• Expected Return
• Probability
• Possibilities
• Standard Deviation
• Sums of Expected return & Standard Deviation

3. Expected Value:-
The expected value of a random variable is the weighted
average of all possible values that this random variable can
take on.
Expected value is another word for “Mean” or “Average.”
Expected Return:-
The expected return of a potential investment can be
computed by computing the product of the probability of a
given event and the return in that case and adding together
the products in each discrete scenario.

4. • Possibility:-
Possibility is something that may be true or might occur.
• Probability:-
Probability is defined as the likelihood of something
occurring or the chance of something happening.

5. Expected Return
Possibility Probability Return
1 0.27 105
2 0.30 100
3 0.23 156
4 0.20 130
What is expected value in return?

6. Expected Return
Where;
i No# of scenario
Ri Return in scenario
Pi Probability in Return

7. Expected Return
Possibility Probability Return
1 0.27 105
2 0.30 100
3 0.23 156
4 0.20 130
E (Ṝ) = (105*0.27)+(100*0.30)+(156*0.23)+(130*0.20)=
E (Ṝ) = 28.35 + 30 + 35.88 + 26 =
120.23

8. Standard Deviation:-
A measure of the dispersion of a set of data from its
mean. The more spread apart the data, the higher the
deviation. Standard deviation is calculated as the square
root of variance.

9. Standard Deviation

11. Thank You…