The document discusses risk and return in investments. It defines key concepts like holding period return (HPR), expected return, standard deviation, variance, and coefficient of variation. It provides examples of calculating HPR for stocks based on purchase price, selling price, and dividends. Expected return is the average HPR and can be calculated in different ways. Risk is the variability in returns and can be measured using standard deviation, variance, beta, etc. The document also discusses portfolio returns and how to calculate expected portfolio return based on individual asset expected returns and weights.

1. Unit-4
Risk and return
Risk and Return
Day – 1

2. Meaning of Return :
• Motivating force of Investment.
• Income received from investment or reward for investment.
• There are various types of returns.
• Basically we deal with Holding Period Return and Expected
Return in this unit.

3. Holding Period Return(HPR)
• Return that combines return realized from a change in the price of an
investment(capital gain) and cash receipt (Income) within a certain period.
• Holding period return as its name implies the total return realized in a holding
period that may be 1 day, 2 week, 1 month 1 year etc.
• Return in Rs. = Ending Price(P1)- Beginning Price(P0)+ Cash Receipt(C1)
• Rate of Return (r) =
𝑅𝑢𝑝𝑒𝑒 𝑟𝑒𝑡𝑢𝑟𝑛
𝐵𝑒𝑔𝑖𝑛𝑖𝑛𝑔 𝑃𝑟𝑖𝑐𝑒
𝑜𝑟
𝑃1−𝑃0+𝐶1
𝑃0
• If we have to choose the investment alternatives we should go for the
investment with Highest HPR.
• Before comparing we must calculate annualized HPR.
• Annualized HPR = 〖(1+HPR)〗^1/T−1 . Where T = holding period expressed in
year. T= 0.5 years for Holding Period of 6 months. i.e. 6 divided by 12 .

4. Example 1: Mr. Ram Purchased 300 shares of SBI at a market price of Rs. 200
per share. After one year SBI pays Rs. 10 in dividend per share and Mr. Ram sold
his share at a price of Rs. 240 per share after receiving dividend income.
Required: Holding Period Return
Solution:
Purchase Price (BP) = Rs. 200
Selling Price(EP) = Rs. 240
Dividend Income (C) = Rs. 10
Rupee return = EP – BP + C = 240 – 200 + 10 = Rs. 50 per share
=
𝐸𝑃−𝐵𝑃+𝐶
𝐵𝑃
Rate of Return
240−200+10
200
= = 0.25 or 25%
=
𝐷𝑖𝑣𝑖𝑑𝑒𝑛𝑑
𝐵𝑃
Dividend Yield = = 5%
10
200
=
𝐸𝑃 −𝐵𝑃
𝐵𝑃
Capital Gain Yield = =
240−200
200
20%
Hence, the rate of return made by Mr. Ram in this period is 25%. Out of this 25%, Dividend yield is 5% and
capital gain yield is 20%

5. Example 2: From the Following Data find Annual Rate of return(HPR)
Year
1998
1999
2000
2001
2002
2003
Stock Price
400
412
440
562
562
1500
Dividend
400
412
440
562
562
1500
Annual Return/ HPR
-
412−400+20
400
= 8%
440−412+20
412
= 11.65%

6. Expected Return , E(Rj) or (𝑅𝑗)
• Expected Return is the mean of Holding period Return.
• It is the return expected by investor in the future from investment.
• The calculation of expected rate of return is based on HPR of some periods.
• It is calculated in three ways:
• A. When historical HPR is given
• B. When probability distribution is given.
• C. When time value of money is to be considered.

7. Calculating E(Rj) when historical HPR’s are
given. State of Economy Moderate Recession Boom
HPR 20% 10% 3%
State
Moderate
Recession
Boom
HPR
20%
10%
3%
𝑯𝑷𝑹 = 𝟑𝟑%
Now,
Expected rate of Return of Assets I, E(Ri) =
𝐻𝑃𝑅
𝑁
=
33%
3
=11 %

8. Calculating E(Rj) when Probability distributions
are given State of Economy Moderate Recession Boom
HPR 20% 25% 30%
Probability 0.5 0.4 0.1
State
Moderate
Recession
Boom
HPR (R)
20%
25%
30%
𝑷 𝑿𝑹 = 𝟏𝟕%
Now,
Expected rate of Return of Assets I, E(Ri) = 𝑷 𝑿𝑹 = 𝟏𝟕%
P
20%
25%
30%
Px R
10%
4%
3%

9. Risk:
• Chances of some unfavourable event that will occur.
• In finance, risk refers to the variability in the return from an
investment.
• Possibility of earning less than expected earning is risk.
• The degree of risk can be measured via:
• Standard Deviation (𝜎)
• Variance (𝜎2
)
• Co-efficient of variation (CV)
• Beta co-efficient of Return

10. Standard Deviation (𝜎)
(Based on Historical data)
• Calculate the expected mean return of assets i.e E(RA)= 𝑅 =
𝑅
𝑁
• Subtract expected return from each possible outcome i.e RA- 𝑅𝐴
• Square the deviation and get a summation of those deviation i.e. (𝑅𝐴 − 𝑅)2
• Apply the formula
Standard deviation(𝜎) =
(𝑅𝑗−𝑅𝑗)
2
(𝑛−1)

11. Standard Deviation (𝜎)
(Based on probability)
• Calculate the expected mean return of assets i.e E(RA)= 𝑅 = 𝑃𝑅
• Subtract expected return from each possible outcome i.e RA- 𝑅𝐴
• Square the deviation and get a summation of those deviation i.e. (𝑅𝐴 − 𝑅)2
• Multiply the square of deviation by their respective probabilities and make
summation (𝑅𝑗 − 𝑅)2. 𝑃
• Apply the formula
Standard deviation(𝜎) = (𝑅𝑗 − 𝑅𝑗)2. 𝑃

12. Variance (𝜎2
)
• Higher the variance greater the degree of dispersion .
• Smaller variance, the lower the riskness of the stock.
Co-efficient of Variation(CV)
• Risk per unit of return.
• Higher CV denotes higher the risk and vice versa.
• CV =
𝜎𝑗
𝑅𝑗

13. Calculate:
a. Expected rate of Return b. Standard Deviation
c. Variance d. Co-efficient of Variation
State Probability Return
Boom 0.3 100%
Average 0.4 15%
Recession 0.3 -70%
State
Boom
Average
Recession
𝑷𝒊
0.3
0.4
0.3
𝑹𝒊
100%
15%
-70%
𝑷𝒊 x𝑹𝒊
30%
6%
-21%
𝑷𝒊 𝒙 𝑹𝒊 =
𝟏𝟓%
𝑹𝒊 − 𝑹𝒊
85%
0
-85%
a. Expected Return (𝑹𝒊) =
𝑷𝒊 𝒙 𝑹𝒊 = 𝟏𝟓%
(𝑹𝒊−𝑹𝒊)𝟐
7,225
0
7,225
𝑷𝒊 𝑿(𝑹𝒊 − 𝑹𝒊)𝟐
2,167.50
0
2167.5
𝑷𝒊 𝑿(𝑹𝒊 − 𝑹𝒊)𝟐 = 𝟒, 𝟑𝟑𝟓
b. Standard Deviation (𝜎) = (𝑅𝑗 − 𝑅𝑗)2× 𝑃𝑖 = 4,335 = 65. 84%
c. Variance (𝜎2
) = (65.84)2
= 4335
d. Coefficient of Varia𝑡𝑖𝑜𝑛 (𝐶𝑉) =
𝜎𝑗
𝑅𝑗
65.84%
15%
=
= 4.39

14. Consider the following historical data for A
and B:
Year RA RB
2010 20% 10%
2011 18% 12%
2012 -8% 14%
2013 22% 16%
Calculate:
a. Expected Return for both stocks
b. Standard Deviation and variance for both
stock.
c. Coefficient of variation for both stock.
d. Which stock may be appropriate for
investment why?
Answer:
a. 13 %, 13%
b. 14.095, 2.582
c. 1.0842, 0.1968
d. CV of stock B is lower than stock A. So, the Stock B seems more attractive
from investment due to less risk per unit.

15. Co-variance(𝐶𝑂𝑉𝑖𝑗)
• Statistical measure that shows the movement of two investment
or assets.
• Positive co-variance indicates that the return of two assets move
in same direction where as negative co-variance indicates that
return of two assets move in opposite direction.
• Zero Co-variance indicates that the return of two assets are
independent.
• 𝐶𝑂𝑉𝑖𝑗 =
(𝑅𝑖−𝑅𝑖)(𝑅𝑗−𝑅𝑗)
𝑛−1
or (𝑅𝑖 − 𝑅𝑖)(𝑅𝑗 − 𝑅𝑗).𝑃𝑖

16. Correlation (cor, r,𝜌)
• Measure of degree of relationship with which two variables move together.
• It lies between +1 and -1. +1 indicates that there is perfect positive
correlation and the return on two assets move on same direction with same
amount. -1 indicates that there is perfect negative relation and the return on
two assets move on opposite direction with same amount.
• Cor =
𝐶𝑂𝑉 𝐴𝐵
𝜎𝐴𝜎𝐵

17. Calculate:
a. Expected return on risk on Stock X and Y
b. Co-efficient of correlation and covariance
Probability Rx Ry
0.2 5% 30%
0.5 15% 20%
0.3 25% 10%
P
0.20
0.50
0.30
Rx
5%
15%
25%
Calculation of Expected return and standard deviation of stock X
Rx . Pi
1%
7.5%
7.5%
Rx . Pi = 16%
Rx- E(RX)
-11%
-1%
9%
(Rx- E(RX)2
121%
1%
81%
(Rx- E(RX)2 . Pi
24.2%
0.5%
24.3%
(Rx− E(RX)2 . Pi =
49%
a. Expected Return on X E(Rx) = 16%
b. Standard Deviation of Stock X (𝜎) = (Rx− E(RX)2 . Pi = 49% = 7%

18. Calculate:
a. Expected return on risk on Stock X and Y
b. Co-efficient of correlation and covariance
Probability Rx Ry
0.2 5% 30%
0.5 15% 20%
0.3 25% 10%
P
0.20
0.50
0.30
Ry
30%
20%
10%
Calculation of Expected return and standard deviation of stock Y
Ry . Pi
6%
10%
3%
Ry . Pi = 19%
Ry- E(Ry)
11%
1%
-9%
(Ry- E(Ry)2
121%
1%
81%
(Ry- E(Ry)2 . Pi
24.2%
0.5%
24.3%
(Ry− E(Ry)2 . Pi = 49%
a. Expected Return on Y E(Ry) = 19%
b. Standard Deviation of Stock Y (𝜎) = (Ry− E(Ry)2 . Pi = 49% = 7%

19. Calculate:
a. Expected return on risk on Stock X and Y
b. Co-efficient of correlation and covariance
Probability Rx Ry
0.2 5% 30%
0.5 15% 20%
0.3 25% 10%
P
0.20
0.50
0.30
Calculation of coefficient of correlation and covariance
(Ry- E(Ry))
11%
1%
-9%
(Rx- E(RX)). (Ry- E(Ry)) . PI
-24.2%
-0.5%
-24.35
(Rx− E(RX)). (Ry− E(Ry)) .Pi= -49%
a. Covariance of return ( COVXY)
b. Co-efficient of correlation (CORxy) = = = -1
(Rx- E(RX))
-11%
-1%
9%
= (Rx− E(RX)). (Ry− E(Ry)) .Pi
= −49%
𝐶𝑂𝑉𝑋𝑌
𝜎𝑋. 𝜎𝑌
−49%
7𝑋 7

20. Consider the given information :
Year Return on NIC market Return on market
1 7.5% 17%
2 22.8% 14%
3 0 5.8%
4 -9.9% -7
5 0.6% 5.6
a. Based on Historical rate of return data, calculate the expected return on
common stock of NIC and on market.
b. Calculate standard deviation of the return of stock on NIC and on market.
c. Calculate the covariance and correlation coefficient of the return on NIC and
market.

21. Portfolio:
• Simply Defined as the combination of investments in various
securities.
• Portfolio is created to minimize the risk of investment with higher
return.
• Portfolio Theory was proposed by Harry Markowitz in 1952s.
• Markowitz Model is based on following assumptions:
• Investors are risk averse.
• All investors have same expected single period investment horizon.
• Investors base their investment decision on the expected return and
standard deviation of returns.

22. Portfolio Return , E(Rp) or 𝑅𝑝
• Portfolio return refers to the return on total investment when an
investor invests in more than one assets or security.
• We can find the Portfolio return by using following formula:
• E(Rp) = 𝑅𝑖 × 𝑊𝑖 or it is the sum of product of weight and return
of individual assets
• E(Rp) = E(RA) x WA + E(RB) x WB or, 𝑅𝑝. 𝑃𝑖
• The total weight must be 100% or 1. If the weight is not given in
the question. We need to calculate the weight
• Wi =
𝐹𝑢𝑛𝑑 𝑖𝑛𝑣𝑒𝑠𝑡𝑒𝑑 𝑖𝑛 𝐴𝑠𝑠𝑒𝑡𝑠
𝑇𝑜𝑡𝑎𝑙 𝐼𝑛𝑣𝑒𝑠𝑡𝑚𝑒𝑛𝑡

23. Calculate the
expected portfolio
return:
Company Investment Expected
Retrun
A Rs. 1,20,000 10%
B Rs. 2,00,000 12%
C Rs. 40,000 6%
Company
A
B
C
Investmet
1,20,000
2,00,000
40,000
E(R)
10%
12%
6%
Weight(W)
0.3333
0.5555
0.1112
Total Investment = 120000+200000+40000 = 3,60,000
Weight of A (WA) =
𝟏𝟐𝟎𝟎𝟎𝟎
𝟑𝟔𝟎𝟎𝟎𝟎
= 0.3333 or 33.33 %
Weight of B (WB) =
2,00000
360000
= 0.5555 or 55.55 %
Weight of C (WC) = 1- 0.3333-0.5555 or 100% - 33.33% - 55.55% = 0.1112 or 11.12%
E(R) x W
3.33%
6.66%
0.66 %
𝑬 𝑹 𝒙 𝑾 = 𝟏𝟎. 𝟔𝟓%

24. Calculate the
expected portfolio
return:
Company Investment Expected
Retrun
A Rs. 1,20,000 10%
B Rs. 2,00,000 12%
C Rs. 40,000 6%
Alternative Solution:
=
E(RP) = E(RA) x WA + E(RB) x WB + E(RC) x WC
10% x
1,20,000
3,60,000
+ 12% x
2,00,000
3,60,000
+ 6% x
40,000
3,60,000
= 10.67%

25. You own a portfolio that has invested Rs. 40,000 in Stock A and Rs.
60,000 in Stock B. if the expected returns on these stocks are 10% and
20% respectively. What is the expected return on the portfolio?
Answer is given in your text book. ( Illustration 4.6)

26. Portfolio Risk (𝜎𝑃)
• Aggregate risk of assets included in the portfolio.
• It is not the weighted average of standard deviation of individual securities included
in portfolio.
• The portfolio risk does not depend only upon the risk of individual risk but also on
the relationship(correlation and covariance) between return of two assets.
• 𝜎𝑝 = 𝜎𝐴
2
. 𝑊𝐴
2
+ 𝜎𝐵
2
𝑊𝐵
2
+ 2𝑊𝐴. 𝑊𝐵𝐶𝑜𝑟𝐴𝐵𝜎𝐴𝜎𝐵 OR 𝜎𝐴
2
. 𝑊𝐴
2
+ 𝜎𝐵
2
𝑊𝐵
2
+ 2𝑊𝐴. 𝑊𝐵𝐶𝑜𝑣𝐴𝐵
• Or, [𝑅𝑃 − 𝐸(𝑅𝑃)]2. 𝑃𝑖 (If probability is given )
• 𝑉𝑎𝑟𝑖𝑎𝑛𝑐𝑒 𝑜𝑓 𝑜𝑓 𝑝𝑜𝑟𝑡𝑓𝑜𝑙𝑖𝑜 = 𝜎𝑝
2 CV of portfolio =
𝜎𝑝
𝑅𝑝

27. Methods to calculate Portfolio return
• Find Expected return of
individual assets.
• Find standard deviation of each
assets.
• Find covariance of two assets.
• Use the formula of portfolio
standard deviation which
includes covariance
• Find individual portfolio return
RP by using formula WA.RA+ WB.RB
• Multiply the Rp with probability
and get summation. Which is
expected portfolio return E(Rp).
• Find [Rp-E(Rp)]2.Pi
• Use the formula
[Rp−E(Rp)]2.Pi and get
portfolio standard deviation.

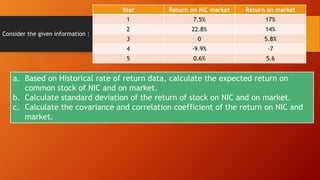
28. Consider the given information and answer the questions:
a. Calculate the expected rate of return for each stock and portfolio if
equal amount of money is invested in each stock.
b. Calculate standard deviation for each stock
Scenario P
Rate of Return
Stock A Stock B
Recession 0.3 5% 30%
Normal 0.40 10 20
Boom 0.30 15 10
Scenario
Recession
Normal
Boom
Pi
0.3
0.4
0.3
RA
5%
10
15
RB
30%
20
10
RA.Pi RB.Pi
Expected Return on Stock A, E(RA) = 𝑅𝐴. 𝑃𝐼
Expected Return on Stock B, E(RB) = 𝑅𝐵. 𝑃𝐼
Expected Return on Portfolio, E(Rp) = WA E(RA) + WB. E(RB)
Since equal amount is invested in both stocks WA= WB= 0.5
[RA – E(RA)] [RA – E(RA)]2.PI
Standard Deviation of stock A, (𝜎𝐴) = [RA – E(RA)]2.PI

29. Consider the given information and answer the questions:
a. Calculate the expected rate of return for each stock and portfolio if
equal amount of money is invested in each stock.
b. Calculate standard deviation for each stock
Scenario P
Rate of Return
Stock A Stock B
Recession 0.3 5% 30%
Normal 0.40 10 20
Boom 0.30 15 10
Scenario
Recession
Normal
Boom
Pi
0.3
0.4
0.3
[RB – E(RB)] [RB – E(RB)]2.PI
Standard Deviation of stock B, (𝜎𝐵) = [RB – E(RB)]2.PI
Standard Deviation of Portfolio, (𝜎𝑝) = 𝜎𝐴
2
. 𝑊𝐴
2
+ 𝜎𝐵
2
𝑊𝐵
2
+ 2𝑊𝐴. 𝑊𝐵𝐶𝑜𝑣𝐴𝐵
Where COVAB= (𝑅𝐴 − 𝑅𝐴)(𝑅𝐵 − 𝑅𝐵).𝑃𝑖
[RA – E(RA)] [RB – E(RB)]

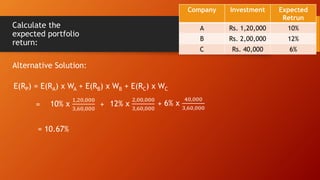
30. Consider the given information and answer the questions:
a. Calculate the expected rate of return for each stock and portfolio if
equal amount of money is invested in each stock.
b. Calculate standard deviation for each stock
Scenario P
Rate of Return
Stock A Stock B
Recession 0.3 5% 30%
Normal 0.40 10 20
Boom 0.30 15 10
Scenario
Recession
Normal
Boom
Pi
0.3
0.4
0.3
RA
5%
10
15
RB
30%
20
10
RP= 0.5xRA+ O.5 x RB
0.5 x 5 + 0.5 x 30 = 17.5
0.5 x 10 + 0.5 x 20 = 15
0.5 x 15 + 0.5 x 10 = 12.5
ALTERNATIVE SOLUTION :
RP.Pi
17.5 x 0.3 = 5.25
15 x 0.4 = 6
12.5 x 0.3 = 3.75
E(Rp) = 𝑹𝑷. 𝑷𝑰 = 15%
Expected Return on portfolio E(Rp) = 𝑹𝑷. 𝑷𝑰 = 15%
Now, Find [Rp- E(Rp)] it’s square and multiply with Pi to get [𝑅𝑃 − 𝐸(𝑅𝑃)]2. 𝑃𝑖
Portfolio standard deviation (𝜎𝑃) = [𝑅𝑃 − 𝐸(𝑅𝑃)]2. 𝑃𝑖

31. NOTE:
• when the correlation between assets is perfectly negative it
is possible to eliminate risk.
• When the correlation between assets is perfectly positive
there is not risk diversifying benefit of the portfolio.
• When the correlation is less than 1, it is possible to reduce
the portfolio risk but it would not be eliminated.

32. Types of Investor According to Risk
Perception
• Risk indifference/ Risk Neutral:
• Investor who does not consider risk while choosing investment.
• This type of investor tries to balance the rate of return and risk
associated with same investment.
• Risk Averse / Risk Averter:
• Investor who demands more return for the small increment in risk.
• He selects the higher return alternative with identical risk.
• Risk Seeker/ Risk Lover/Risk Taker:
• Investor who believes that greater risk provide higher return .
• He selects the higher risk alternative with identical return.

33. Beta Coefficient (𝛽𝑖):
• Investment contains risk. Those risk can be diversifiable(and undiversifiable.
• Diversifiable risk is also called unsystematic risk which is created by internal
factors of an organization such as lack of capital, inefficiency of manger etc.
• Undiversifiable risk is also called systematic risk which is created by external
factors such as inflation, change in interest rates etc.
• Unsystematic risk can be eliminated with efficiency of organization but
systematic risk cannot be elilmated.
• Systematic risk thus should be assessed and its effect should be minimized.
• The statistical tool that measures the systematic risk of an assets in relation to
the market is beta coefficient.

34. Beta Coefficient (𝛽𝑖):
• Beta coefficient (𝛽𝑖) =
𝐶𝑜𝑣𝑖𝑚
𝜎𝑚
2 or
𝐶𝑜𝑟𝑖𝑚 .𝜎𝑖
𝜎𝑚
2
• Portfolio Beta (𝛽𝑝) = 𝛽𝑖. 𝑊𝑖
• The Beta co-efficient of market is always assumed to be 1. Market
refers to the stock market such as NEPSE.
• If beta co-efficient is greater than 1, such stock is regarded as
aggressive stock meaning to say, the stock is riskier than the market.
• If the beta co-efficient is less than 1 , such stock is regarded as
defensive stock and considered to be less riskier than the market.

35. Practice Problem Prob Rm Rj
0.3 15% 20%
0.4 9% 5%
0.4 18% 12%
The market and the stock J have the following probabilites distribution
Where, Rm= required rate of return on a portfolio consisting of all
stocks, which is the market portfolio
Rj= Required rate of return on stock j.
a. Calculate the expected rates of returns for the market and stock J
b. Calculate the standard deviation for the market and stock J
c. Calculate the co-efficient of variation for the market and stock J
d. Interpret all the above result.
a. Expected return on stock = 11.6% Expected return on market = 13.5%
b. Standard deviation on stock = 6.216%, S.D. on market = 3.85
c. Calculate the co-efficient of variation for the market and stock J
d. Interpret all the above result.

36. Analyzing the Risk and Return
Capital Assets Pricing Model(CAPM)
• A model that helps to calculate the required rate of return to overcome the risk associated with it.
• This Model helps and investor to estimate the return in accordance to the risk associated with it.
• This model suggests the following relationship between required rate and risk relationship.
• Ri = Rf + (Rm-Rf)𝛽i
• Where Ri = Required rate of return,
Rm = Expected rate of return
Rf = Risk free Rate
Rm = Expected return on market.
Rm – Rf = Market risk premium
𝛽i= Beta Co-efficient
• The relationship between an assets return and its systematic risk can be expressed by CAPM, which
is called Security Market Line(SML).
• SML is a way to represent CAPM graphically.