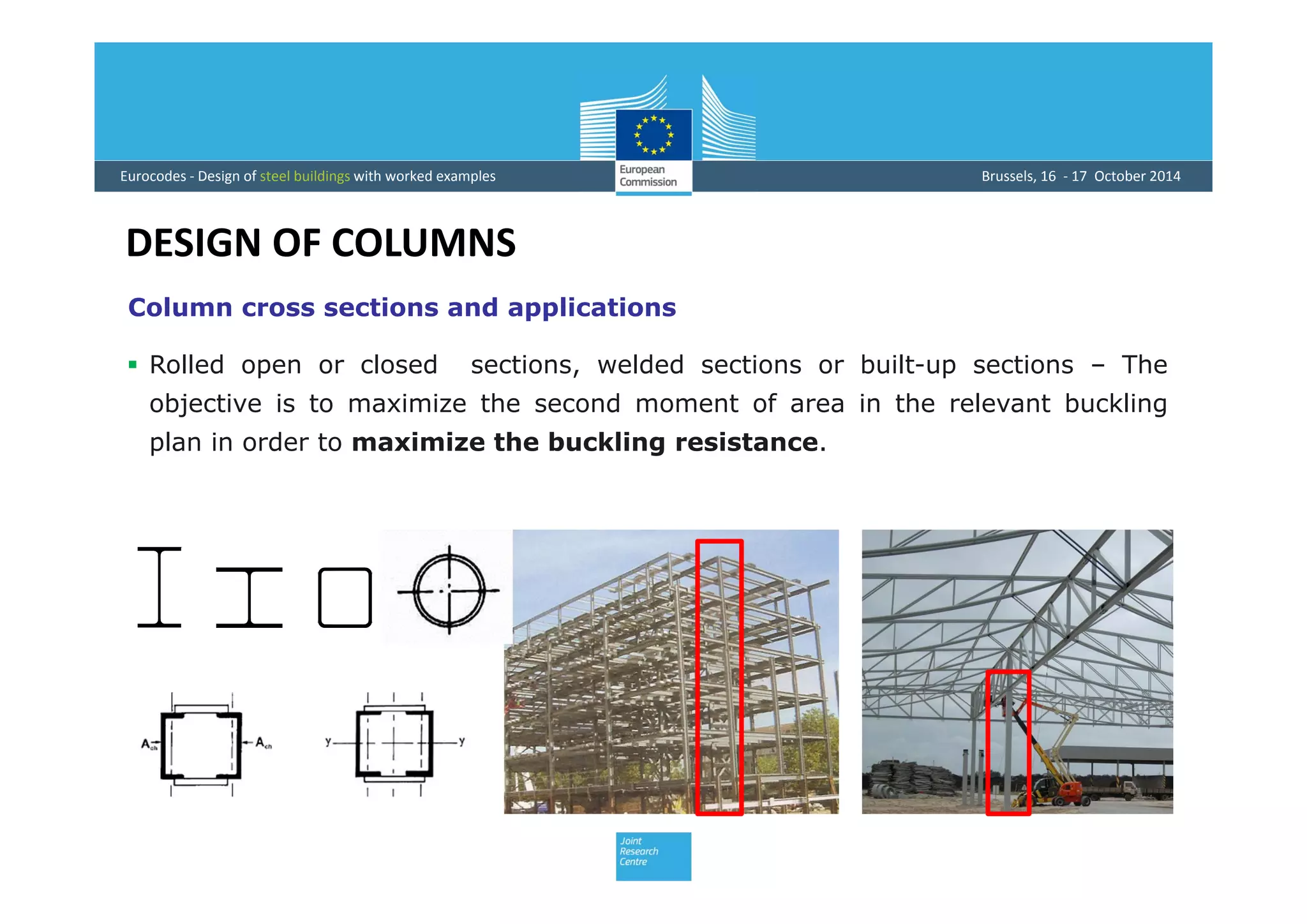
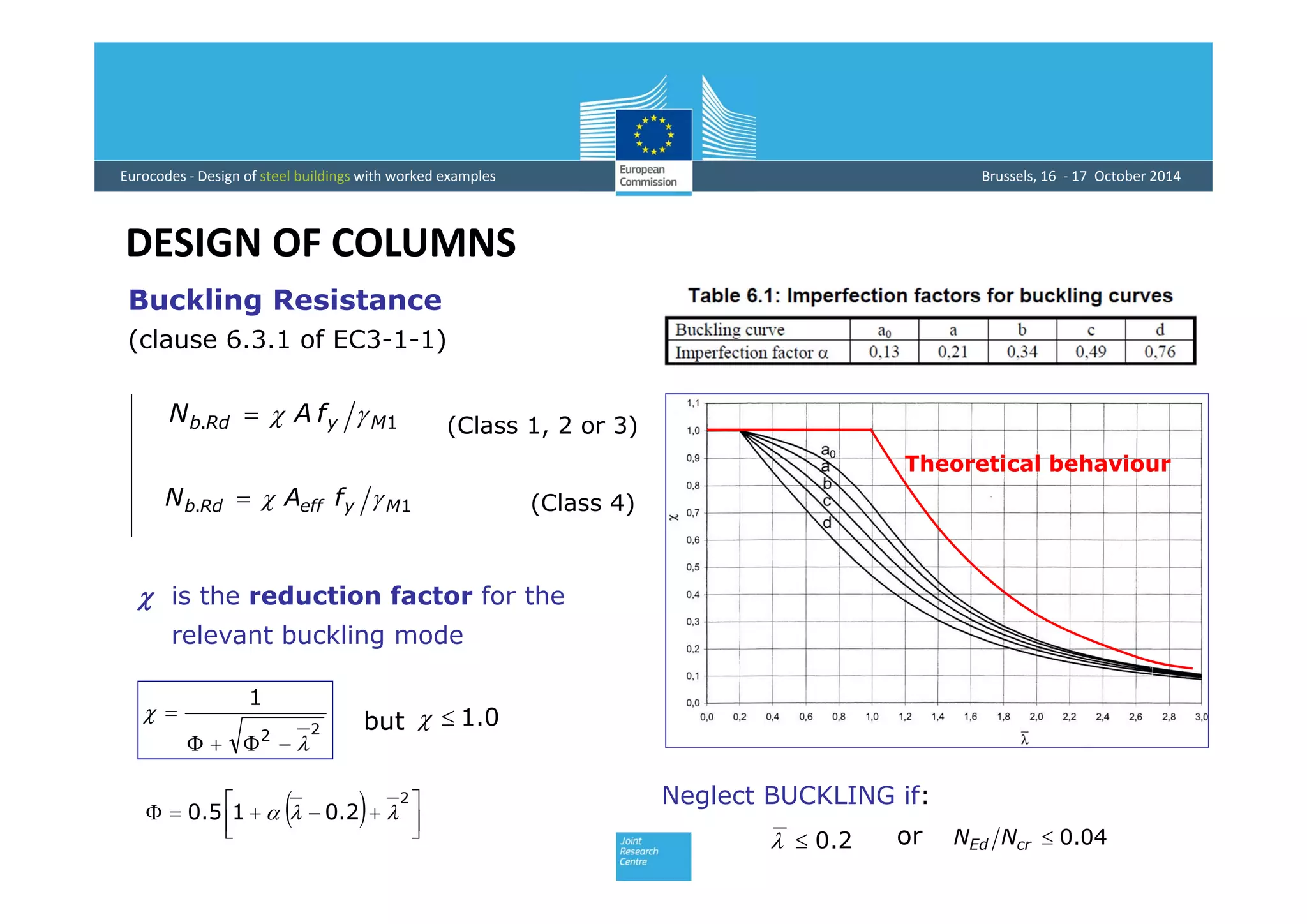
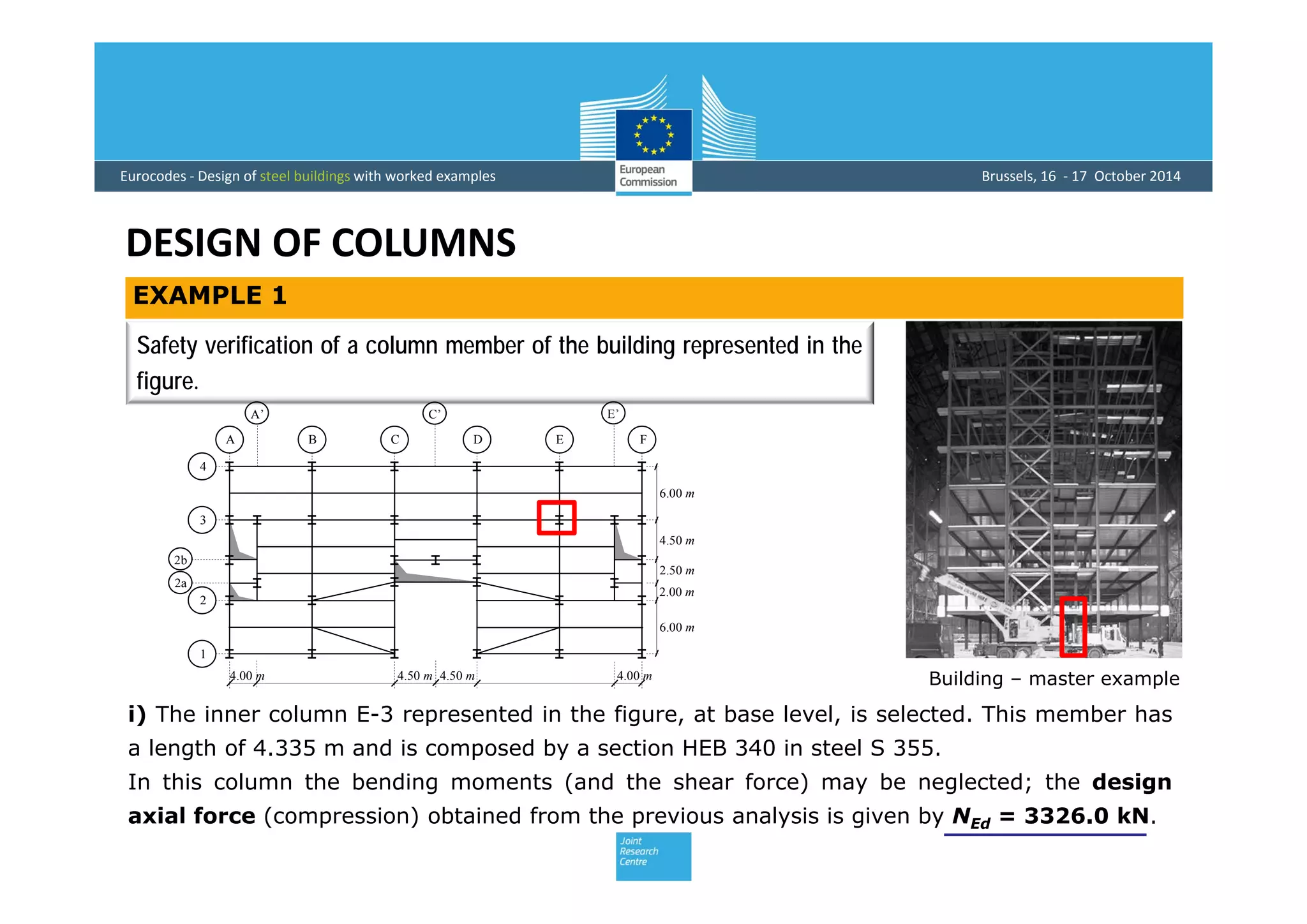
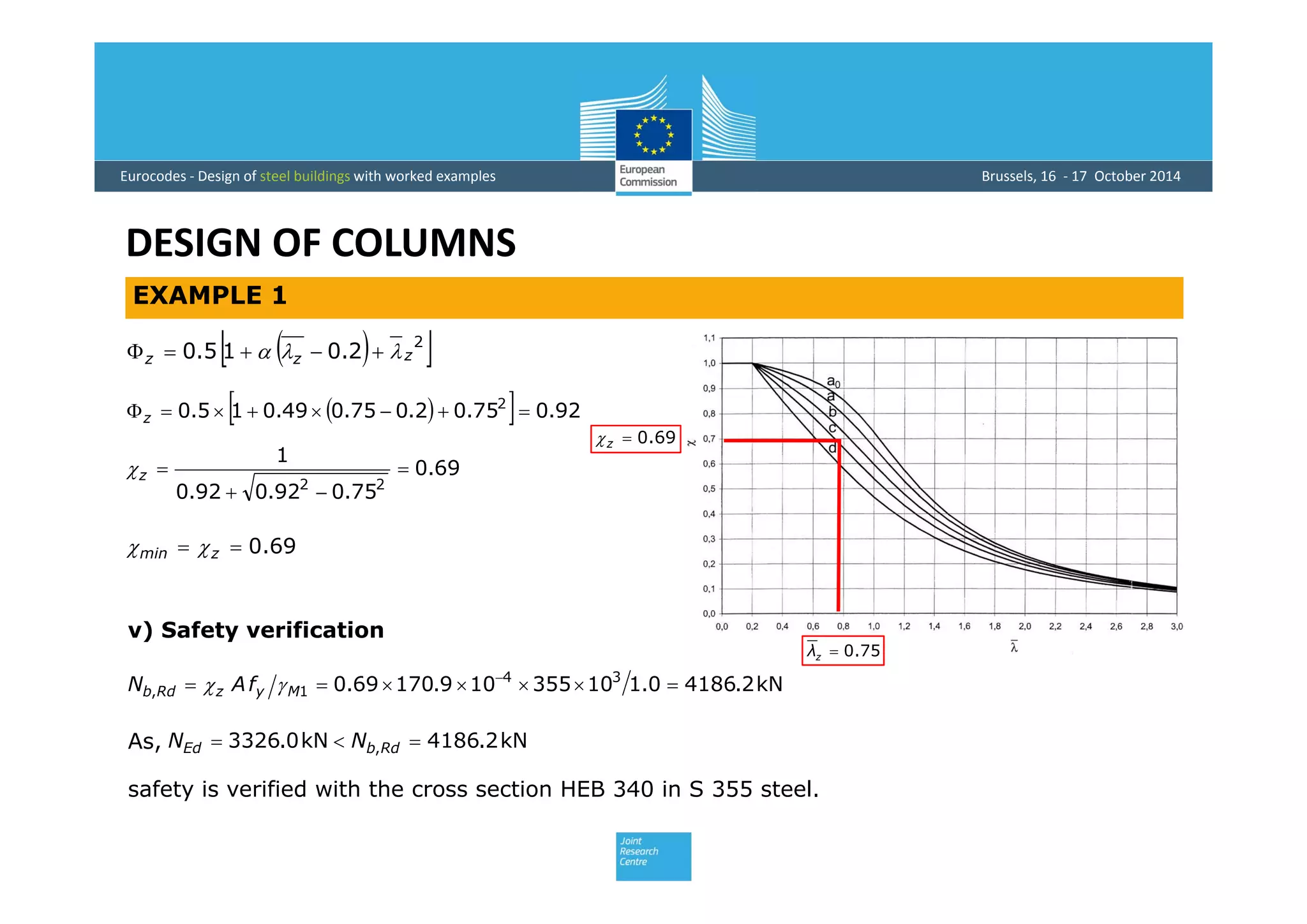
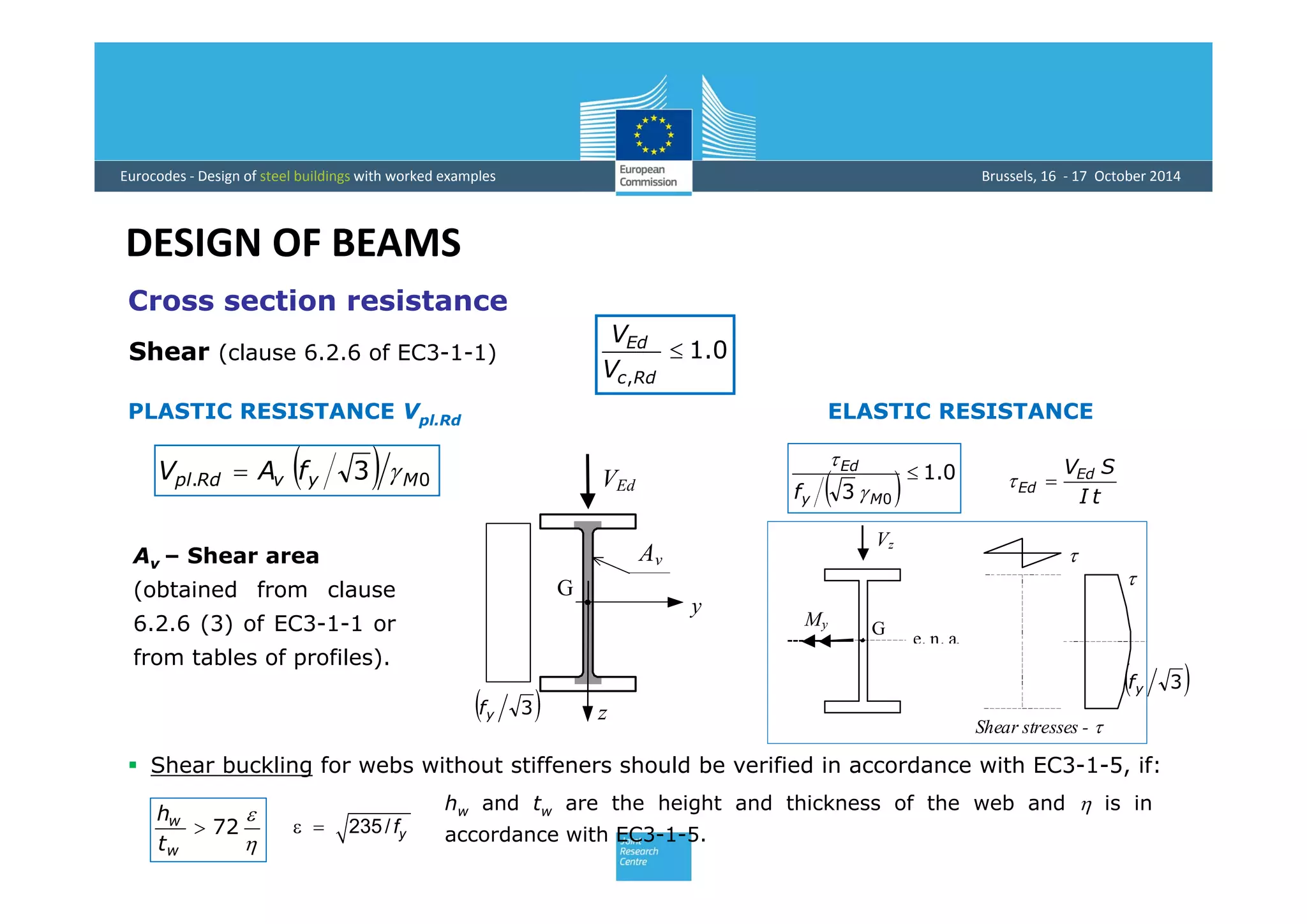
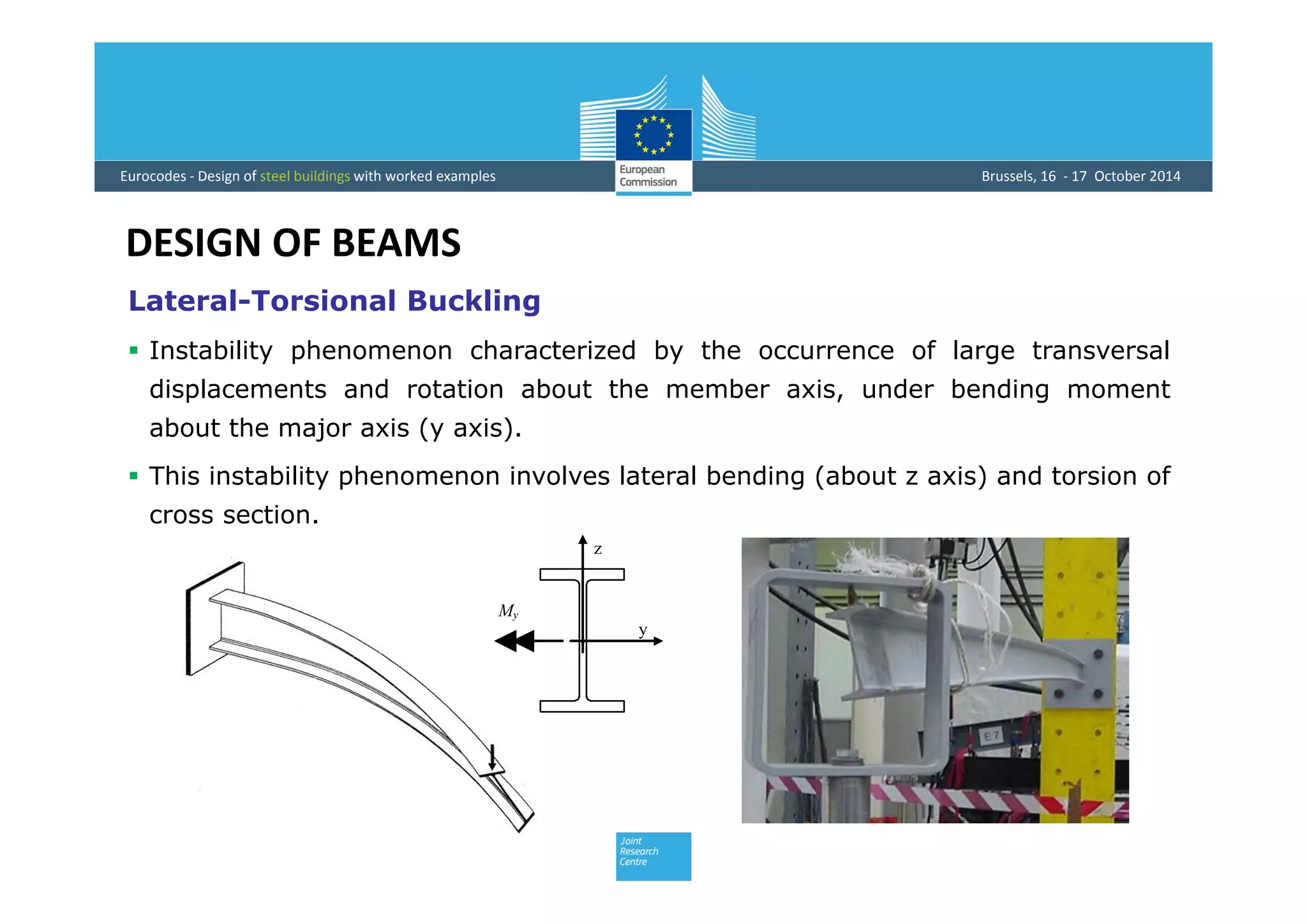
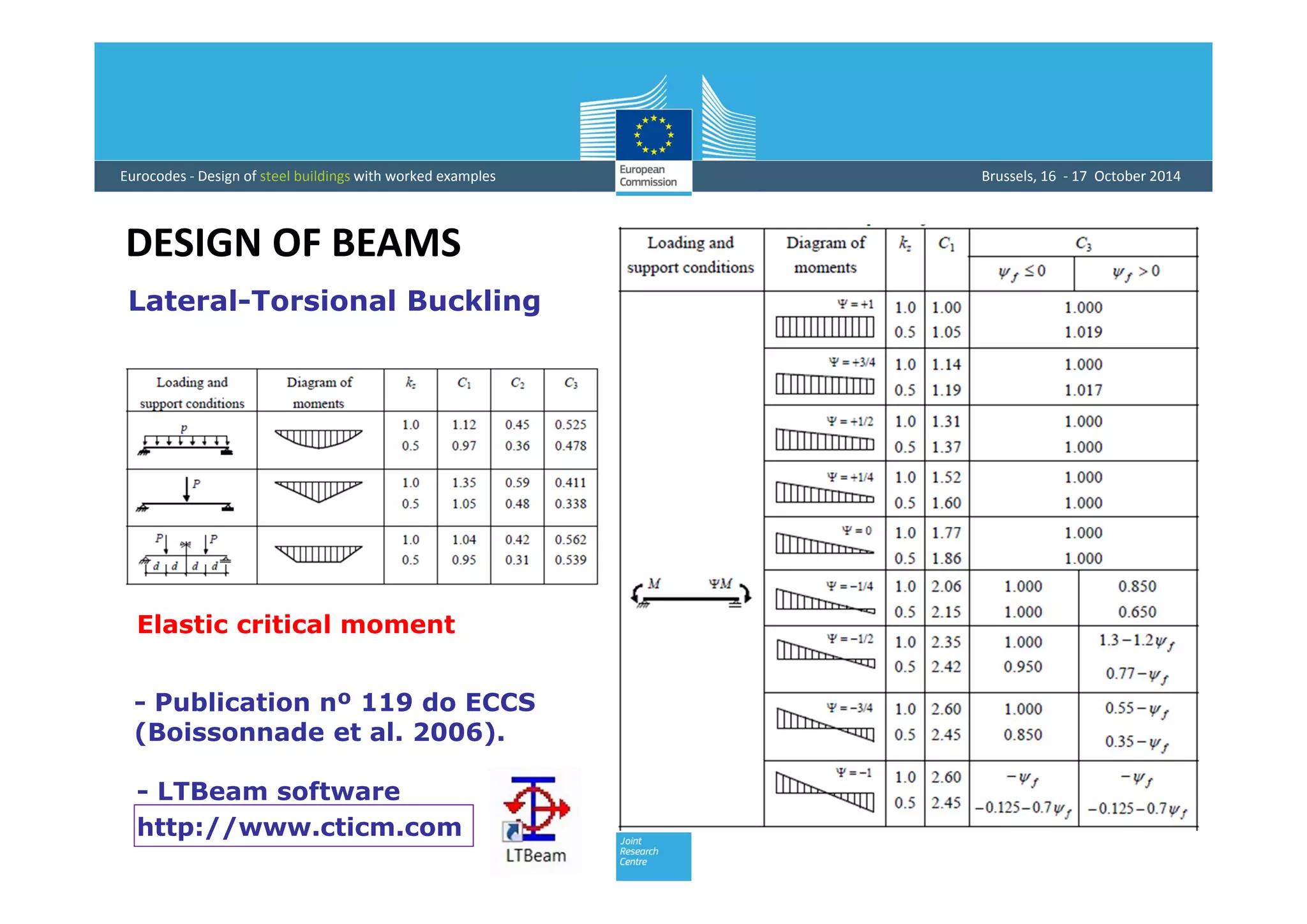
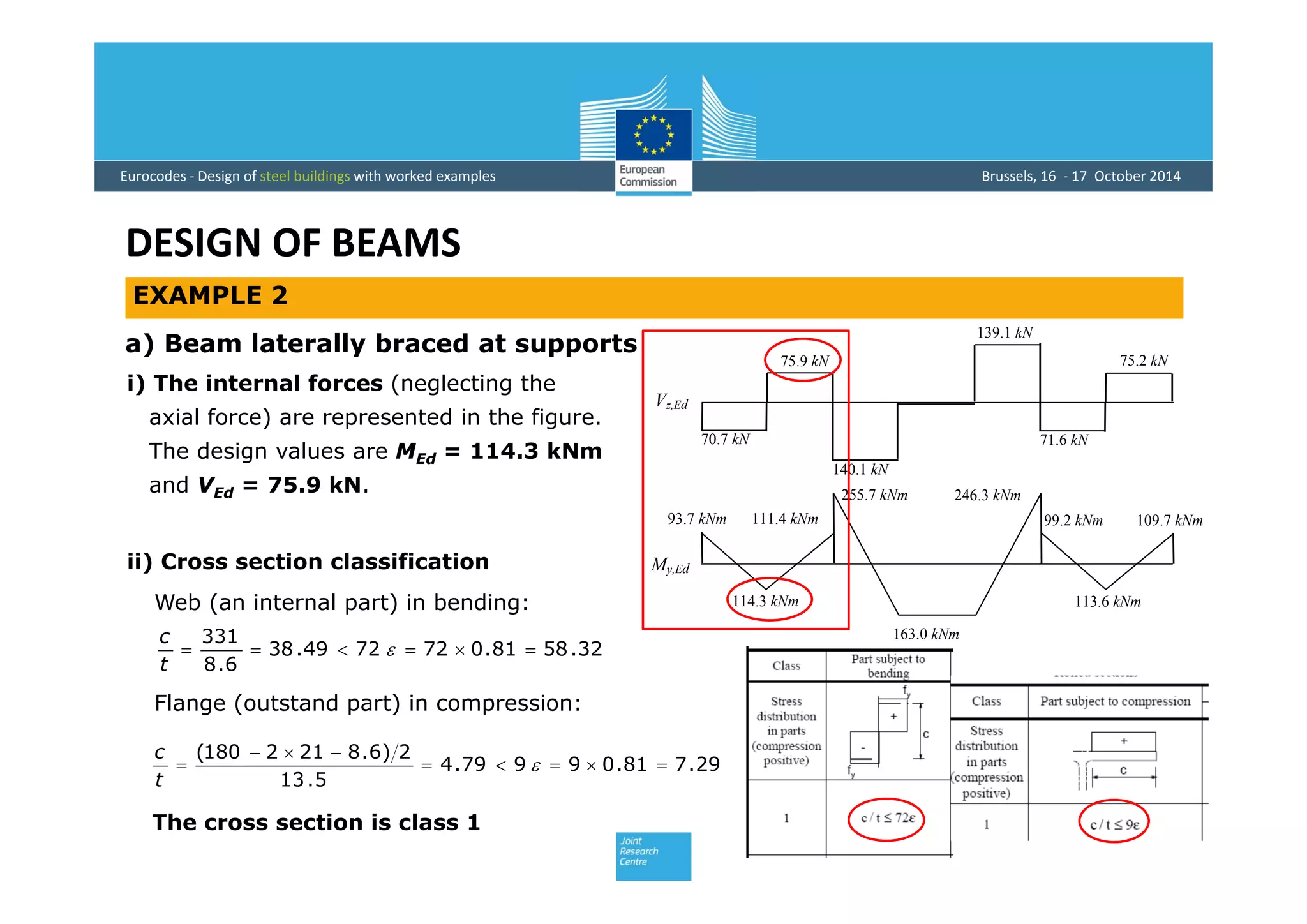
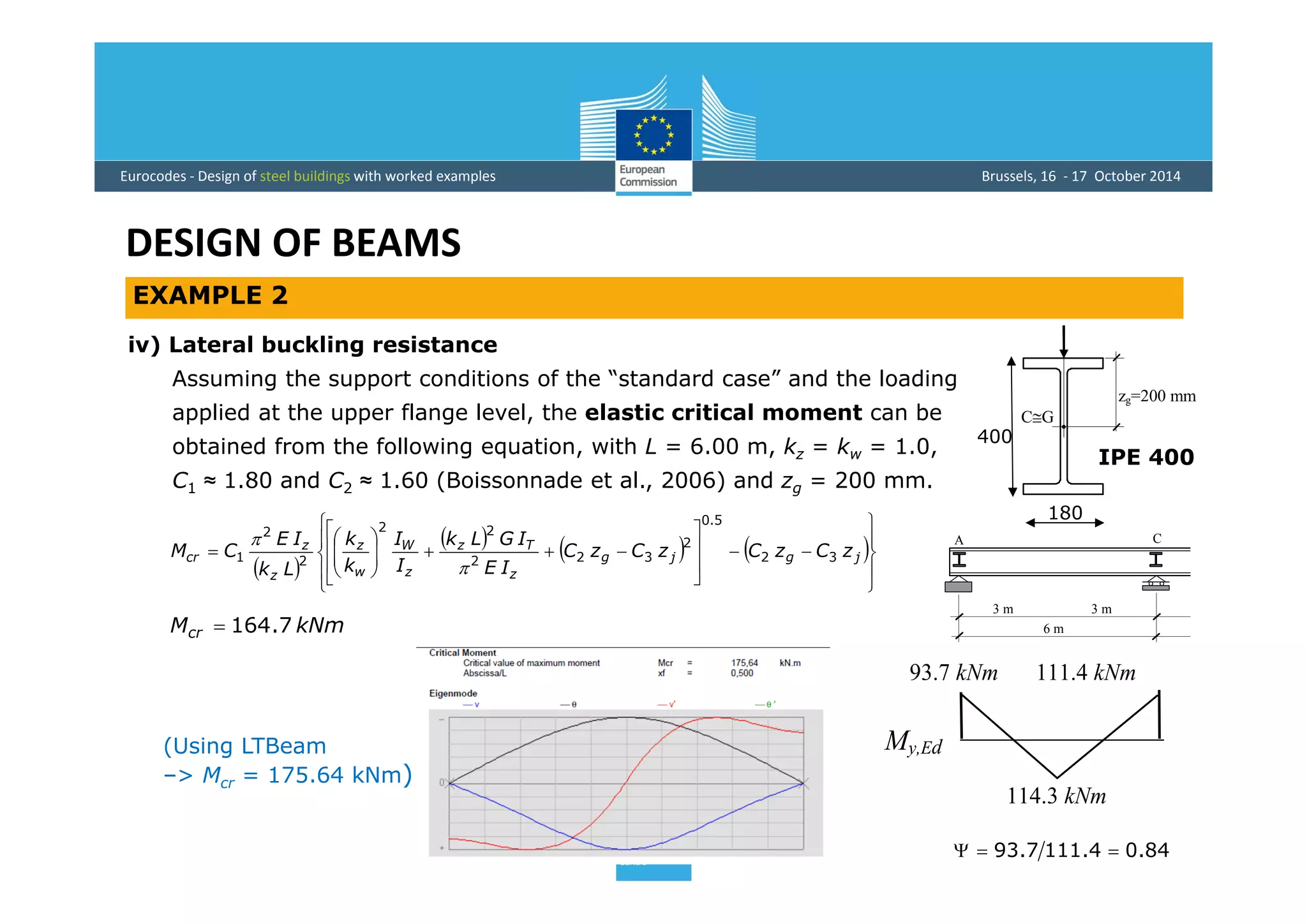
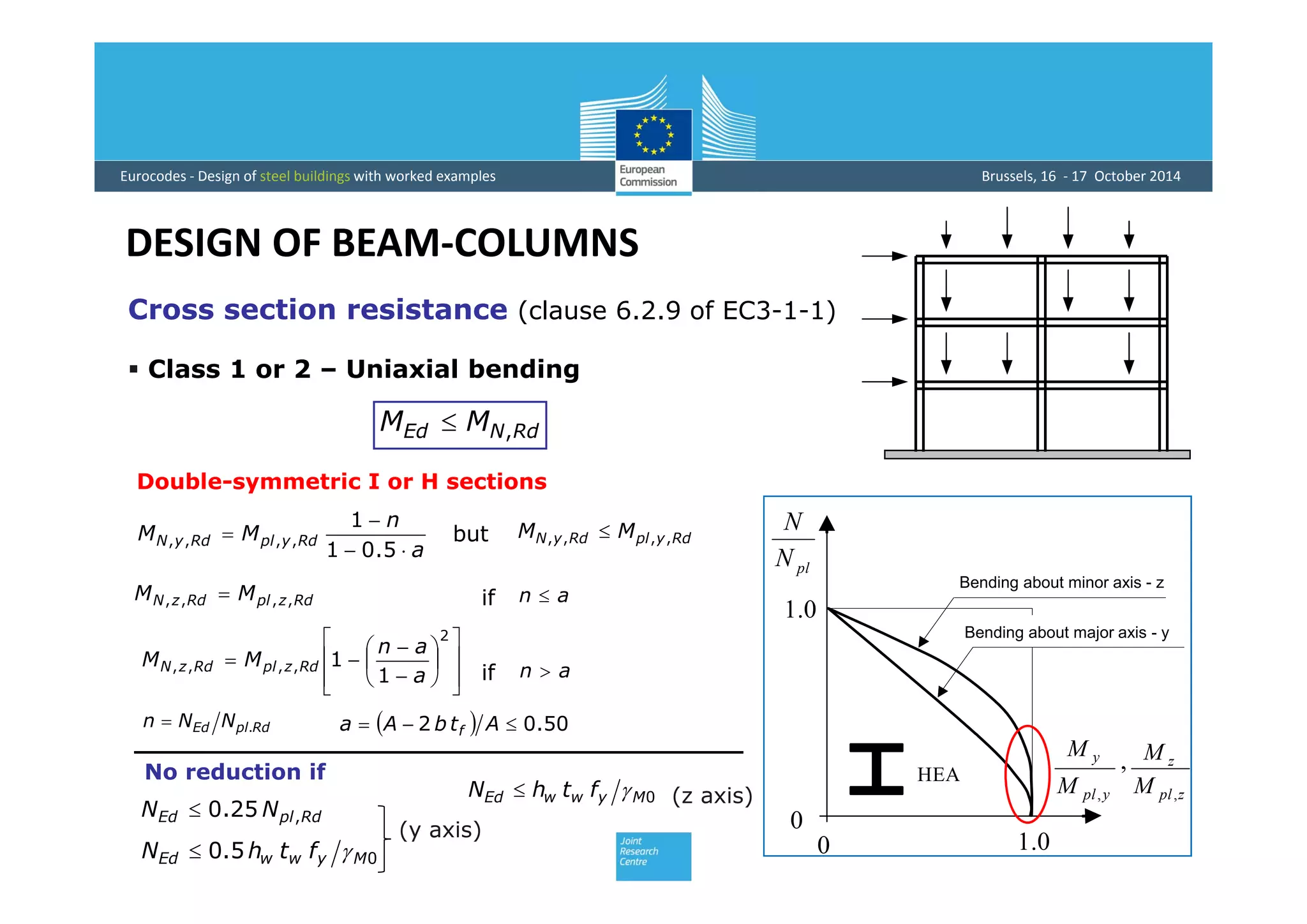
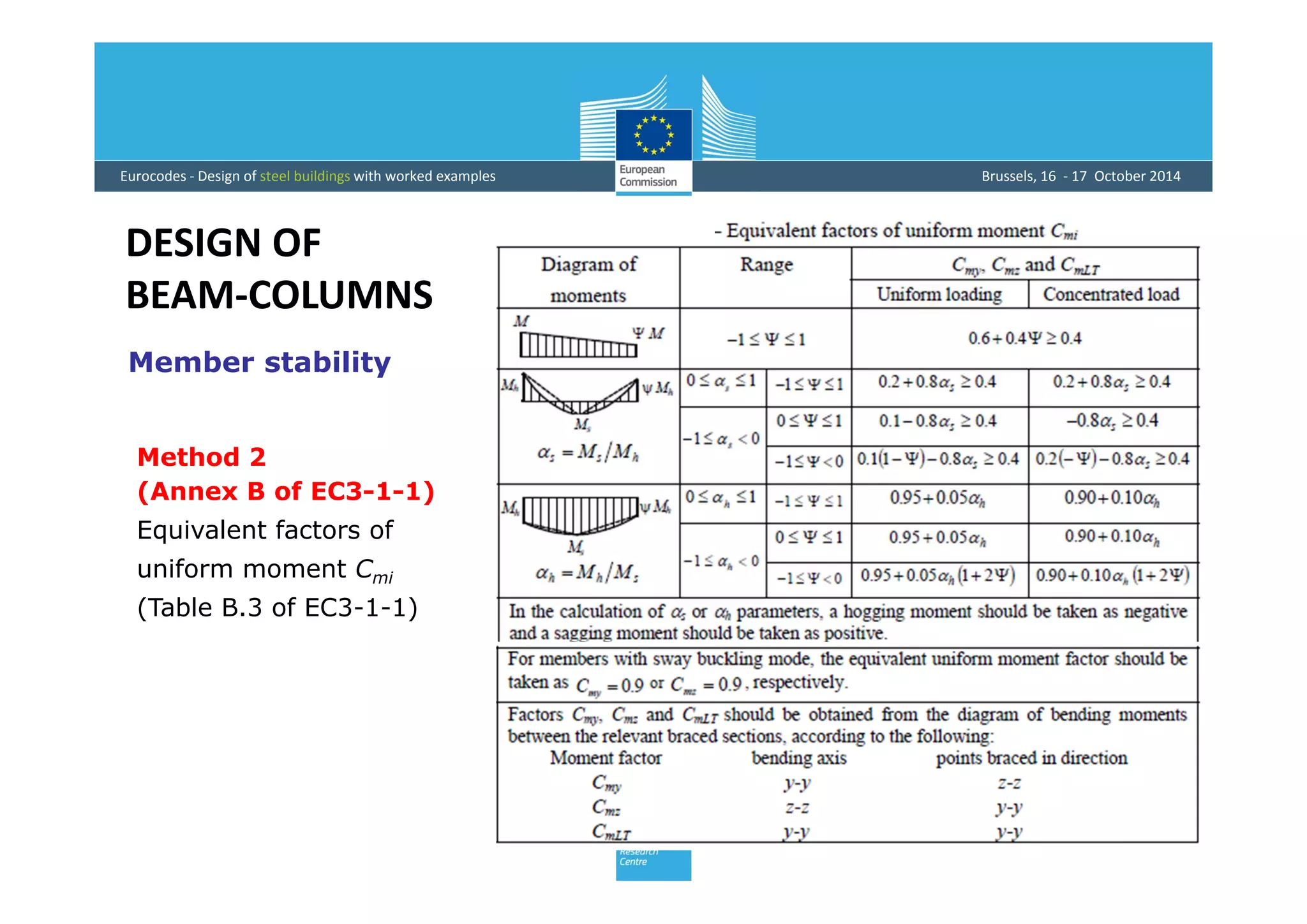
This document provides an overview of the design of steel structural members according to Eurocode standards, including columns, beams, and beam-columns. It discusses the main internal forces on members, the classification of cross-sections, and the approaches to checking the resistance of cross-sections and buckling resistance of members. It also provides an example calculation for the design of a steel column member under axial compression.