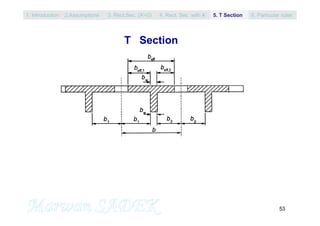
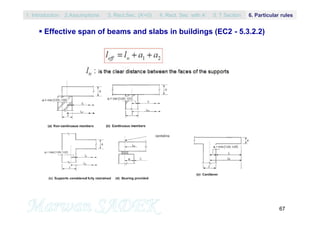
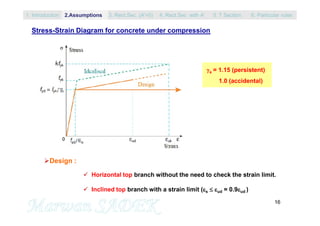
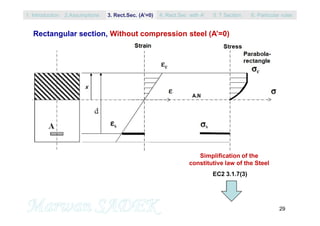
The document outlines the fundamentals of reinforced concrete structures, covering topics such as design assumptions, mechanical characteristics, durability, and various limit states for beams under simple bending. It references the evolution of standards and incorporates multiple sources, including the Eurocodes and previous French codes. Key elements discussed include stress-strain relationships, section analysis, and design considerations applicable to structural engineering practices.

1. 1
Reinforced Concrete
Structures 1 - Eurocodes
RCS 1
Professor Marwan SADEK
https://www.researchgate.net/profile/Marwan_Sadek
https://fr.slideshare.net/marwansadek00
Email : marwansadek00@gmail.com
If you detect any mistakes, please let me know at : marwansadek00@gmail.com

2. 2
RCS1
M. SADEK
Ch 1 : Generalities – Reinforced concrete in practice
Ch 2 : Evolution of the standards – Limit states
Ch 3 : Mechanical Characteristics of materials – Constitutive
relations
Ch 4 : Durability and Cover
Ch 5 : Beam under simple bending – Ultimate limit state ULS
Ch 6 : Beam under simple bending – serviceability limit state SLS
Ch 7 : Section subjected to pure tension

3. 3
Selected References
French BAEL Code (91, 99)
 Règles BAEL 91 modifiées 99, Règles techniques de conception et de calcul des
ouvrages et constructions en béton armé, Eyrolles, 2000.
 J. Perchat (2000), Maîtrise du BAEL 91 et des DTU associés, Eyrolles, 2000.
 J.P. Mougin (2000), BAEL 91 modifié 99 et DTU associés, Eyrolles, 2000.
 ….
EUROCODES
 H. Thonier (2013), Le projet de béton armé, 7ème édition, SEBTP, 2013.
 Jean-Armand Calgaro, Paolo Formichi ( 2013) Calcul des actions sur les
bâtiments selon l'Eurocode 1 , Le moniteur, 2013.
 J. M. Paillé (2009), Calcul des structures en béton, Eyrolles- AFNOR, 2009.
 Jean Perchat (2013), Traité de béton armé Selon l'Eurocode 2, Le moniteur,
2013 (2ème édition)
 Manual for the design of concrete building structures to Eurocode 2, The
Institution of Structural Engineers, BCA, 2006.
 A. J. Bond (2006), How to Design Concrete Structures using Eurocode 2, The
concrete centre, BCA, 2006.
https://usingeurocodes.com/
M. SADEK

4. 4
In addition to Eurocodes, the references that are mainly
used to prepare this course material are :
 Thonier 2013
 Perchat 2013
 Paillé 2009
Some figures and formulas are taken from
 Cours de S. Multon - BETON ARME Eurocode 2 (available on internet)
 Cours béton armé de Christian Albouy
M. SADEK

5. 5
Chapter V
Beam under simple bending – Ultimate limit
state ULS
1. Introduction
2. Design Assumptions
3. Rectangular Section without compression Steel
4. Rectangular Section with compression Steel
5. T Section
6. Particular rules

6. 6
M. SADEK
 Embedded beam
 Drop Beam
 Inverted beam
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

7. 7
M. SADEK
 Beam subjected to simple bending : M(x), V(x)
Note : In Reinforced concrete, bending stress and shear stress are treated separately.
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

8. 8
M. SADEK
Simple / Pure bending
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

9. 9
 Initiation of cracking
 Increase in Cracks
 Excessive strain in Steel / Crushing of Concrete
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

10. 10
M. SADEK
 Beam subjected to simple bending (ULS)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

11. 11
ASSUMPTIONS
H1) Principle of Navier-Bernoulli : After deformation, plane sections
remain plane and normal to the axis of the beam (linear strain diagram)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

12. 12
ASSUMPTIONS
H2) The tensile strength of the concrete is neglected
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

13. 13
ASSUMPTIONS
H3) bundled bars are treated as a single bar of a diameter derived
from the equivalent total area and placed at the COG of the group
H4) Total bond between concrete and steel (no relative slip)
at the contact : s=c
H5) The design stress-strain diagram for the concrete and the steel
are :
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

14. 14
Stress-Strain Diagram for concrete under compression
a) Parabola-rectangle
b) Bi-linear
fcd :Design value of concrete compressive strength (cylinder, t28 days)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

15. 15
c) Rectangular stress distribution
 Note : In the present course, we will use the diagram c (simplified).
The use of diagrams a and b are authorized by the EC2, See Annexes
for more details
cc= 1 (FNA)
C = 1.5 (Persistent situation ) ; 1.2 (Accidental situation)
Stress-Strain Diagram for concrete under compression
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

16. 16
Design :
 Horizontal top branch without the need to check the strain limit.
 Inclined top branch with a strain limit (s  ud = 0.9ud )
s = 1.15 (persistent)
1.0 (accidental)
Stress-Strain Diagram for concrete under compression
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

17. 17
Example : Persistent situation : fyd = fyk / s= 435 MPa
se = fyd/Es = 2.17.10-3
 < se => s = 200 000 
 > se => s = 435 MPa.
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

18. 18
 s > se (persistent situation)
s  435 + 727 (s -2.17.10-3) < 466 MPa for steel B
s  435 + 952 ( s -2.17.10-3) < 454 MPa for steel A
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

19. 19
Rule of 3 Pivots :
The design of a RC section at ULS is carried out assuming that the stress-strain
diagram through one of the 3 Pivots A, B or C.
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

20. 20
 Pivot A (Not very frequent)
 Steel : c  cu
s = ud that depends on the steel type (A, B or C)
(no limitation when the horizontal top branch diagram is used)
Difference with BAEL : The EC2 fix the pivot A at ud higher than 10x10-3 (BAEL)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

21. 21
 Pivot B (Common Case)
 Concrete : c = cu2 =3.5 ‰ , c2 =2 ‰ (for fck50 MPa)
s  ud
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

22. 22
Pivot C
(h-y) / h = c2/cu2 => y = (1-c2/cu2).h
(Compression, bending with axial force)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

23. 23
Simple Bending, ULS
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

24. 24
 Fundamental Combination (detail in Ch. 2)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

25. 25
c
s
sc
Strain
Diagram
Internal
Forces
Fc,sc
Fsc
Fc
Fs
z
 A : Cross sectional area of reinforcement (tension zone) (A or As)
 d : Effective depth of a cross-section : distance from the C.O.G of the tension steel to the extreme
compression fibre
A’ : Cross sectional area of compression steel
 d’ : distance from the C.O.G of the compression steel A’ to the extreme compression fibre
 z : Lever arm of internal forces
M > 0
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

26. 26
 Fc : Resultant of compression force in the concrete
 Fsc : Resultant of compression force in the compression steel
 Fc,sc : Resultant of Fc and Fsc
 Fs : Resultant of tensile force at the tensile steel
 x : Position of the N.A
c
s
sc
Strain
Diagram
Internal
Forces
x Fc,sc
Fsc
Fc
Fs
z
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

27. 27
c
s
sc
x Fc,sc
Fsc
Fc
Fs
z
 Equilibrium of forces Fs = Fc,sc
 Equilibrium of moments MEd = Fc,sc .z = Fs.z
 3 Unknowns (in general) : A, A’, x
Strain
Diagram
Internal
Forces
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

28. 28
Rectangular section, Without compression steel (A’=0)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

29. 29
Simplification of the
constitutive law of the Steel
EC2 3.1.7(3)
Rectangular section, Without compression steel (A’=0)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

30. 30
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

31. 31
Fc
FS
Fc = Fs
MED = Fc.z
z
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

32. 32
 Dimensionless Form :
By substituting :
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

33. 33
 fck 50 MPa,  = 1 ; =0.8
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

34. 34
Note that :
x = u.d =(c / c+s) d
u = (c / c+s)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

35. 35
 Boundaries of Pivots A, B
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

36. 36
 Steel type A  ud = 22,5 .10-3  AB = (3.5 / 3.5+22.5) = 0.135  AB = 0.102
 Steel type B   AB =0.072  AB = 0.056
 Steel type C   AB =0.049  AB = 0.039
 fck  50 MPa,  = 1 ; =0.8
 Boundaries of Pivots A, B
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

37. 37
 Pivot B AB  u
It can be noted that in general, the Pivot B is reached
 c = cu2 =3.5 ‰ ; s  ud
 s = (1/u -1) cu
(The concrete reaches its maximum strength)
 Boundaries of Pivots A, B
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

38. 38
 Pivot B AB  u  lim
 The tensile steel stress should not be in the elastic domain (non economical
solution) ! In this case, the tensile steel section should be reduced , or a
compression steel should be added.
s  ud but s  se
Line BE (Pivot B & steel at
elastic limit)
 Boundaries of Pivots A, B
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

39. 39
(fck  50 Mpa)
Persistant Situation Accidental Situation
s = 1.15 s = 1
fyk(MPa) lim lim lim lim
400 0.668 0.392 0.636 0.380
500 0.617 0.372 0.583 0.358
lim = BE
 Pivot B AB  u  lim
 Boundaries of Pivots A, B
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

40. 40
 Pivot A
s =ud ; c =cu
u  AB
 Boundaries of Pivots A, B
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

41. 41
 Tensile steel section A (fck 50 MPa)
a) Stress-Strain diagram with Inclined Top branch
i. u  AB  Pivot A
s = 455 MPa (Steel A) , 466 MPa (Steel B)
ii. AB  u  lim  Pivot B
s = (1/u -1) cu
s  435 + 727 (s -2.17.10-3) < 466 MPa Steel B
s  435 + 952 (s -2.17.10-3) < 454 MPa Steel A
(A’=0, u  lim )
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

42. 42
 Tensile steel sectiopn A (fck 50 MPa)
b) Stress-Strain diagram with horizontal Top branch
(A’=0, u  lim )
s = fyd
Note : No limitation for the steel strain
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

43. 43
Note 1
 Effective depth d – Initial value dini
 The exact value of d could not be determined before the choice of the steel
reinforcement.
 Take d  0.9 h for common beams (this formula is not safe for embedded beam
and for slab with low thickness  20 cm)
Take d = h – cnom – 1 cm (Slab with a thickness  20 cm )
After the determination of the reinforcement, it becomes possible to calculate the
exact value of d=dreal. If dreal < dini , the steel reinforcement section As should be
recalculated.
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

44. 44
 Note 2
 Approximate value of A (Quick check)
z  0.9d ; d  0.9 h
 This formula doesn't give any information about the compression stress
in the concrete. It becomes obsolete if a compression steel is required.
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

45. 45
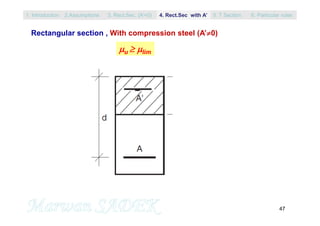
 Minimum Reinforcement (to prevent brittle failure)
 For rectangular section bh, the ultimate resistant bending moment of Non-
reinforced concrete :
MRc = (I/v)  fctm = (b.h²/6)  fctm
 The minimum As,min section should resist the following moment
MRs = As,min  fyk  z
 By considering MRc = MRs , and substituting z  0.9 d ; h d / 0.9
As,min = b.d.[fctm/(0.9  0.81  6)fyk]  0.23 b d fctm / fyk
 L’EC2 replace the value of 0.23 by 0.26 and fix a lower limit of the quantity 0.26 fctm/fyk
with the value 0.0013
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

46. 46
 Minimum Reinforcement
 Maximum Reinforcement
As,max = 0,04 Ac
 Ac : denotes for the cross sectional area of the concrete
 As,max : Maximum steel reinforcement in both compression and
tension zones
 As,min : Minimum tensile section of longitudinal steel reinforcement;
bt : denotes the mean width of the tension zone;
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

47. 47
Rectangular section , With compression steel (A’0)
u  lim
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

48. 48
 3 unknowns (A, A’, x) / 2 equations ???
 Infinite number of solutions
 Possibility n°1 : Minimum of “A+ A’ " (long run)
 Possibility n°2 : Concept of limit Moment (adopted in general)
- Resolution by the decomposition method - 2 imaginary sections
u  lim
Rectangular section , With compression steel (A’0)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

49. 49
2 imaginary sections
 Maximum capacity of the concrete Mlim  A1
 The compression steel A’ will resist (Med  Mlim)  A2
u  lim  Med  Mlim= lim .b.d².fcd
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

50. 50
cu
s
sc
x=lim.d
d’
d
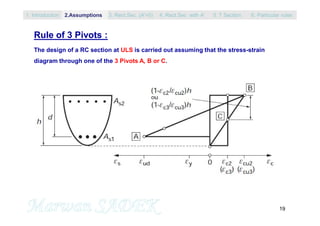
A1 = Mlim / (1 – 0.4.lim).d.fyd
A’ = (Med – Mlim) / [sc . (d-d’)]
sc = 3,5.10-3. (1-d’/xlim)
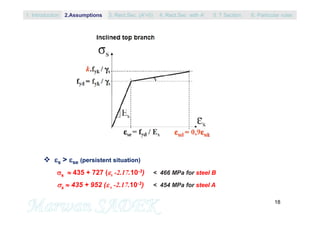
 The value of sc is close to 3 °/°° (>se), in other terms sc=fyd when using the diagram
with horizontal top branch, and a value slightly great than fyd when using the diagram
with inclined top branch.
 In general, we take a value sc=fyd .
A2 = A’. sc / s = A’. fyd / s
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

51. 51
A1 = Mlim / [(1 – 0.4.lim).d.fyd]
A2 = A’. sc / s
A’ = (Med – Mlim) / [fyd . (d-d’)]
 When using same types and grade for A and A’  sc = s = fyd
 A2 = A’
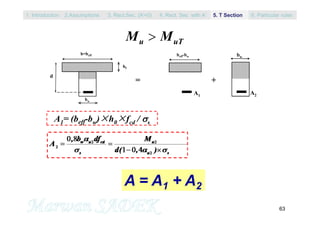
A = A1 + A2
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

52. 52
 Note 1 : The EC2 don’t restrict the moment that could be supported by
the compression steel like the previous BAEL standard (40% Med).
However A’ is limited by the maximum requirement
A+A’  As,max = 0,04 Ac
 Note 2 : Any compression longitudinal reinforcement (diameter )
which is included in the resistance calculation should be held by
transverse reinforcement with spacing not greater than 15 .
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect.Sec with A’ 6. Particular rules

53. 53
T Section
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

54. 54
 Effective width of flanges (all limit states)
 l0 : distance between points of zero moment
(EC 2-1-1, 5.3.2)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

55. 55
 Effective width of flanges (All limit states)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

56. 56
(EC 2-1-1, 5.3.2) Effective width of flanges (All limit states)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

57. 57
 Maximum resistant moment that could be supported by the
flange (flange in compression)
2
f
uT eff f cd
h
M b h f (d ) 
1sA
ux fh
s 1sN
1cN
 ff h,dz 501
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

58. 58
Case 1: Common case M Mu uT
bw
b = beff
d
hf
The Neutral Axis is located in the flange, the
flange is partially in compression
The T section is calculated as a rectangular
section (width beff and height h)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

59. 59
Case 2: The Neutral Axis is located in the WebM Mu uT
Divide the section in 2 imaginary sections
 The reinforcement section is expected to be very significant
bw
b=beff
d
hf
=
beff-bw
A1
A2
bw
+
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

60. 60
M Mu uT
1
eff w
u uT
eff
b b
M M
b

 Section A1 will resist:
bw
b=beff
d
hf
=
beff-bw
A1
A2
bw
+
A1= (beff-bw)×h0×fcd / s
(s = fyd, diagram with
horizontal top branch)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

61. 61
M Mu uT
 Section A2 will resist
 Calculation identical to a rectangular section with a width
bw and a height h
bw
b=beff
d
hf
=
beff-bw
A1
A2
bw
+
M M Mu u u2 1 
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

62. 62
M Mu uT
 s = fyd , diagram with horizontal top branch or Pivot A (palier incliné)
 s = to be determined function of s if Pivot B (diagram with inclined top
branch). This stress could be used when calculating A1
cdw
u
u
fdb
M
2
2
2   u u2 2125 1 1 2  , ( )
 Note: Introduce A’ whenu2 > lim
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

63. 63
M Mu uT
bw
b=beff
d
hf
=
beff-bw
A1
A2
bw
+
A = A1 + A2
A1= (beff-bw)×h0×fcd / s
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

64. 64
Predimensioning of concrete section – Rectangular section
b
h
If b is not imposed , we can take
0.3 h  b  0.5 h
We fix b, and we find the value of h
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

65. 65
b
h
b/h  0.4 ; h  2.5 b
d  0.9 h = 2.25 d
 Pivot B AB  u  lim
Steel B 0.056  u  0.372
0.056  Med / bd²fcd  0.372
Predimensioning – Rectangular section
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

66. 66
b
h
Other criterion
- Design at SLS + maximum deflection condition
Steel A
Predimensioning – Rectangular section
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

67. 67
 Effective span of beams and slabs in buildings (EC2 - 5.3.2.2)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

68. 68
Other detailing arrangements (EC2 - 9.2.1.2)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

69. 69
 Source :Thonier (2013)
1. Introduction 3. Rect.Sec. (A’=0) 5. T Section2.Assumptions 4. Rect. Sec with A’ 6. Particular rules

70. 70
Exercices
 Rectangular section without compression steel:
 Tensile steel reinforcement
o using the stress strain diagram with inclined top branch
o using the stress strain diagram with horizontal top branch
o Exact value of d
 Rectangular section with compression steel:
 Determination of the reinforcement steel sections (tension and
compression)
 Predimensioning of a rectangular section of concrete and determination of
the steel reinforcement while taking in account the beam self weight
 Design of T section