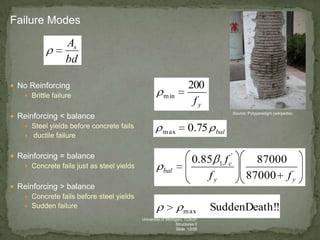
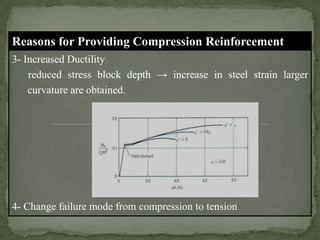
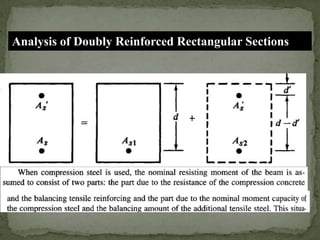
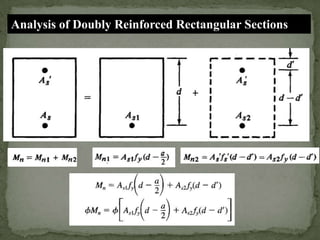
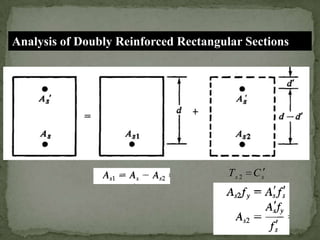
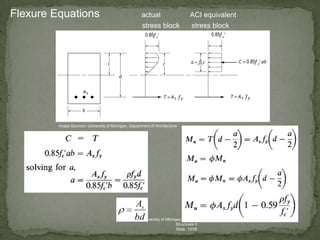
The document discusses the design and analysis of pre-stressed concrete structures, focusing on the ultimate strength concepts for singly and doubly reinforced sections. It outlines the methods for calculating design loads, analyzing internal moments, and determining steel reinforcement requirements based on varying conditions and codes. Important considerations include the stress-strain relationships, failure modes, and specific analytical procedures for rectangular beam designs.

1. PRE-STRESSED CONCRETE LAB
CE-416
Name: Sadia Mahajabin
ID: 10.01.03.098
Section: B
Course Teacher:
Mr. Galib Muktadir & Sabreena N. Mouri
Department of Civil Engineering

2. (SINGLY & DOUBLY)

3.  Based on the ultimate strength of the structure
assuming a failure condition either due to concrete
crushing or by yielding of steel.Additional strength of
steel due to strain hardening is not encountered in the
analysis or design.
 Actual / working loads are multiplied by load factor to
obtain the design loads.
 ACI codes emphasizes this method.

4. Being used since 1957.

5. 1. Plane sections before bending remain plane after bending.
2. Strain in concrete is the same as in reinforcing bars at the
same level, provided that the bond between the steel and
concrete is sufficient to keep them acting together under the
different load stages i.e., no slip can occur between the two
materials.
3. The stress-strain curves for the steel and concrete are known.
4.The tensile strength of concrete may be neglected.
5.At ultimate strength, the maximum strain at the extreme
compression fiber is assumed equal to 0.003

7. DESIGN AND ANALYSIS
The main task of a structural engineer is the analysis and design of
structures. The two approaches of design and analysis will be used
Design of a section:
This implies that the external ultimate moment is known, and it is
required to compute the dimensions of an adequate concrete section
and the amount of steel reinforcement. Concrete strength and yield of
steel used are given.
Analysis of a section:
This implies that the dimensions and steel used in the section (in
addition to concrete and steel yield strengths) are given, and it is
required to calculate the internal ultimate moment capacity of the
section so that it can be compared with the applied external ultimate
moment.

8. ▫
▫
Singly reinforced section
Doubly reinforced section

10. Flexure Equations
actual
ACI equivalent
stress block
stress block
Image Sources: University of Michigan, Department of Architecture
As
bd
University of Michigan, TCAUP
Structures II
Slide 10/26

11. Relationship b / n the depth `a’ of the equivalent rectangular stress
block & depth `c’ of the N.A. is
a = β1 c
β1= 0.85
; fc’ 4000 psi
β1= 0.85 - 0.05(fc’ – 4000) / 1000
; 4000 < fc’ 8000
β1= 0.65
; fc’> 8000 psi
b
= Asb / bd
= 0.85fc’ ab / (fy. d)
= β1 ( 0.85 fc’ / fy) [ 87,000 / (87,000+fy)]

12. Failure Modes
As
bd
 No Reinforcing
 Brittle failure
 Reinforcing < balance
 Steel yields before concrete fails
 ductile failure
 Reinforcing = balance
 Concrete fails just as steel yields
 Reinforcing > balance
 Concrete fails before steel yields
 Sudden failure
m in
200
fy
Source: Polyparadigm (wikipedia)
m ax
bal
0.75
bal
0.85 1 f c'
fy
m ax
University of Michigan, TCAUP
Structures II
Slide 12/26
87000
87000 f y
SuddenDeat h!!

13. Rectangular Beam Analysis
Data:



Section dimensions – b, h, d, (span)
Steel area - As
Material properties – f’c, fy
Required:
Strength (of beam) Moment - Mn
Required (by load) Moment – Mu
Load capacity
Steps:



1. Find
As f y
a
0.85 f c'b
or
f yd
0.85 f c'
= As/bd
(check
min<
<
max)
2. Find a
Mn
M
u
A f d
M s y
n
a
2
3. Find Mn
4. Calculate Mu<=
Mn
5. Determine max. loading (or span)
Image Sources: University of Michigan, Department of Architecture
University of Michigan, TCAUP
Structures II
Slide 13/26
(1.4 wDL 1.7 wLL )l 2
Mu
8
Mu8
1.7 wLL
1.4 wDL
2
l

14. Rectangular Beam Analysis
Data:
 dimensions – b, h, d, (span)
 Steel area - As
 Material properties – f’c, fy
Required:
 Required Moment – Mu
1. Find
= As/bd
(check min<
<
max)
University of Michigan, TCAUP
Structures II
Slide 14/26

15. Rectangular Beam Analysis
2.
Find a
3.
Find Mn
4.
cont.
Find Mu
University of Michigan, TCAUP
Structures II
Slide 15/26

16. Rectangular Beam Design
Data:



Mu
Load and Span
Material properties – f’c, fy
All section dimensions – b and h
(1.4wDL 1.7 wLL )l 2
8
Required:
Steel area - As
Steps:
1.
Calculate the dead load and find Mu
2.
d = h – cover – stirrup – db/2 (one layer)
3.
Estimate moment arm jd (or z) 0.9 d
and find As
4.
Use As to find a
5.
Use a to find As (repeat…)

6.
Choose bars for As and check
7.
As
fy d
a
max & min
Check Mu< Mn (final condition)
Mn
University of Michigan, TCAUP
Structures II
Slide 16/26
Mu
a
2
As f y
0.85 f c'b
As f y d
a
2

17. Rectangular Beam Design
Data:

Load and Span
Material properties – f’c, fy
Mu
Required:
Steel area - As
Beam dimensions – b or d
Steps:
1.
Choose (e.g. 0.5 max or 0.18f’c/fy)
2.
Estimate the dead load and find Mu
3.
Calculate bd2
4.
Choose b and solve for d


bd
2
(1.4wDL 1.7 wLL )l 2
8
Mu
f y 1 0.59
b is based on form size – try several to find best
5.
6.
7.
Estimate h and correct weight and Mu
Find As= bd
Choose bars for As and determine spacing and
cover. Recheck h and weight.
University of Michigan, TCAUP
Structures II
Slide 17/26
As
bd
fy / f c'

18. Rectangular Beam Design
Data:
Load and Span
Material properties – f’c, fy
Required:

Steel area - As

Beam dimensions – b and d


1.
2.
Estimate the dead load and find Mu
Choose (e.g. 0.5 max or 0.18f’c/fy)
University of Michigan, TCAUP
Structures II
Slide 18/26

19. Rectangular Beam Design cont
3.
Calculate bd2
4.
Choose b and solve for d
b is based on form size.
try several to find best
University of Michigan, TCAUP
Structures II
Slide 19/26

20. Rectangular Beam Design
5.
6.
7.
Estimate h and correct
weight and Mu
Find As= bd
Choose bars for As and
determine spacing and
cover. Recheck h and
weight.
University of Michigan, TCAUP
Source: Jack C McCormac, 1978 Design of Reinforced Concrete, Harper and Row, 1978
Structures II
Slide 20/26

21. Doubly Reinforced Rectangular Sections
Beams having steel reinforcement on both the tension and
compression sides are called doubly reinforced sections.
Doubly reinforced sections are useful in case of limited
cross sectional dimensions being unable to provide the
required bending strength even when the maximum
reinforcement ratio is used

22. 1- Reduced sustained load deflections.
• transfer load to compression steel
• reduced stress in concrete
2- Ease of fabrication
• use corner bars to hold & anchor stirrups

23. Reasons for Providing Compression Reinforcement
3- Increased Ductility
reduced stress block depth → increase in steel strain larger
curvature are obtained.
4- Change failure mode from compression to tension

24. Four Possible Modes of Failure
 Under reinforced Failure
 ( Case 1 ) Compression and tension steel yields
 ( Case 2 ) Only tension steel yields
 Over reinforced Failure
 ( Case 3 ) Only compression steel yields
 ( Case 4 ) No yielding Concrete crushes

25. Analysis of Doubly Reinforced Rectangular Sections

26. Analysis of Doubly Reinforced Rectangular Sections

27. Analysis of Doubly Reinforced Rectangular Sections
Ts 2
Cs

28. Analysis of Doubly Reinforced Rectangular Sections
s
fs
s
Es
Es
Es
T
As f y
As f y
Cc C s
0.85f c ab
0.85f c 1cb
As
As f s
c d
c
0.003E s
c d
0.003
c
c d
0.003E s
c
200, 000 MPa
29, 000 ksi
fy

29. Analysis of Doubly Reinforced Rectangular Sections
Procedure:
As f y
fs
s
0.85f c 1cb
s
Es
c d
c
As
c d
c
0.003E s
c d
0.003 0.005?
c
0.003E s
fy
find c