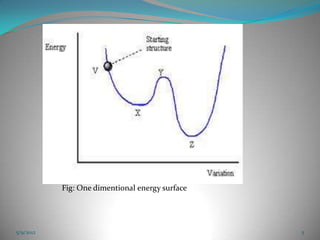
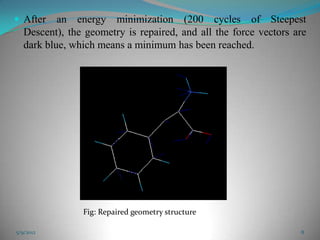
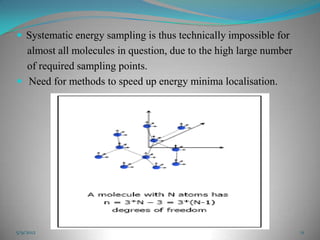
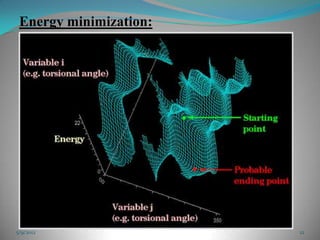
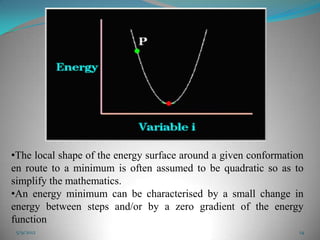
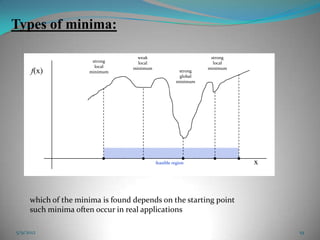
The document discusses energy minimization methods in computational chemistry. It explains that energy minimization aims to find the lowest energy confirmation of a molecule by varying its intramolecular degrees of freedom. This corresponds to stable molecular states. Several algorithms are used for energy minimization, including steepest descent, conjugate gradient, and Newton-Raphson methods. The goal is to locate minima on the multidimensional energy surface in the fewest computational steps.

1. Presented by Guided by
Mr. Pradeep V. Kore Mr.
M. Pharm. ( II Sem ) M. Pharm.
Department of Pharmaceutical Chemistry
JSPM’s Charak College of Pharmacy & Research,
Gat No. 720(1/2), Wagholi, Pune-Nagar road,
Wagholi-412 207.
1 1

2. CONTENTS:
5/9/2012 2

3. INTRODUCTION
 In computational chemistry energy minimization (also called
energy optimization or geometry optimization) methods are
used to compute the equilibrium configuration of molecules
and solids.
 Energy minimizatiom methods can precisely locate minimum
energy confirmation by mathematically “homing in” on the
energy function minima (one at a time).
 The goal of energy minimization is to find a route (consisting
of variation of the intramolecular degrees of freedom) from an
initial confirmation to nearest minimum energy confirmation
using the smallest number of calculations possible.
5/9/2012 3

4.  In molecular modeling we are interested in minimum points on
the energy surface.
 Minimum energy arrangments of the atoms corresponds to
stable states of the system:
 Any movement away from a minimum gives a configuration
with higher energy.
 There may be a very large number of minima on energy
surface. The minimum with very lowest energy is known as the
Global Energy Minimum.
5/9/2012 4

5. Fig: One dimentional energy surface
5/9/2012 5

6. What can energy minimization do?
 It can repair distorted geometries by moving atoms to release
internal constraints, as shown below:
 In this example, the CZ of a phenylanalnine ring was artificially
stretched out, which lead to bonds much too long.
Fig: Phenylanalnine
5/9/2012 6

7.  By first invoking an energy computation, the C-terminal Oxygen
(OXT) is added to the residue. Note that the residue must also be
protonated, and in this case an N-terminal blocking group (HHT)
is added. Then the energy computation can be done:
The direction in which atoms should be displaced in order to
reach a lowe energy state are shown by dotted lines. A
minimal deplacement appears in dark blue, while a big
deplacement appear in red (blue-green-red gradient).
5/9/2012 7

8.  After an energy minimization (200 cycles of Steepest
Descent), the geometry is repaired, and all the force vectors are
dark blue, which means a minimum has been reached.
Fig: Repaired geometry structure
5/9/2012 8

9. Energy minimising procedures
1) Conformational energy searching
2) Energy minimisation
3) Minimisation algorithms
5/9/2012 9

10. Conformational energy searching
 Energy is a function of the degrees of freedom in a molecule:
bonds, angles, dihedrals.
 Conformational energy searching is used to find all of the
energetically preferred conformations of a molecule.
 This is mathematically equivalent to locating all of the minima of
the energy function of the molecule.
 The possible conformations for a molecule lie on an n-dim.
Lattice, with n being the number of degrees of freedom.
5/9/2012 10

11.  Systematic energy sampling is thus technically impossible for
almost all molecules in question, due to the high large number
of required sampling points.
 Need for methods to speed up energy minima localisation.
5/9/2012 11

12. Energy minimization:
5/9/2012 12

13.  Minimisation algorithms are designed to head down-hill towards
the nearest minimum.
 Remote minima are not detected, because this would require some
period of up-hill movement.
 Minimisation algorithms monitor the energy surface along a series
of incremental steps to determine a down-hill direction.
5/9/2012 13

14. •The local shape of the energy surface around a given conformation
en route to a minimum is often assumed to be quadratic so as to
simplify the mathematics.
•An energy minimum can be characterised by a small change in
energy between steps and/or by a zero gradient of the energy
function
5/9/2012 14

15. Approximation of the quadratic energy function
 Approximation of the quadratic energy function is given by
aTaylor series:
f(x)= f(P) – bx + 1/2Ax2
P- is the current point
x -an arbitrary point on the energy surface
b- is the gradient at
P, A- is the
Hessian matrix
(the second partial derivatives) at P. A and b can be viewed
as parameters that fit the idealised quadratic form to the actual
energy surface.
5/9/2012 15

16. Minimisation algorithms
Simplex algorithm
- Not a gradient minimization method.
- Used mainly for very crude, high energy starting structures.
Steepest descent minimiser
- Follows the gradient of the energy function (b) at each step.
This results in successive steps that are always mutually
perpendicular, which can lead to backtracking.
- Works best when the gradient is large (far from a minimum).
- Tends to have poor convergence because the gradient becomes
smaller as a minimum is approached.
5/9/2012 16

17. Conjugate gradient and Powell minimiser
 Remembers the gradients calculated from previous steps to help
reduce backtracking.
 Generally finds a minimum in fewer steps than Steepest
Descent.
 May encounter problems when the initial conformation is far
from a minimum.
5/9/2012 17

18. Newton-Raphson and BFGS minimiser
- Predicts the location of a minimum, and heads in that direction.
- Calculates (Newton-Raphson) or approximates (BFGS) the second
derivatives in A.
- Storage of the A term can require substantial amounts of
computer memory
- May find a minimum in fewer steps than the gradient-only
methods.
- May encounter serious problems when the initial conformation is
far from a minimum.
5/9/2012 18

19. Types of minima:
weak strong
strong local local
local minimum minimum
f(x) minimum strong
global
minimum
feasible region x
which of the minima is found depends on the starting point
such minima often occur in real applications
5/9/2012 19