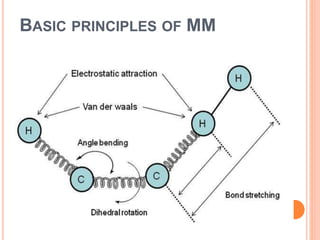
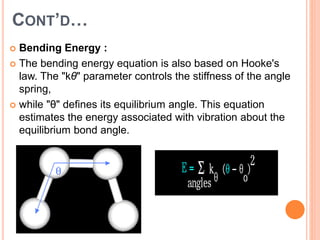
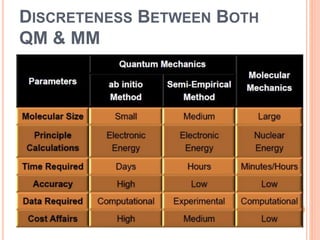
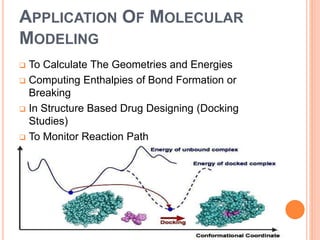
The document provides an overview of molecular mechanics as a computational method for studying molecular systems, focusing on potential energy surfaces and the calculations of various energy components including bonded and non-bonded interactions. It outlines fundamental principles of molecular mechanics, the role of force fields, and various applications in drug design and simulation. Additionally, it mentions novel techniques that combine quantum mechanics with molecular mechanics for enhanced accuracy in modeling complex systems.

1. MOLECULAR
MECHANICS
Presented By
Akshay Avinash Kank
(M.Pharm, First Year)
Guided By
Proff. Dr. S.R. Butle
(M.Pharm Ph.D)

2. PARAMETERS
 Introduction to computational chemistry
 Need to study
 Molecular mechanics
 Basic principle of MM
 Force field methods
 Novel Techniques
 Discreteness between QM and MM
 Application
 References

3. COMPUTATIONAL CHEMISTRY
 Computational chemistry is a branch of chemistry
that uses principles of computer science to assist in
solving chemical problems.
 Since chemistry concerns the study of properties of
substances or molecular systems in terms of
atoms, the basic challenge facing computational
chemistry is to describe or even predict-
1. The structure and stability of a molecular
system,
2. The (free) energy of different states of a
molecular systems,
3. Reaction processes within molecular systems.

4. MOLECULAR MECHANICS
 Molecular mechanics is a computational method
that computes the potential energy surface for a
particular arrangement of atoms using potential
functions that are derived using classical physics.
 Molecular mechanics ignores the electronic motions
and calculate the potential energy of a system as a
function of nuclear position only.
 Molecular mechanics methods are the basic for
other methods , such as construction of homology
models, molecular dynamics, crystallographic
structure refinement and docking.

5. CONT’D…
 The mechanical molecular models was developed out of
a need to describe molecular structures and properties
in as practical a manner as possible.
 Molecular mechanics methods are based on the
following principles:
 Nuclei and electrons are lumped into atom-like particles.
 Atom-like particles have a net charge.
 Interactions are based on springs and classical potentials.
 Interactions must be pre-assigned to specific sets of at
atoms.
 Interactions determine the spatial distribution of atom-
like particles and their energies.

6. BASIC PRINCIPLES OF MM

7. BASICS PRINCIPLES OF MM
 The basic functional form of an inter-atomic potential
encapsulates both bonded terms relating to atoms that are
linked by covalent bonds, and non-bonded. The specific
decomposition of the terms depends on the force field, but a
general form for the total energy in an additive force field can
be written as
E𝑡𝑜𝑡𝑎𝑙 = E bonded + E non-bonded
 where the components of the covalent and non-covalent
contributions are given by the following summations:
 E bonded =E bond +E angle + E dihedral
 E non-bonded =E electrostatic +E van der Waals

8. WHAT IS A FORCE FIELD?
 A force field is a mathematical function in which the
conformational energy of a system studied.
 Force fields are also sometimes referred to as potentials.
 Many different kinds of force fields have been developed over
the years.
 Some force-fields account for coupling between bending and
stretching in adjacent bonds in order to improve the accuracy
of the mechanical model.
 E = Es + Eb + Eω + Enb + …
Where:
E- The steric energy.
Es- Bond stretching
Eb- Bond angle bending
Eω- Torsional energy
Enb- Non bonded interactions.

9. CONT’D…
 Stretching Energy :
 The stretching energy equation is based on Hooke's law.
 The "kb" parameter controls the stiffness of the bond
spring, while "rO" defines its equilibrium length.
 Unique "kb" and "rO" parameters are assigned to each
pair of bonded atoms based on their types (e.g. C-C, C-
H, O-C, etc.).
 This equation estimates the energy associated with
vibration about the equilibrium bond length.

10. CONT’D…
 Bending Energy :
 The bending energy equation is also based on Hooke's
law. The "kθ" parameter controls the stiffness of the angle
spring,
 while "θ" defines its equilibrium angle. This equation
estimates the energy associated with vibration about the
equilibrium bond angle.

11. CONT’D…
 Torsional energy :
 Is primarily used to correct the
remaining energy terms, Represents
the amount of energy that must be
added to or subtracted from the
Energy terms to make the total
energy.
 Non-Bonded Energy :
 The non-bonded energy accounts for
repulsion, van der Waals attraction,
and electrostatic interactions.
 Van der Waals attraction occurs at
short range, interacting atoms move
apart by a few Angstroms.
 Repulsion occurs when the distance
between interacting atoms becomes
less than their contact radii

12. MOLECULAR MECHANICS MODELS
 AMBER:-
 Assisted model building with energy refinement (AMBER)
 It was parameterized specifically for proteins and nucleic acids
 CHARMM:-
 Chemistry at Harvard macromolecular mechanics (CHARMM).
 The academic version of this program is designated CHARMM
and the commercial version is called CHARMm
 It was originally devised for proteins and nucleic acids.
 GROMOS:-
 Groningen Molecular Simulation package
 COMPASS:-
 Condensed-phase Optimized Molecular Potentials for Atomistic
Simulation Studies
 MMFF:-
 Merck Molecular Force Field

13. NOVEL TECHNIQUE- IN
MOLECULAR MODELING
 QM/MM- Monte Carlo method
 This is the ‘Hybrid’ of quantum and molecular mechanics
 The QM/MM procedure is applicable when the system
can be partitioned into two regions;
 one region (the ‘active site’) requires an accurate QM
calculation of its potential and
 the second region (the rest of the system) acts as a
perturbation on the active site and can be treated with
an approximate and fast MM calculation of its potential.
 By using a quantum mechanical calculation, we can
treat bond breaking and bond-forming accurately at the
active site yet still take into account the role of the
surrounding atoms using MM.

14. DISCRETENESS BETWEEN BOTH
QM & MM

15. APPLICATION OF MOLECULAR
MODELING
 To Calculate The Geometries and Energies
 Computing Enthalpies of Bond Formation or
Breaking
 In Structure Based Drug Designing (Docking
Studies)
 To Monitor Reaction Path

16. REFERENCES
 Computer application in Pharmaceutical Research
and Development By Sean Ekins, A John Wiley and
Sons Publication.
 https://www.youtube.com/watch?v=GMsD8vPdL7o
 Practical application of computer aided drug design,
By Paul S. Charifson, Marcel Dekker INC.
 Chapter 3, molecular modeling techniques, By
Swami Ramanand Teerth Marathwada University.
 https://www.slideshare.net/RikeshlalShrestha/molecu
lar-modelling-75429338
 Molecular Modeling By Dr. Vibha Tandan, Shree
Publishers and Distributers, first Edition.