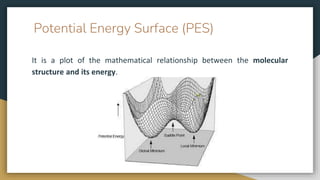
The document discusses molecular modeling and energy minimization methods, focusing on techniques to find the lowest energy conformation of a molecule, or geometry optimization. It outlines the basic steps of energy minimization, potential energy surfaces, different computational techniques, and specific methods such as steepest descent, Newton-Raphson, and conjugate gradient methods. The document provides a comprehensive overview of energy minimization processes and their applications in molecular mechanics.

1. MOLECULAR
MODELING
ENERGY MINIMIZATION METHODS
Prepared by:
Chandni Pathak
(180821101075)
8th Sem, B.Pharm
Parul Institute of Pharmacy

2. Contents
- Molecular Modeling
- Energy Minimization
- Basic Steps of EM
- EM techniques

3. MOLECULAR MODELING
Molecular Modeling is a group of computerized techniques which are
being used to predict molecular and biological properties or to analyze
molecular systems using the basic principles of theoretical chemistry in
conjunction with or without available experimental data.

4. ENERGY MINIMIZATION
The main objective of molecular mechanics is to find the lowest energy
conformation of a molecule and this process is termed as Energy minimization
or Geometry optimisation method.
Definition:-
It is the process of finding an arrangement in space of a collection of atoms
where, according to some computational model of chemical bonding, the net
interatomic force on each atom is acceptably close to zero and the position on
the Potential Energy Surface (PES) is a stationary point.

5. Potential Energy Surface (PES)
It is a plot of the mathematical relationship between the molecular
structure and its energy.

6. ENERGY MINIMIZATION
In short, it is a procedure that attempts to minimize the potential energy of the
system to the lowest possible point.
The system makes several changes in the atom position through rotation and
calculates energy in every position. This process is repeated many times to find
the position with lowest energy until an overall minimum energy is attained.
In every move the energy is kept lowered, otherwise the atom will return to its
original position.
The one full round of an atom rotation is called minimization step or iteration.

7. ENERGY MINIMIZATION
EM is used for :
1) Locating a stable conformation
2) Locating Global and Local minima
3) Locating a saddle point

8. 4 MAIN STEPS:
1. Computation of the potential energy of the starting geometry
2. Alterations of the atomic positions of each atom and computing the
energy of the entire molecule
3. If the energy of the new conformer is less than the starting one, adopt this
conformation and proceed for next alteration otherwise retain the first
one
4. Repeat the process till there is no more decrease in the potential energy

9. TECHNIQUES OF GEOMETRY OPTIMIZATION
A. Steepest descent
B. Newton-Raphson method
C. Conjugate gradient
D. Quasi-Newton Raphson or variable matrix method
E. Downhill Simplex

10. A. Steepest Descent Method
- Simplest method for Geometry
Optimization
- Also called as Gradient Descent
Method.
- Optimization algorithm for
obtaining local minimum of a multi-
dimensional function.
- The energy minimization
methodology needs to involve
identification of the point closest to
the starting structure.

11. A. Steepest Descent Method
Simplest technique which uses the first derivative (dE/dXi= 0).
Ri+1 = Ri - 𝞪Fi
Where, i = iteration number
Ri = Old coordinates
Ri+1 = New coordinates
Fi = Force (energy gradient) on the atoms at step ‘i’ and ‘𝛂’, a constant,
determining the extent to which force is applied

12. A. Steepest Descent Method
- This method converges rapidly when first derivatives are large, i.e.
the geometry is far away from the minimum.
- The method slows down considerably when it comes close to a
minimum.
- Near the minimum, its progress is so slow that it almost never
reaches the bottom.

13. B. Newton - Raphson minimization methods
- In this method, inverse of the second derivative matrix (Hessian) is
used.
- The method can be implemented in full or partial [Block diagonal
(BDNR)] matrix form.
- The method is the most computationally expensive per step of all the
methods utilized to perform EM.
- Advantage:- The minimization could converge in one or two steps.
- Disadvantage:- This method requires the calculation of the second
derivatives.

14. C. Conjugate Gradient Method
● It is a first order minimization technique.
● It uses for both the current gradient and the previous search direction
to drive the minimization.
● The number of computing cycles required for a conjugated gradient
calculation is approximately proportional to the number of atoms (N,
and the time per cycle is proportional to N2.
● Require fewer energy evaluations and gradient calculations
● Convergence characterizations are better than the steepest gradient.

15. D. Quasi - Newton Raphson Method
- These methods avoid the difficult evaluation of the generalized
inverse of the Hessian matrix.
- Consequently, these methods are faster ones.
- DFP (Davidson, Fletcher and Powell) and BFGS (Broyden, Fletcher,
Goldfard and Shanno) methods are representatives of this class.

16. F. Downhill Simplex Method
- It is a robust and non-derivative-based method which probably is one
of the easiest method to implement.
- It requires only function evaluation.

17. REFERENCE
1) https://www.slideshare.net/PavanBadgujar/seminar-energy-minimization-mettthod
2) https://vlab.amrita.edu/?sub=3&brch=277&sim=1491&cnt=1
3) A textbook of drug design and development by M.R. Yadav and P.R. Murumkar

18. THANK YOU