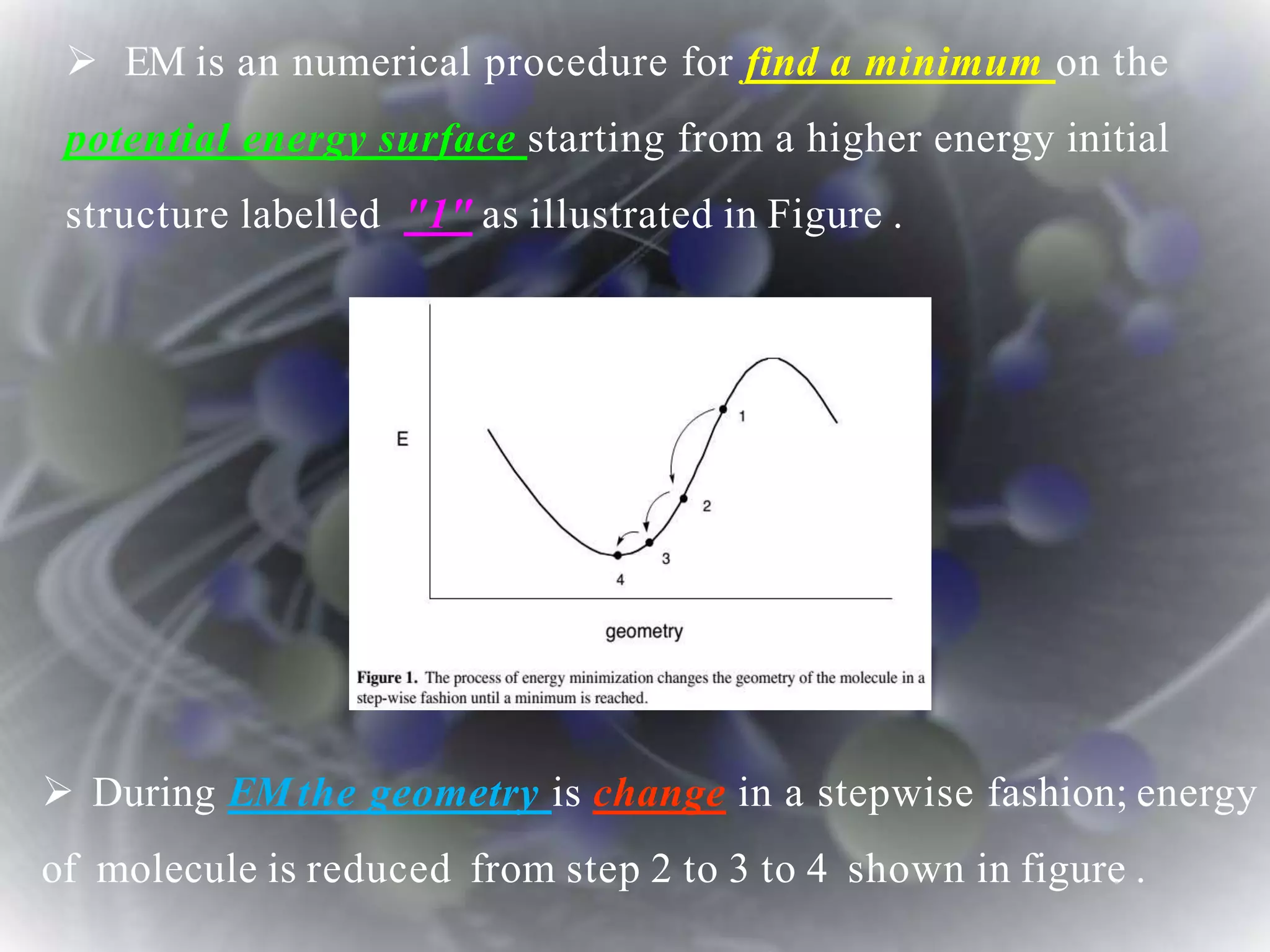
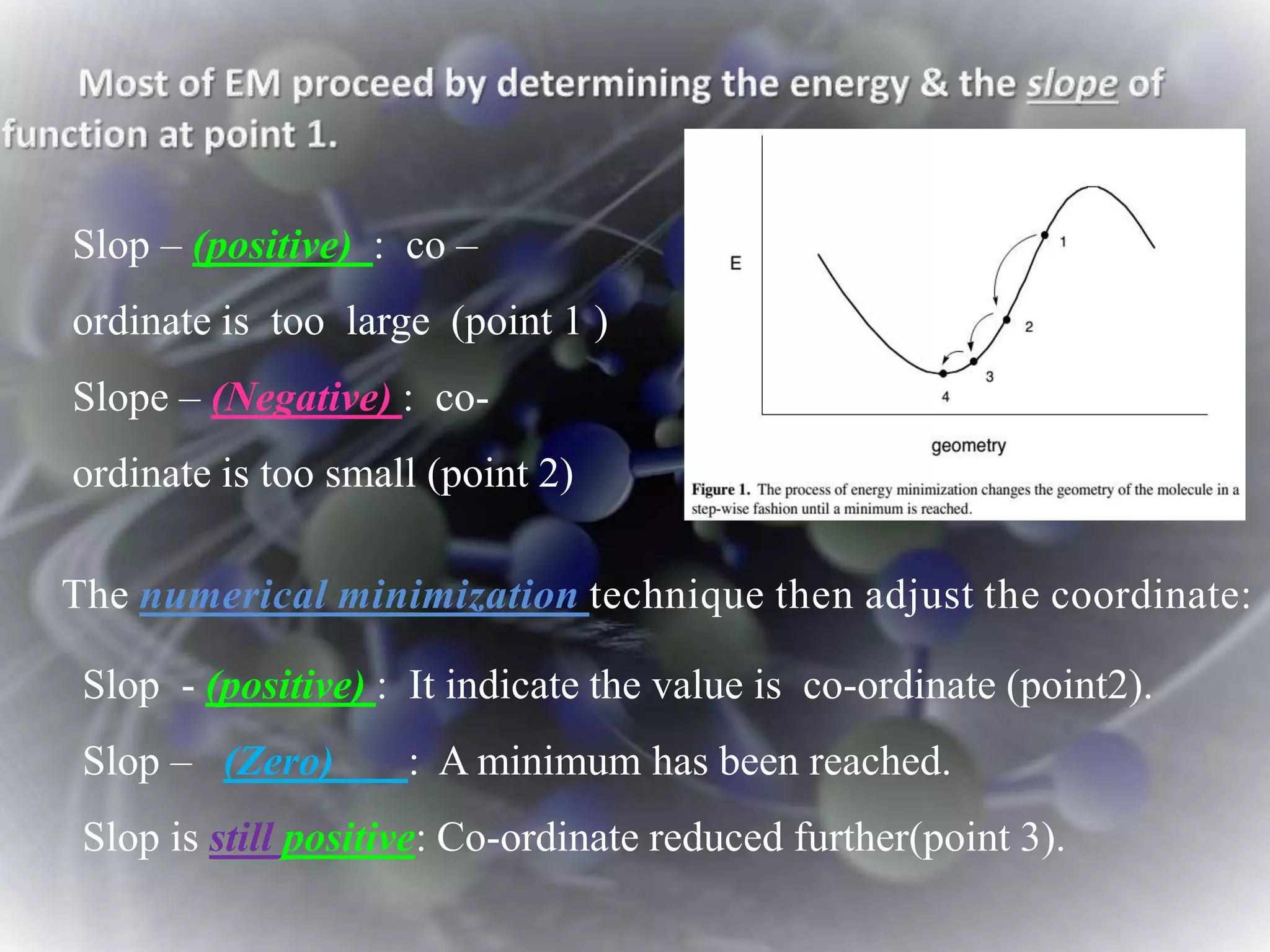
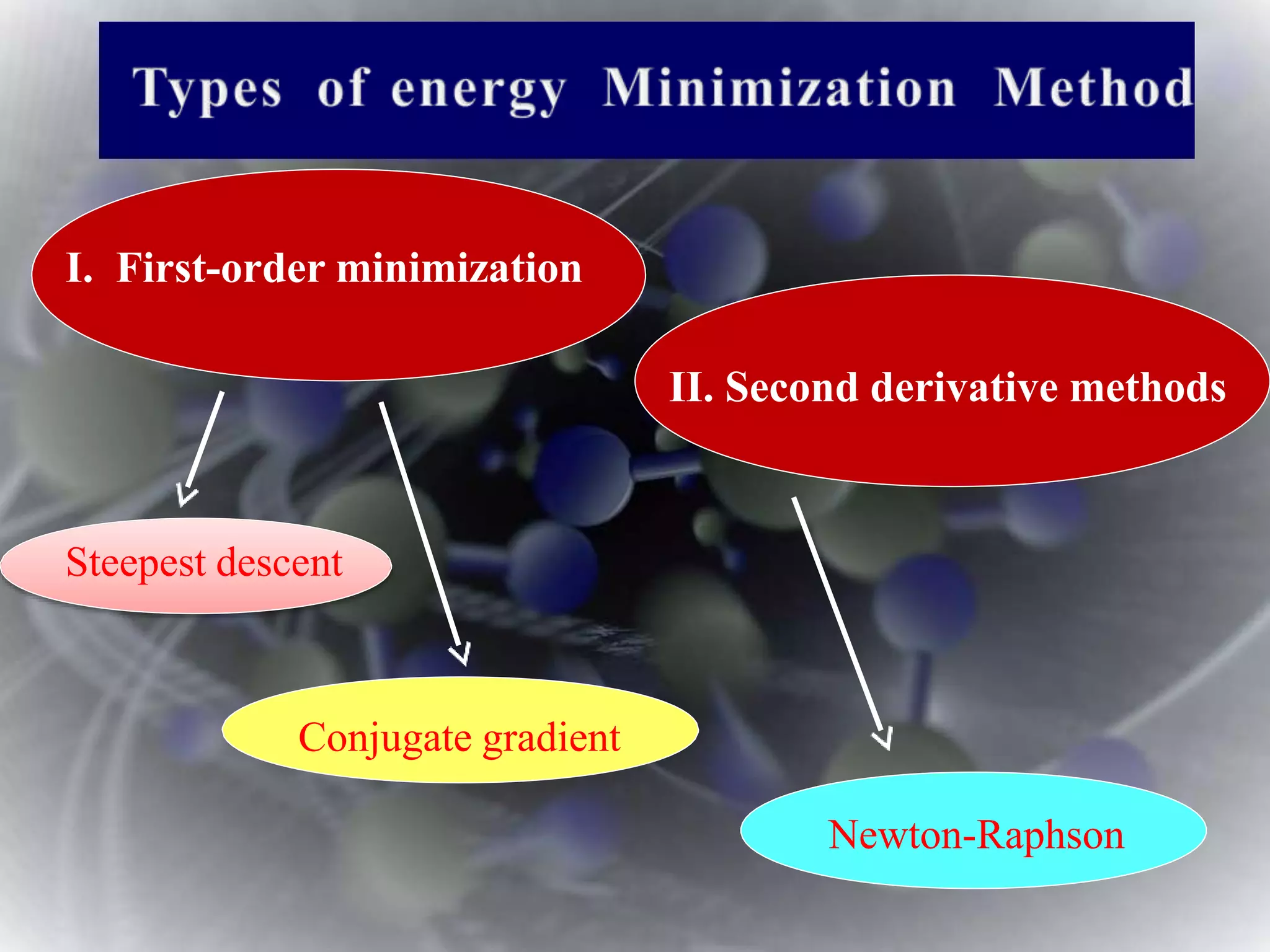
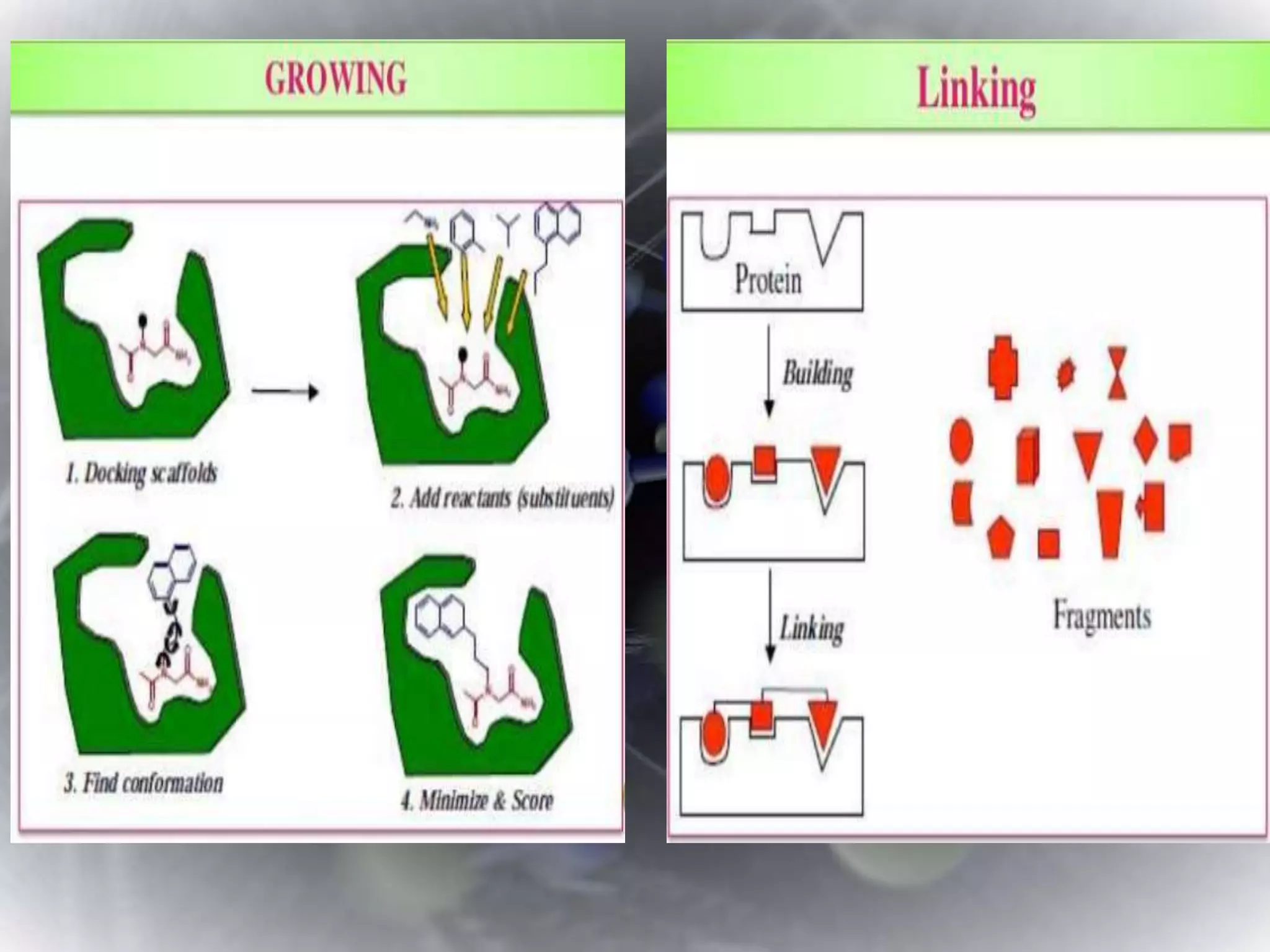
The document discusses various molecular modeling and computational chemistry techniques used to simulate molecular systems, including molecular dynamics, molecular mechanics, quantum mechanics methods, and molecular docking. It provides an overview of the different modeling strategies and computational tools used, such as determining receptor geometry from X-ray crystallography, energy minimization techniques, force field parameters, and quantum mechanical calculations. The goal of molecular modeling is to develop accurate models of molecular systems to predict properties and behavior without experimental testing.

1. EneEnerrggyyMinMinimizatimizatioionn
MetMethhodod
PresentPresenteded BByy::
Badgujar Pavan R.
( M. Pharm II nd Sem )
DEPARTMENT OF PHARMACEUTICAL
CHEMISTRY
R.C.Patel Institute of Pharmaceutical Education & Research,
Molecular modelling and docking
R.ARUNA SRI
Y17MPHO222
Under the guidance of
Dr. K. Ravi Kumar
M.pharm.,Ph.D.,MBA.,FAGE.,FIC.,MISTE
• HINDU COLLEGE OF PHARMACY
• AMARAVATHI ROAD, GUNTUR – 522 002, A.P.

2.  Molecular modelling is a Theoretical methods and computational
techniques use to mimic the behavior of molecules and molecular
system.
 Molecular modelling helps the scientist to visualize molecule, to
discover new compounds for drugs.
 The common feature of molecular modelling technique is the
atomistic level description of the molecular system.
 Goal : To develop a sufficient accurate model of the system so that
physical experiment is not necessary.
Introduction

3.  The term “ Molecular modeling’’expanded to
three-dimensional structures and to simulate , predict
and analyze the properties, the behavior of the
molecules on an atomic level to data mining and to
organize many compounds and their properties into
database and to perform virtual drug screening via 3D
database screening for novel drug compounds .

4. Molecular modeling strategies
 The three dimensional features of the
known receptor site are determined from
X-ray crystallography to design lead
molecule.
 Here, receptor site geometry is known;
the problem is to find a molecule that
satisfies some geometry constraints is
also good chemical match.
 After finding good candidates according
to these criteria a docking step with
energy minimization can be used to
predict binding strength.
 The indirect drug design
approach involves
comparative analysis of
structural features of known
active and inactive molecules
that are complementary with
a hypothetical receptor site.
 If the site geometry is not known,
as is oftenthe case, the designer
must base the design on other
ligand molecules that bind well to
the site of receptor.
Direct drug design Indirect drug design

5.  Molecular modelling or more generally computational chemistry is the
scientific field of simulation of molecular systems.
 Basically in the computational chemistry , the free energy of the system
can be used to assess many interesting aspects of the system.
 In the drug design , the free energy may be used to assess whether a
modification to a drug increase or decrease target binding site .
 The energy of the system is a function of the type and number of
atoms and their positions.
 Molecular modelling softwares are designed to calculate this
efficiently.
Computational chemistry approaches

6.  The energy of the molecules play important role in the
computational chemistry.
 If an algorithm can estimate the energy of the system,
then many important properties may be derived from it.
 On today's computer , however energy calculation takes
days or months even for simple system.
 So in practice, various approximations must be
introducing that reduce the calculations time while adding
acceptability of small effect on the result.

7. Atomistic Continuum
Quantum Mechanical Methodies
Molecular modeling models
Classical Methods
Molecular
Dynamics
Monte CarloQuantum Mechanics Molecular Mechanics
Deterministic Stochastic
Computational Tools

8.  Quantum mechanics is basically the molecular orbital calculation and
offers the most detailed description of a molecule’s chemical behavior.
 HOMO – highest energy occupied molecular orbital
 LUMO – lowest energy unoccupied molecular orbital
 Quantum methods utilize the principles of particle physics to
examine structure as a function of electron distribution.
 Geometries and properties for transition state and excited state can only
be calculated with Quantum mechanics.
 Their use can be extended to the analysis of molecules as yet
unsynthesized and chemical species which are difficult (or impossible)
to isolate.
QUNTUM MECHANICS

9.  Quantum mechanics is based on Schrödinger equation
HΨ = EΨ = (U + K ) Ψ
E = Energy of the system relative to one in which all atomic
particles are separated to infinite distances.
H = Hamiltonian for the system.
It is an “operator”, a mathematical construct that operates
on the molecular orbital , Ψ ,to determine the energy.
U = Potential energy
K=Kinetic energy
Ψ = Wave function describes the electron distribution around the
molecule.

10. Born-Oppenheimerapproximation
 In currently available software, the Hamiltonian above is nearly
never used.
 The problem can be simplified by separating the nuclear and
electron motions.
kinetic energy
of electrons
Attraction of
electrons to
nuclei
Repulsion
between electrons

11.  The term ab initio is Latin for “from the beginning” premises of
quantum theory.
 This is an approximate quantum mechanical calculation for a
function or finding an approximate solution to a differential
equation.
 In its purest form, quantum theory uses well known physical
constants such as the velocity of light , values for the masses and
charges of nuclear particles and differential equations to directly
calculate molecular properties and geometries. This formalism is
referred to as ab initio (from first principles) quantum mechanics.
Ab initio method

12. HARTREE FOCK APPROXIMATION
 The most common type of ab initio calculation in which the
primary approximation is the central field approximation means
Coulombic electron-electron repulsion is taken into account by
integrating the repulsion term.
 This is a variational calculation, meaning that the approximate
energies calculated are all equal to or greater than the exact
energy.
 The energies are calculated in units called Hartrees (1 Hartree =
27.2116 eV).

13.  This function is used to calculate an energy and a new set
of orbital coefficient.
 This procedure continues frequently until the energies and
orbital coefficient remains constant.
 Advantages of this method is that it breaks the many-electron
Schrodinger equation into many simpler one-electron
equations.
 Each one electron equation is solved to yield a single-
electron wave function, called an orbital, and an energy,
called an orbital energy.
Advantages:

14. Semi emperical molecular orbital methods
So Semiempirical methods are very fast, applicable to large
molecules, and may give qualitative accurate results when applied to
molecules that are similar to the molecules used for parameterization.
 Because Semiempirical quantum chemistry avoid two limitations,
namely slow speed and low accuracy, of the Hartree-Fock calculation
by omitting or parameterzing certain integrals based on experimental
data, such as ionization energies of atoms, or dipole moments of
molecules.
Rather than performing a full analysis on all electrons within the
molecule, some electron interactions are ignored .

15.  Modern semiempirical models are based on the Neglect of
Diatomic Differential Overlap (NDDO) method in which the
overlap matrix S is replaced by the unit matrix .
 This allows one to replace the Hartree-Fock secular equation
|H-ES| = 0 with a simpler equation |H-E|=0.
 Existing semiempirical models differ by the further
approximations that are made when evaluating one - and
two- electron integrals and by the parameterization philosophy.

16. Molecular mechanics
 It’s a approach of energy minimization that find stable,
low energy conformation by changing the geometry of
structure identifying a point in the configuration space at
the force on each atom vanishes.
Molecular mechanics are depends on the three parameters:
 Force field
 Parameter set: In which atomic mass , vanderwaal radii , bong
angle , dihedral angle with defines point.
 Minimizing algorithm: To calculate new geometric position are
called minimizer or optimizer

17.  It is define as a function of nuclear co-ordination i.e. the
variations in the potential energies associated with the
geometry of the molecule.
 PES should not depend upon absolute location of atoms,
only on their location relative to one another. (i.e. the
molecular geometry)
 In order to reduce computational time an empirical fit the
potential energy surface is used.

18. Force field:
 It is set of function & constant used to described potential energy of
the molecule.
 General form of force field equation ;
Epot = ∑Ebon+ ∑Eang+ ∑Etor + ∑Eoop+ ∑ Enb + ∑Eel
Where;
Epot = The total steric energy
Ebon = The energy resulting from changing the bond
length from it’s initial value calculated by Hook’s law for
deformation spring E=1/2kb(b-b0)2
[ kb = force constant for bond, b0-equilibrium bond length ,b-current
bond length]
Eang = The energy resulting from deforming a bond angle
from it’s original value .
Etor : Deforming the torsinal or dihydral angle
Eoop : Is the out of plane bending component of the steric
energy

19. StudyofElectrostatics
• It involves the study of interatction between various
dipoles.
• All atoms have partial charge eg: in C=O, C has partial
positive charge, O atom has partial negative charge.
• Two atoms that have same charge repel one another.
• In many cases molecules made of neutral groups and
two adjacent atoms have opposite charge and behave
like dipole.
• Electrostatic energy falls off much less quickly than for
vanderwaals interactions and may not be negligible
even at 30A0.

20. Moleculardynamics
 The atoms and molecules are in the constant motion and especially in
the case of biological macromolecules, these movement are concerted
and may be essential for biological function.
 And so such thermodynamic properties cannot be derived from the
harmonic approximations and molecular mechanics because they
inherently assumes the simulation methods around a systemic
minimum.
The dynamics of a system may be simplified as the movements of each
of its atoms. if the velocities and the forces acting on atoms can be
quantified, then their movement may be simulated.
 So we use molecular Dynamic simulations.

21. There are two approaches in molecular dynamics for the
simulations .
Stochastic:
It also Called as Monte Carlo simulation
Based on exploring the energy surface by randomly
probing the geometry of the molecular system.
Deterministic:
It also Called as Molecular dynamics
It actually simulates the time evolution of the molecular
system and provides us with the actual trajectory of the system.

22. It is a systematic modification of the atomic coordinates of a
model resulting in a 3-dimensional arrangement of atoms in the
model representing an energy minimum (a stable molecular
geometry to be found without crossing a conformational energy
barrier) is called energy minimization and geometry optimization .
EM used for :
Locating a stableconformation
Locating global &local energy minima
Locating saddle point
Energy minimization

23.  EM is an numerical procedure for find a minimum on the
potential energy surface starting from a higher energy initial
structure labelled "1" as illustrated in Figure .
 During EMthe geometry is change in a stepwise fashion; energy
of molecule is reduced from step 2 to 3 to 4 shown in figure .

24. The numerical minimization technique then adjust the coordinate:
Slop – (positive) : co –
ordinate is too large (point 1 )
Slope – (Negative) : co-
ordinate is too small (point 2)
Slop - (positive) : It indicate the value is co-ordinate (point2).
Slop – (Zero) : A minimum has been reached.
Slop is still positive: Co-ordinate reduced further(point 3).

25. These are all based on formulas of the type:
Where;
Xnew = The value of geometry at the
next step ( moving from step 1 to
2 in figure )
Xold = The geometry at the current step &correction .
In all these methods, a numerical test is applied to the new
geometry (Xnew) to decide if a minimum is reached .
Xnew = Xold + Correction
All the EM methods used to find a minimum on the potential
energy surface of a molecule use an alternative formula to work
in a step-wise fashion.

26. I. First-order minimization
II. Second derivative methods
Steepest descent
Conjugate gradient
Newton-Raphson

27. Utilize only values of
function
Slow and inefficient
Search algorithms
infalliable and always find
minimum
Eg : SIMPLEX
Utilizes values of a
function and its
gradients.
Currently most popular
Eg : The conjugated
gradient algorithm
 Require value of function
and its 1stand 2nd
derivatives.
 Hessian matrix
Eg :BFGSalgorithm
Newton Methods:

28. Why minimization important?
 Comparison of structures/properties
 Template forcing
 Systematic mapping of space
 Binding energies
 Docking
 Harmonic analysis
 Comparing/Fitting force fields.

29. Molecular Docking
 It is the process of predicting the protein-ligand complexes in
which the ligand molecules interact with the binding site of
receptor.
 The ligand protein interaction are various type i.e. vanderwaal,
electrostatic, hydrogen bonding.
 Successful docking methods search high dimensional space
effectively and use a scoring function that correctly ranks
candidate docking.
 Molecular docking is one of the most frequently used methods
in structure-based drug design, due to its ability to predict the
binding-conformation of small molecule ligand to the
appropriate target binding site.
 Characterisation of the binding behaviour plays an important
role in rational design of drugs as well as to elucidate
fundamental biochemical processes.

31. Key stages in Docking
Receptor selection and
preparation
• Building Receptor: The 3D
structure of receptor is
download from PDB.
This receptor must be
biologically active & stable.
• Identification of active site:
• The receptor can have many
active site but interested one
should be selected.
Ligand selection and
preparation
• Ligand can be selected from
PubChem, Chemsketch.
Docking :
• The Ligand is docked onto
the receptor and the
interaction are checked.
• The scoring functions
generates score, depending on
which the best fit ligand is
selected.

32. DOCKING TOOLS
Docking Software
• DOCK
• AutoDock
• GOLD
• GLIDE
• LigandFit
• Docking Algorithm Shape
fitting Lamarckian algorithm,
• Genetic algorithm
• Genetic Algorithm Monte
Carlo sampling
• Monte Carlo sampling

33. Types of docking
Lock and Key / Rigid Docking :
In rigid docking, both the internal geometry of the
receptor and ligand is kept fixed and docking is
performed.
Induced fit / Flexible Docking :
An enumeration on the rotations of one of the molecules
(usually smaller one) is performed. Every rotation the surface
cell occupancy and energy is calculated; later the most
optimum pose is selected.

34. RigidDocking
Historically the first approaches.
Protein and ligand are fixed.
Search for the relative orientation of the
two molecules with lowest energy.
Protein-Protein Docking
Both molecules usually considered
rigid
First apply steric constraints to limit
search space and the examine energetics
of possible binding conformations.

35. Flexibledocking
Protein-Ligand Docking
Flexible ligand, rigid-
receptor
Search space much larger
Either reduce flexible ligand to
rigid fragments connected by one
or several hinges, or search the
conformational space using
monte-carlo methods or
molecular dynamics

36. Inverse docking : small molecules of interest are dock
into library of receptor.
Covalent docking : It is used to study the covalent
character between ligand and receptor.
It provides stronger binding affinity that prolongs the
duration of biological effects.

37. Determine all possible optimal conformation for a given
complex (protein-ligand/ protein-protein)
Calculate the energy of resulting complex & of each individual
interactions.
Conformational search strategies include :
Systematic method
Random method
Simulation method

38. Scoring Function
The evaluation and ranking of predicted ligand conformations is
a crucial aspect of structure-based virtual screening.
Scoring functions implemented in docking programs make
various assumptions and simplifications in the evaluation of
modeled complexes.
They do not fully account for a number of physical
phenomena that determine molecular recognition .
Eg : Entropic effects.

39. Affinity scoring functions are applied to the energetically best
pose or in best poses found for each molecule, and comparing the
affinity scores for different molecules gives their relative rank-
ordering.
Essentially, following types or classes of scoring functions are
currently applied:
 Force-field-based scoring
 Empirical scoring functions
 Knowledge-based scoring functions
 Shape &Chemical Complementary Scores

40. De Novo Ligand design
 If one fail to find a molecule with desire interacting group
by docking method , then alternative is to construct a ligand
having the active group placed in a way that can interact
with the interaction sites identified earlier.
This ligand construction process is called de novo ligand
design
Two categories of de novo ligand design are:
– Growing
– Linking

42. applications
Generation of Chemical Structures
 Generation of conformations
Docking(Molecular interactions)
Determination of molecular properties
Determination of drug excipient interactions
Lead generation
Hit identification