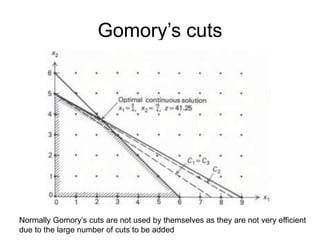
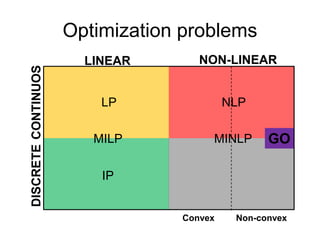
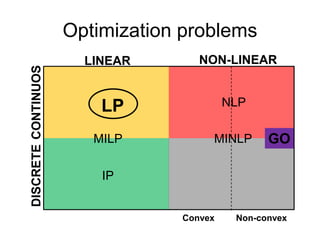
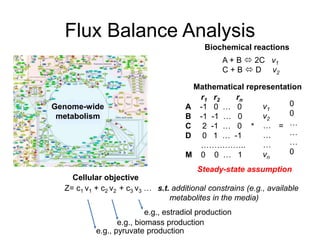
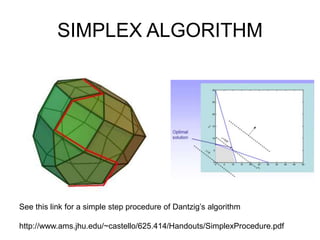
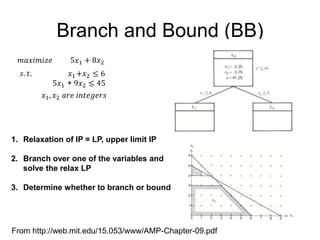
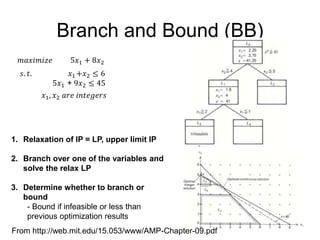
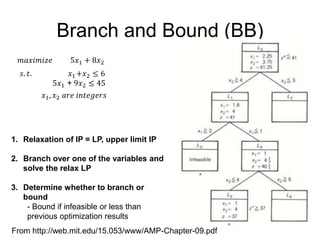
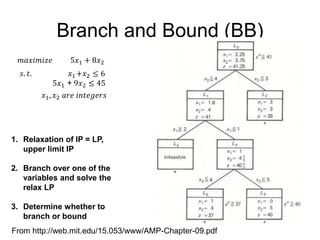
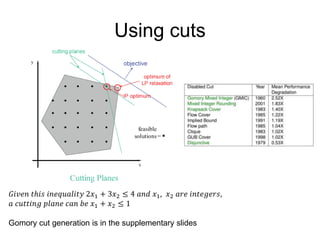
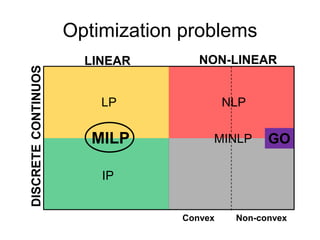
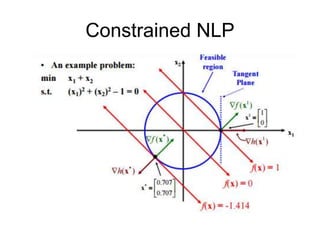
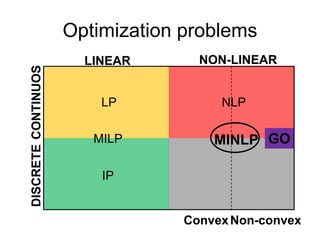
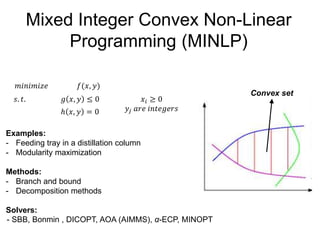
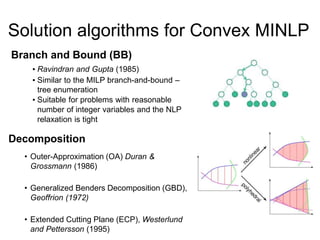
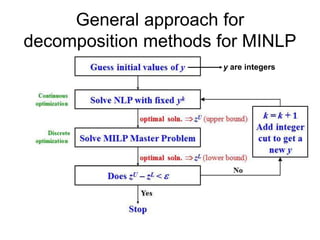
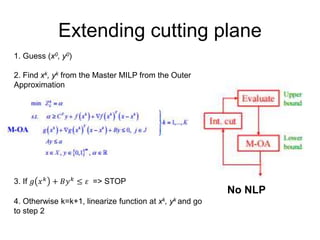
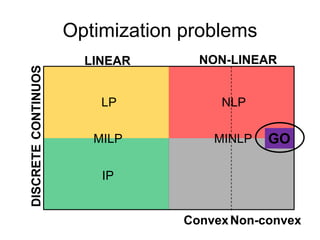
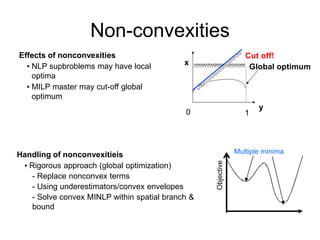
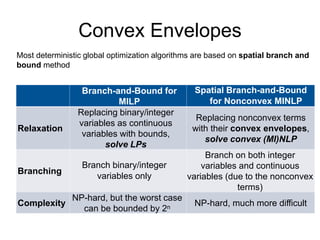
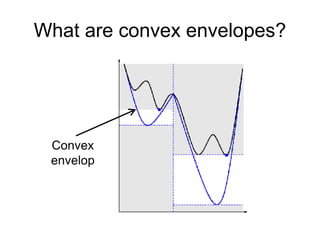
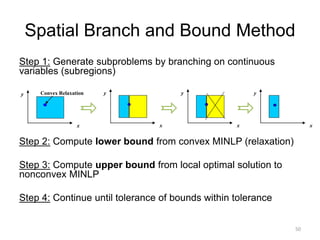
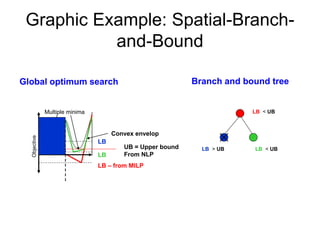
The document discusses various optimization methods for solving different types of optimization problems. It begins by defining a general optimization problem and then describes several specific problem types including linear programming (LP), integer programming (IP), mixed-integer linear programming (MILP), nonlinear programming (NLP), and mixed-integer nonlinear programming (MINLP). It provides examples and discusses solution methods like the simplex algorithm, branch and bound, and decomposition approaches.































![Sequences in time series - MINLP
min
𝑖,𝑗
𝑁,𝑀
(𝑦𝑖,𝑗 − 𝑦𝑗 )2 + 𝑀
𝑠. 𝑡. 𝑦𝑗 = 𝐴𝑗 t 𝑖 -𝐵𝑗
𝑡𝑗−1 ≤ 𝑡𝑗 𝑗 𝑖𝑛 1, 2, … . , 𝑀
𝑀 ∈ [1,2,3, … , 𝑁]
𝐴𝑗 =
𝑐𝑜𝑣(𝑦𝑗, 𝑡𝑗)
𝑉𝑎𝑟 (𝑡𝑗)
𝐵𝑗 = 𝑦𝑗- 𝐴𝑗 𝑡𝑗
𝑡0 < 𝑡𝑗 ≤ 𝑡 𝑁](https://image.slidesharecdn.com/globaloptimizationv3-150811211632-lva1-app6892/85/Global-optimization-55-320.jpg)
![Non-evolutionary genetic code - IP
min
𝑖,𝑗
𝑁
𝐶𝑖,𝑗 𝜃𝑖,𝑗
𝑠. 𝑡
𝑙
𝑠𝑖,𝑙 = 1 𝑜𝑛𝑒 𝑎𝑚𝑖𝑛𝑜 𝑓𝑜𝑟 𝑒𝑎𝑐ℎ 𝑠𝑒𝑞
𝑖
𝑠𝑖,𝑙 ≤ 42 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑒 𝑠𝑒𝑞𝑠 𝑓𝑜𝑟 𝑒𝑎𝑐ℎ 𝑎𝑚𝑖𝑛𝑜
𝑠𝑖,𝑙 ∈ [0,1]](https://image.slidesharecdn.com/globaloptimizationv3-150811211632-lva1-app6892/85/Global-optimization-56-320.jpg)