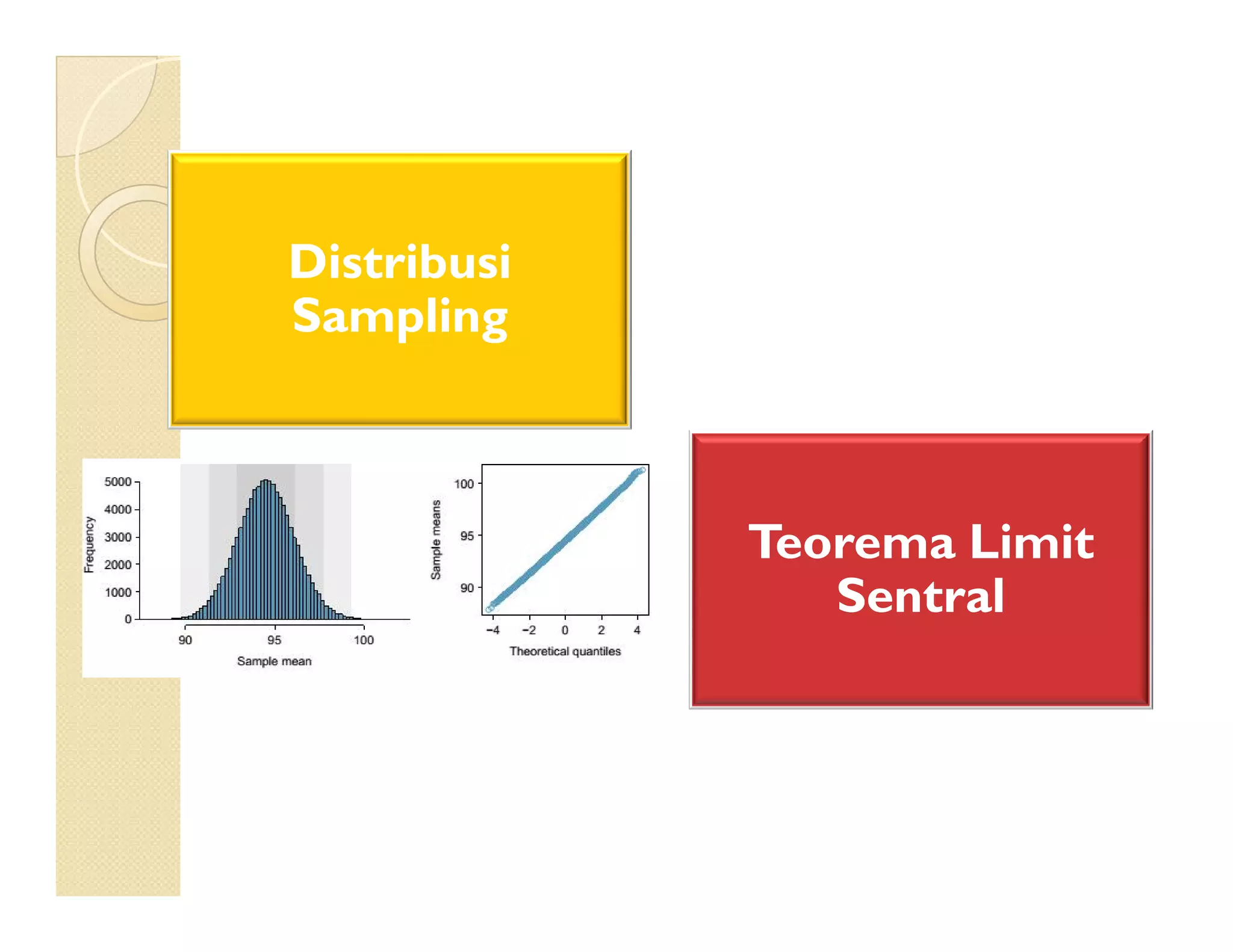
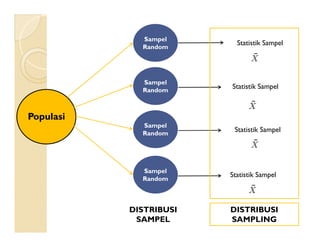
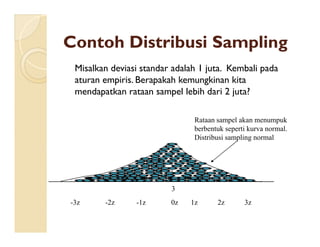
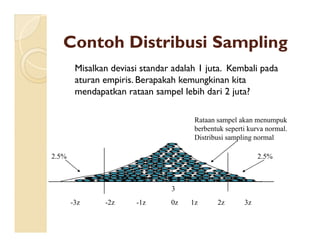
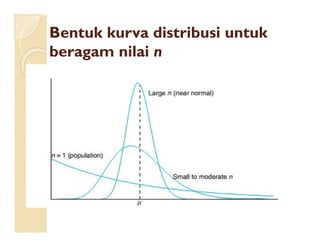
Dokumen ini menjelaskan konsep distribusi sampling dan teorema limit sentral, termasuk pentingnya sampel acak dalam analisis statistik. Juga dipaparkan metode untuk mengestimasi variabilitas dan perbandingan rataan antara dua populasi menggunakan distribusi normal atau t. Contoh konkret digunakan untuk menggambarkan penerapan teori ini dalam konteks nyata, seperti penghasilan rumah tangga dan usia aki mobil.

1. Distribusi
Sampling
Teorema Limit
Sentral

2. PERLU DIINGAT!PERLU DIINGAT!
 Populasi- totalitas dari semua
objek/ individu yg memiliki
karakteristik tertentu, jelas dan
lengkap yang akan diteliti
apa yang sedang
kita bicarakan
 Sampel- adalah sebagai
sekumpulan data yang diambil
atau diseleksi dari suatu
populasi
 Distribusi Sampling - alat
dimana kita akan beralih dari
sampel kita ke populasi
apa yang kita
miliki dengan data
kita

3. Populasi
Sampel
Random
Sampel
Random
Sampel
Statistik Sampel
Statistik Sampel
Sampel
Random
Sampel
Random
Statistik Sampel
Statistik Sampel
DISTRIBUSI
SAMPLING
DISTRIBUSI
SAMPEL

4. ContohContoh DistribusiDistribusi SamplingSampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
3

5. ContohContoh DistribusiDistribusi SamplingSampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
3

6. ContohContoh DistribusiDistribusi SamplingSampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
3

7. ContohContoh DistribusiDistribusi SamplingSampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
3

8. ContohContoh DistribusiDistribusi SamplingSampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
3

9. ContohContoh DistribusiDistribusi SamplingSampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
3

10. ContohContoh DistribusiDistribusi SamplingSampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
3

11. ContohContoh DistribusiDistribusi SamplingSampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
3

12. ContohContoh DistribusiDistribusi SamplingSampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
3

13. Contoh Distribusi Sampling
Ambil sampel berukuran 1500 keluarga dari populasi
penduduk Jakarta dan catatlah penghasilan rumah tangga.
Hasil sensus (populasi) menyatakan rataanya adalah 3
(dalam juta rupiah)
Rataan sampel akan menumpukRataan sampel akan menumpuk
berbentuk seperti kurva normal.
Distribusi sampling normal
3

14. Contoh Distribusi Sampling
Misalkan deviasi standar adalah 1 juta. Kembali pada
aturan empiris. Berapakah kemungkinan kita
mendapatkan rataan sampel lebih dari 2 juta?
Rataan sampel akan menumpukRataan sampel akan menumpuk
berbentuk seperti kurva normal.
Distribusi sampling normal
-3z -2z -1z 0z 1z 2z 3z
3

15. Contoh Distribusi Sampling
Misalkan deviasi standar adalah 1 juta. Kembali pada
aturan empiris. Berapakah kemungkinan kita
mendapatkan rataan sampel lebih dari 2 juta?
Rataan sampel akan menumpukRataan sampel akan menumpuk
berbentuk seperti kurva normal.
Distribusi sampling normal
2.5% 2.5%
3
-3z -2z -1z 0z 1z 2z 3z

16.  Permasalahannya kesempatan kita hanya satu
kali untuk mengambil sampel
 Ilustrasi diatas menunjukkan rataan hasil
sampling tidak tepat sesuai rataan populasi 
??????
sampling tidak tepat sesuai rataan populasi 
sampling error
 Jika kita dapat menentukan variabilitas (deviasi
standar) distribusi sampling, kita dapat
mengestimasi seberapa jauh rataan sampel kita
dari rataan populasi

17. TeoremaTeorema LimitLimit SentralSentral
 Jika sampel random dari pengamatan sebanyak
n, x1, x2 ,… ,xn diambil dari suatu populasi
dengan rataan µ dan variansi dan σ2 berhingga,
maka jika n cukup besar distribusi sampling
dari rataan sampel rataannya dapat didekatidari rataan sampel rataannya dapat didekati
dengan suatu fungsi normal standar.
N (z; 0,1)

18. DistribusiDistribusi SamplingSampling untukuntuk RataanRataan
&&TeoremaTeorema LimitLimit SentralSentral
 Jika adalah rataan dari sampel acak yang diambil dari suatu
populasi dengan rataan μ dan variansi σ2, maka bentuk limit
dari distribusi
Untuk n mendekati tak hingga adalah distribusi normal
N (z; 0,1)
• Aproksimasi normal untuk akan cukup baik untuk n ≥ 30,
dengan catatan distribusi populasinya tidak terlalu mencong
(skew) . Jika n < 30, Pendekatan ini masih cukup baik jika
populasinya memang tidak berbeda jauh dari distribusi
normal

19. BentukBentuk kurvakurva distribusidistribusi untukuntuk
beragamberagam nilainilai nn

20. ContohContoh
Suatu perusahaan elektronik memproduksi bola lampu yang
memiliki usia berdistribusi normal dengan rataan 800 dan standar
deviasi 40 jam. Berapa probabilitas suatu sampel random dari 16
bola lampu memiliki usia kurang dari 775 jam

21. DistribusiDistribusi SamplingSampling UntukUntuk
PerbedaanPerbedaan DuaDua RataanRataan
  menentukan perbedaan rataan antara dua populasi
 Jika terdapat dua sampel independen berukuran n1 dan n2
yang diambil secara acak dari dua populasi dengan rataan
μ1 dan μ serta variansi σ2
1 dan σ2
2, maka distribusi
sampling dari perbedaan antara dua rataan tersebut yaitu
akan mendekati distribusi normal dengan rataan dan
sampling dari perbedaan antara dua rataan tersebut yaitu
akan mendekati distribusi normal dengan rataan dan
variansi sebagai berikut:
maka
Mendekati suatu variabel
standar normal

22. ContohContoh
 Dua eksperimen yang independen dilakukan untuk menentukan
perbedaan lama kering dua tipe cat. 18 Spesimen dicat dengan tipe
1 dan lama kering (dalam jam) dicatat. Hal serupa dilakukan untuk
tipe B. Standar deviasi keduanya sama-sama 1 jam.Asumsikan rataan
lamanya cat kering kedua tipe tersebut adalah sama, tentukan
dimana adalah rataan lama kering untuk
sampel nA = nB = 18sampel nA = nB = 18

23. DistribusiDistribusi SamplingSampling untukuntuk SS22
 Jika diinginkan menghitung variabilitas dalam populasi
maka distribusi sampling S2 yang digunakan.
 Jika suatu sampel random berukuran n diambil dari
populasi normal dengan rataan dan variansi maka kita
akan memperoleh nilai statistik S2akan memperoleh nilai statistik S
 Dimana χ2 berdistribusi Chi Square dengan derajat
bebas v = n - 1 .

24. ContohContoh
 Suatu perusahaan aki mobil menjamin bahwa usia aki rata-rata
3 tahun dengan standar deviasi 1 tahun. Jika lima aki diambil
secara acak dan memiliki usia 1.9, 2.4, 3, 3. 5, dan 4.2 tahun,
apakah tepat jaminan perusahaan jika standar deviasinya 1
tahun? Asumsikan usia aki mobil berdistribusi normal
χ2 berdistribusi Chi-Square dengan derajat bebas 4. Karena 95%
dari nilai dengan v = 4 akan berada diantara 0.484 dan 11.143,
maka perusahaan sudah tepat dengan jaminan mereka bahwa
standar deviasi aki mobil tidak berbeda dari 1 tahun

26. DistribusiDistribusi tt
 Dalam beberapa kasus, misalkan dalam
eksperimen seringkali standar deviasi populasi
tidak diketahui. Untuk membuat inferensi
mengenai μ, dapat digunakan statistik berikut

27.  Misalkan X1, X2, … Xn merupakan variabel random
yang independen yang semuanya berdistribusi normal μ
dan standar deviasi σ. Selanjutnya
Maka variabel random Memiliki distribusi t dengan
derajat bebas v = n - 1

28. KurvaKurva DistribusiDistribusi––tt
 Carilah P (−t0.025< T <t0.05). Karena t0.05 adalah area
sebesar 0,05 di sisi kanan dan −t0.025 merupakan area
sebesar 0.025 di sebelah kiri, maka total area yang kita
cari adalah 1−0.05−0.025=0.925 yang terletak diantara
−t0.025 dan t0.05. Oleh karena itu
 P(−t0.025< T <t0.05)=0.925.

29. ContohContoh
 Seorang insinyur teknik kimia mengklaim bahwa
rataan populasi bahan mentah dalam suatu proses
di batch tertentu sebesar 500 grams per liter.
Untuk mengevaluasi klaim ini dia mengambil
sampel sebanyak 25 batch setiap bulan. Jika nilai t
hitung berada di antara t dan t , maka ia
sampel sebanyak 25 batch setiap bulan. Jika nilai t
hitung berada di antara −t0.05 dan t0.05, maka ia
cukup puas dengan klaim tesebut. Kesimpulan apa
yang diperoleh jika dia mengambil sampel yang
memiliki rataan 518 grams per liter dengan
standar deviasi = 40 grams? Asumsikan data
mendekati normal

30.  Dari tabel diperoleh t0.05=1.711 untuk v = 24.
Insinyur tersebut akan puas dengan klaimnya jika
sampel berukuran 25 batch menghasilkan nilai
diantara −1.711 dan 1.711. Jika μ= 500, maka
2,25 suatu nilai diatas 1.711. Probabilitas untuk mendapatkan
nilai sama atau lebih besar dari 2,25 tersebut dengan v = 24,
mendekati 0,02.
Kesimpulan: proses produksi menghasilkan produk lebih baik
dari perkiraan dia

32. KapanKapan DistribusiDistribusi--tt digunakandigunakan??
 Digunakan secara ekstensif untuk masalah
terkait menentukan inferensi tentang rataan
populasi atau perbandingan antara sampel
(apakah terdapat perbedaan rataan antara
dua sampel)dua sampel)
 Statistik T memerlukan asumsi X1,X2,...,Xn
adalah normal. Jika ukuran sampel ≥ 30 dapat
digunakan hampiran distribusi normal . Hal
ini menunjukkan S merupakan estimator
yang cukup baik bagi σ