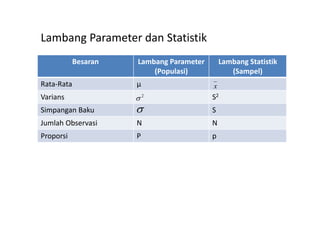
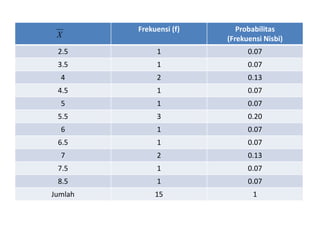
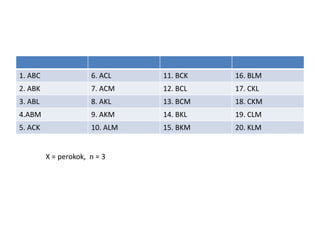
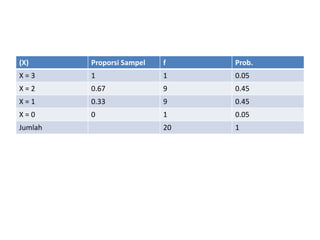
Dokumen ini menjelaskan tentang distribusi sampling dan metode pengumpulan data, termasuk sampling random dan nonrandom, serta konsep-konsep statistik terkait seperti rata-rata, varians, dan simpangan baku. Ditekankan juga pentingnya teorema limit pusat dalam distribusi sampling, dan contoh penerapan distribusi sampling untuk rata-rata dan proporsi. Selain itu, terdapat referensi untuk literatur terkait statistik industri dan inferensif.

1. Distribusi Sampling

2. Kompetensi
• Jika diberikan materi tentang distribusi
sampling, mahasiswa jurusan Teknik Industri
semester IV, akan dapat menjelaskan distribusi
sampling minimal 80% benar

3. Sub Pokok Bahasan
• Dalil Limit Pusat
• Distribusi Sampel
• Distribusi Rata-Rata
• Distribusi Proporsi

4. Definisi
• Suatu populasi terdiri atas keseluruhan
pengamatan yang menjadi perhatian
• Sampel adalah suatu himpunan bagian dari
populasi, yang dianggap bisa mewakili
populasi
• Untuk menerangkan karakteristik dari populasi
dan sampel, digunakan istilah parameter dan
statistik

5. Lambang Parameter dan Statistik
Besaran Lambang Parameter
(Populasi)
Lambang Statistik
(Sampel)
Rata-Rata µ
Varians S2
Simpangan Baku S
Jumlah Observasi N N
Proporsi P p
x
2



6. Cara Pengumpulan Data
• Sampling
Cara pengumpulan data yang hanya
mengambil sebagian elemen populasi atau
karakteristik yang ada dalam populasi
• Sensus
Cara pengumpulan data yang mengambil
setiap elemen populasi atau karakteristik yang
ada dalam populasi

7. Alasan Sampling
• Objek penelitian yang homogen
• Objek penelitian yang mudah rusak
• Penghematan biaya dan waktu
• Ukuran populasi
• Faktor ekonomis

8. Metode Sampling
• Sampling Random (Probability/Random
Sampling)
– Sampling random sederhana
– Sampling berlapis (stratified Random Sampling)
– Sampling sistematis
– Sampling kelompok (cluster sampling)
• Sampling Nonrandom
(Nonprobability/Nonrandom Sampling)

9. Sampling Random Sederhana
• Elemen-elemen populasi yang bersangkutan
homogen
• Hanya diketahui identitas-identitas dari
satuan-satuan individu (elemen) dalam
populasi, sedangkan keterangan lain
mengenai populasi, seperti derajat
keseragaman, pembagian dalam golongan-
golongan tidak diketahui, dsb

10. Stratified Random Sampling
• Adalah bentuk sampling random yang populasi
atau elemen populasinya dibagi dalam
kelompok2 yang disebut strata
• Dilakukan bila:
– Elemen2 populasi heterogen
– Ada kriteria yang akan dipergunakan sebagai dasar
untuk menstratifikasi populasi ke dalam stratum-
stratum, misalnya variabel yang akan diteliti
– Ada data pendahuluan dari populasi mengenai kriteria
yang akan digunakan untuk stratifikasi
– Dapat diketahui dengan tepat jumlah satuan-satuan
individu dari setiap stratum dalam populasi

11. Sampling Sistematis
• Adalah bentuk sampling random yang
mengambil elemen2 yang akan diselidiki
berdasarkan urutan tertentu dari populasi
yang telah disusun secara teratur

12. Cluster Sampling
• Adalah bentuk sampling random yang
populasinya dibagi menjadi beberapa
kelompok (cluster) dengan menggunakan
aturan-aturan tertentu, seperti batas-batas
alam dan wilayah administrasi pemerintahan

13. Distribusi Sampling
• Adalah distribusi dari besaran-besaran
statistik, seperti rata-rata, simpangan baku,
proporsi (persentase) yang mungkin muncul
dari sampel-sampel
– Distribusi rata-rata sampel
– Distribusi proporsi sampel
– Distribusi beda dua rata-rata
– Distribusi beda dua proporsi

14. Distribusi Rata-Rata Sampel
• Adalah dari besaran rata-rata yang muncul
dari sampel-sampel

15. Contoh Soal
• Populasi beranggotakan 6 dengan ukuran
masing: 2,3,5,6,8,9
• Diambil sampel ukuran 2, pengambilan
sampel dilakukan tanpa pengembalian
• Buat distribusi sampling rata-ratanya
• Banyaknya sampel:
15
)!
2
6
(
!
2
!
6
6
2 


C

16. • Sampel 1 : 2,3, rata-rata: 2.5
• Sampel 2 : 2,5, rata-rata: 3.5
• Sampel 3 : 2,6, rata-rata: 4
• Sampel 4 : 2,8, rata-rata: 5
• Sampel 5 : 2,9, rata-rata: 5.5
• Sampel 6 : 3,5, rata-rata: 4
• Sampel 7 : 3,6, rata-rata: 4.5
• Sampel 8 : 3,8, rata-rata: 5,5
• Sampel 9 : 3,9, rata-rata: 6
• Sampel 10: 5,6, rata-rata: 5,5
• Sampel 11: 5,8, rata-rata: 6.5
• Sampel 12: 5,9, rata-rata: 7
• Sampel 13: 6,8, rata-rata: 7
• Sampel 14: 6,9, rata-rata: 7.5
• Sampel 15: 8,9, rata-rata: 8.5

17. Frekuensi (f) Probabilitas
(Frekuensi Nisbi)
2.5 1 0.07
3.5 1 0.07
4 2 0.13
4.5 1 0.07
5 1 0.07
5.5 3 0.20
6 1 0.07
6.5 1 0.07
7 2 0.13
7.5 1 0.07
8.5 1 0.07
Jumlah 15 1
X

18. 0
0.05
0.1
0.15
0.2
0.25
Category 1
Series 1
Series 2
Series 3
Series 8
Series 9
Series 10
Series 11
Series 12
Series 13
Series 14
Series 15

19. Pada Distribusi Sampling Rata-Rata berlaku hal-
hal berikut:
• Sampel dari Populasi Terbatas
• Sampel dari Populasi Tidak Terbatas
• Teorema Limit Pusat

20. Sampel dari Populasi Terbatas
• Bila populasi terbatas yang berukuran N dan berdistribusi normal dengan
rata-rata µ dan simpangan baku rata-rata sampel yang didasarkan
pada sampel random berukuran n dan dipilih dari populasi di atas, akan
memiliki distribusi normal dengan rata-rata dan simpangan baku seperti
berikut:
– Untuk pengambilan sampel tanpa pengembalian atau n/N > 5%:
– Untuk pengambilan sampel dengan pengembalian atau
n/N ≤ 5%
 X
1




N
n
N
n
X
X




n
X
X







21. Sampel dari Populasi Tidak Terbatas
• Bila populasi memiliki ukuran yang tidak berhingga dan
didistribusikan secara normal dengan rata-rata µ dan
simpangan baku .., maka rata-rata sampel .. Yang didasarkan
pada sampel random ukuran n, dan yang dipilih dengan
pengembalian atau tanpa pengembalian dari populasi
tersebut akan memiliki distribusi normal dengan rata-rata dan
simpangan baku:
n
X
X







22. Teorema Limit Sentral
• Normalitas dari distribusi sampling rata-rata
– Jika populasi cukup besar dan berdistribusi secara
normal, maka distribusi sampling rata-ratanya akan
normal
– Jika distribusi populasi tidak normal, maka distribusi
sampling rata-ratanya akan mendekati normal, apabila
jumlah sampel cukup besar, biasanya 30 atau lebih (n≥
30)
– Distribusi normal dari rata-rata sampel memiliki rata-
rata yang sama dengan rata-rata harapan E( ) dan
simpangan baku. Nilai-nilai tersebut dapat dihitung
dari rata-rata populasi dan simpangan baku populasi
X

23. • Untuk populasi terbatas atau n/N>5%,
berlaku:
• Untuk populasi tidak terbatas atau n/N≤5%,
berlaku:
1






N
n
N
n
X
Z
atau
X
Z
X 



n
X
Z
atau
X
Z
X



 




24. Distribusi Sampling Proporsi
• Adalah distribusi dari proporsi (persentase)
yang diperoleh dari semua sampel sama besar
yang mungkin dari satu populasi

25. Contoh Soal
• Populasi beranggotakan 6 orang, 3 perokok
• A,B,C perokok dan K,L,M bukan perokok
• Diambil sampel 3 orang
• Banyaknya sampel yang dapat diambil:
20
)!
3
6
(
!
3
!
6
6
3 


C

26. 1. ABC 6. ACL 11. BCK 16. BLM
2. ABK 7. ACM 12. BCL 17. CKL
3. ABL 8. AKL 13. BCM 18. CKM
4.ABM 9. AKM 14. BKL 19. CLM
5. ACK 10. ALM 15. BKM 20. KLM
X = perokok, n = 3

27. (X) Proporsi Sampel f Prob.
X = 3 1 1 0.05
X = 2 0.67 9 0.45
X = 1 0.33 9 0.45
X = 0 0 1 0.05
Jumlah 20 1

28. 0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
Category 1
Series 1
Series 2
Series 3
Series 4

29. • Untuk pengambilan sampel dengan
pengembalian atau jika ukuran populasi besar
dibandingkan dengan ukuran sampel, yaitu
(n/N) ≤ 5%, memiliki rata-rata dan simpangan
baku:
n
PQ
n
P
P
P
p
p




)
1
(


P = proporsi kejadian sukses
Q = proporsi kejadian gagal

30. • Untuk pengambilan sampel tanpa
pengembalian atau jika ukuran populasi kecil
dibandingkan dengan ukuran sampel, yaitu
(n/N)> 5%, memiliki rata-rata dan simpangan
baku:
1
1
)
1
(








N
n
N
n
PQ
N
n
N
n
P
P
P
p
p



31. Pendekatan Normal untuk Distribusi
Sampling Proporsi
• Jika n besar maka nilai Z adalah
• Jika n sangat kecil, maka nilai Z adalah
p
P
p
Z



p
n P
p
Z



 2
1

32. Distribusi Sampling
Beda Dua Rata-Rata
• Adalah distribusi dari perbedaan dari besaran rata-rata yang
muncul dari sampel-sampel dua populasi
• Rata-Rata
• Simpangan Baku
• Pendekatan Normal
2
1
2
1


 

X
X
2
2
2
1
2
1
2
1
n
n
X
X


 


   
2
1
2
1
2
1
X
X
X
X
Z









33. Distribusi Sampling Beda Dua Proporsi
• Adalah distribusi dari perbedaan dua besaran proporsi yang
muncul dari sampel dua populasi
• Rata-Rata
• Simpangan Baku
• Pendekatan Normal
2
1
2
1
P
P
p
p 



2
2
2
1
1
1 )
1
(
)
1
(
2
1
n
P
P
n
P
P
p
p






   
2
1
2
1
2
1
p
p
P
P
p
p
Z






2
2
1
1
2
1
n
X
n
X
p
p 


Catatan:

34. Daftar Pustaka
• Fauzy, Akhmad, Statistik Industri, Penerbit
Erlangga, 2008
• Hasan, Iqbal, Pokok-Pokok Materi Statistik 2:
Statistik Inferensif, Bumi Aksara, Edisi Kedua,
2010
• Montgomery, Douglas C., George C. Runger,
Applied Statistics And Probability for Engineers,
John Wiley&Sons, 3rded., 2003
• Walpole, Ronald E., Raymond H. Myers, Ilmu
Peluang dan Statistika untuk Insinyur dan
Ilmuwan, Penerbit ITB Bandung, Edisi Ke-4, 1995