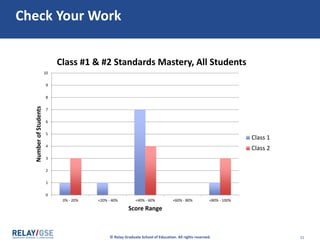
Here are the steps to create a histogram:
1) Determine the numerical ranges or "bins" to use. Here they are in 20% increments from 0-100%.
2) Count the number of data points that fall into each bin.
3) Draw columns above each bin to represent the frequencies. The column heights show the number of data points in each bin.
Let me know if any part needs more explanation!