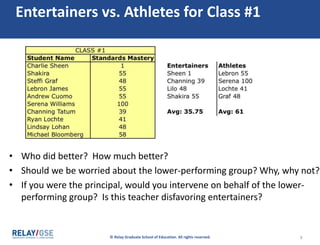
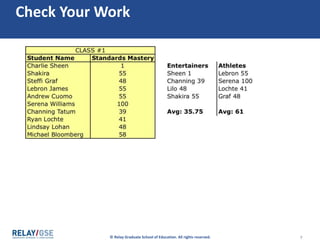
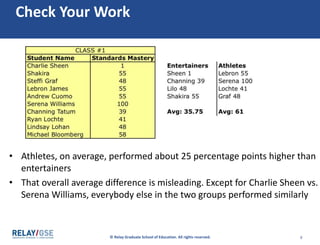
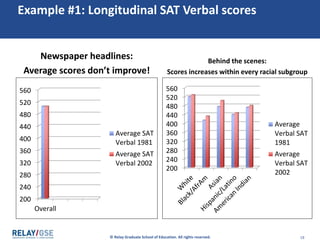
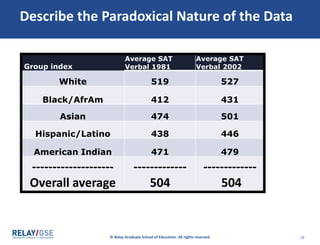
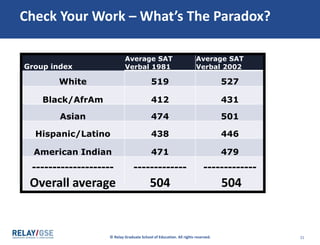
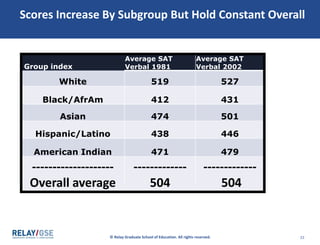
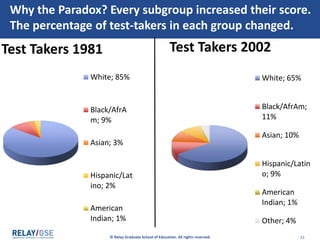
The document discusses aggregate data and descriptive statistics. It covers topics like dispersion, common mistakes in analyzing average data, Simpson's Paradox phenomenon, and properly interpreting statistical findings versus practical significance. Examples are provided to illustrate Simpson's Paradox, where averages can be misleading and hide important details that disaggregating the data by subgroups would reveal. The key lesson is that aggregate data needs to be disaggregated to tell the full story and avoid paradoxical findings.