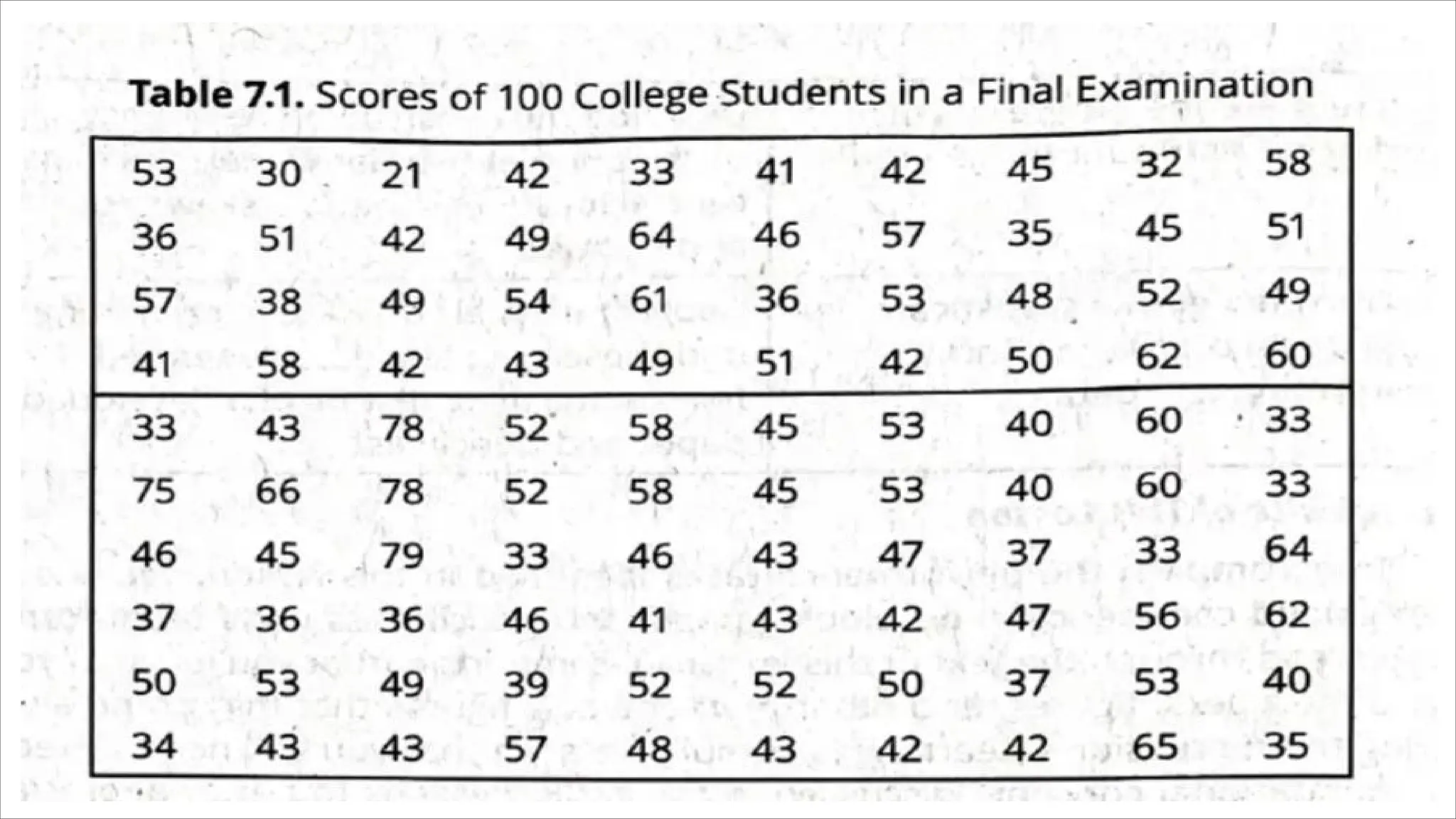
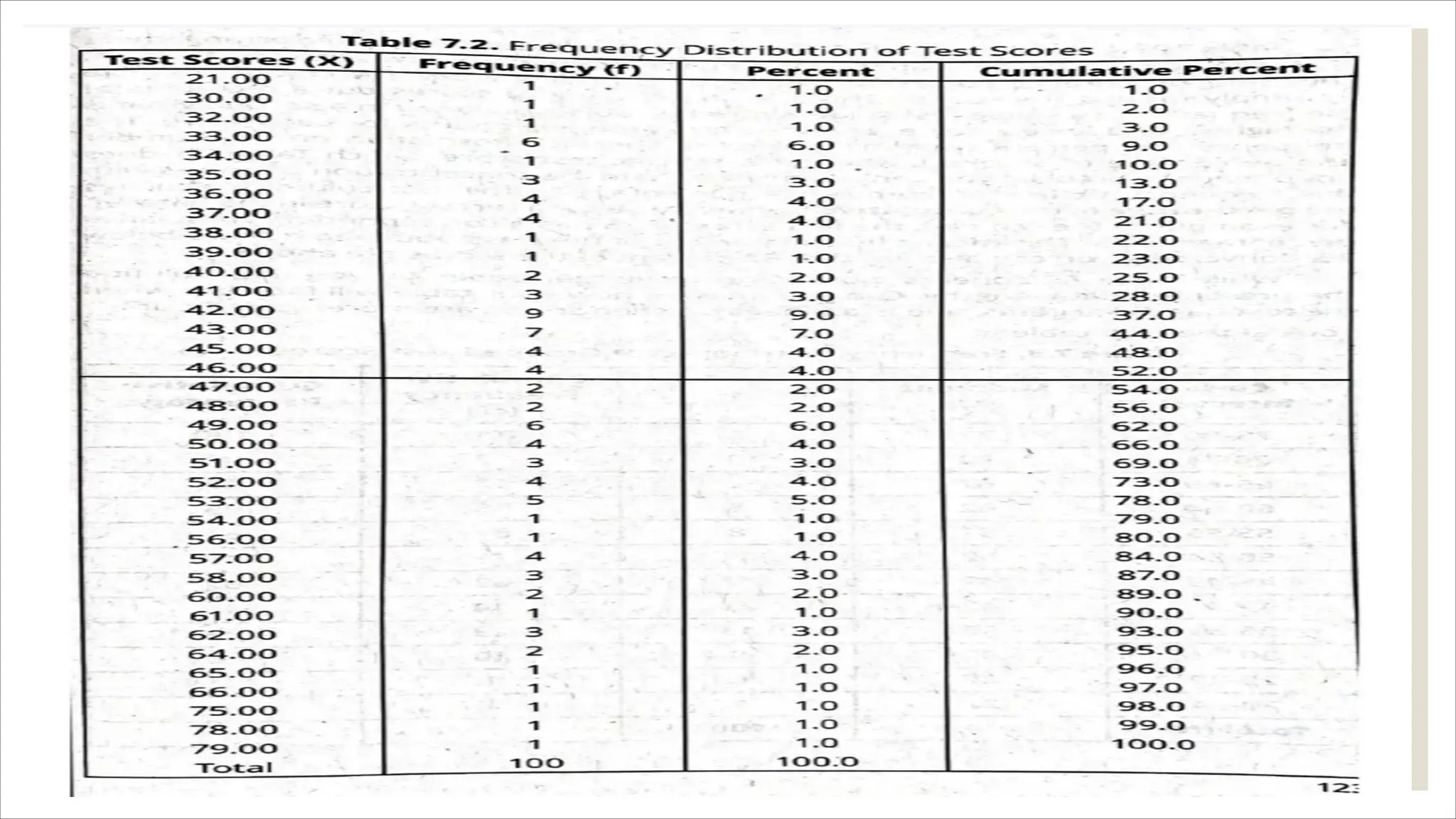
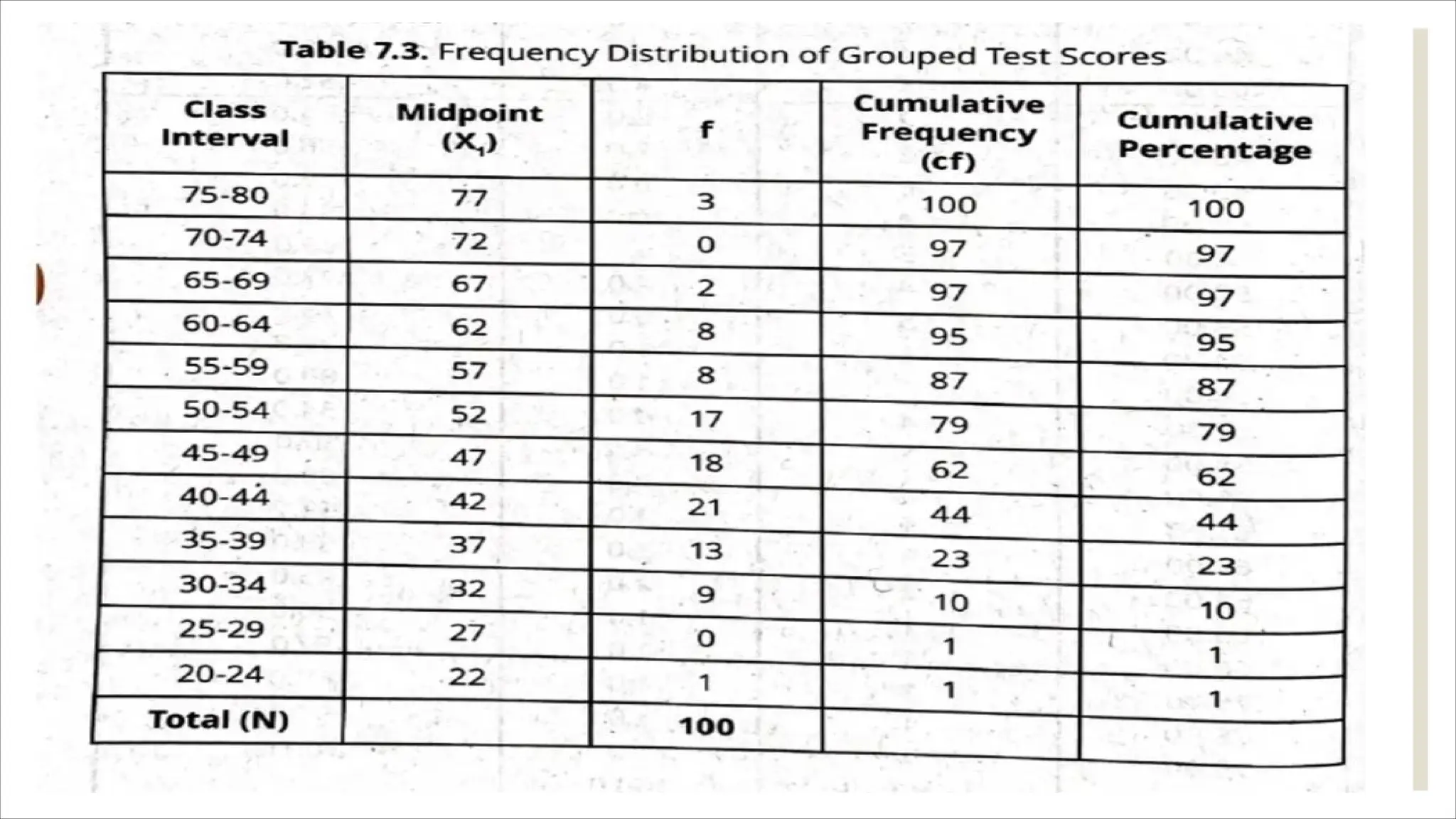
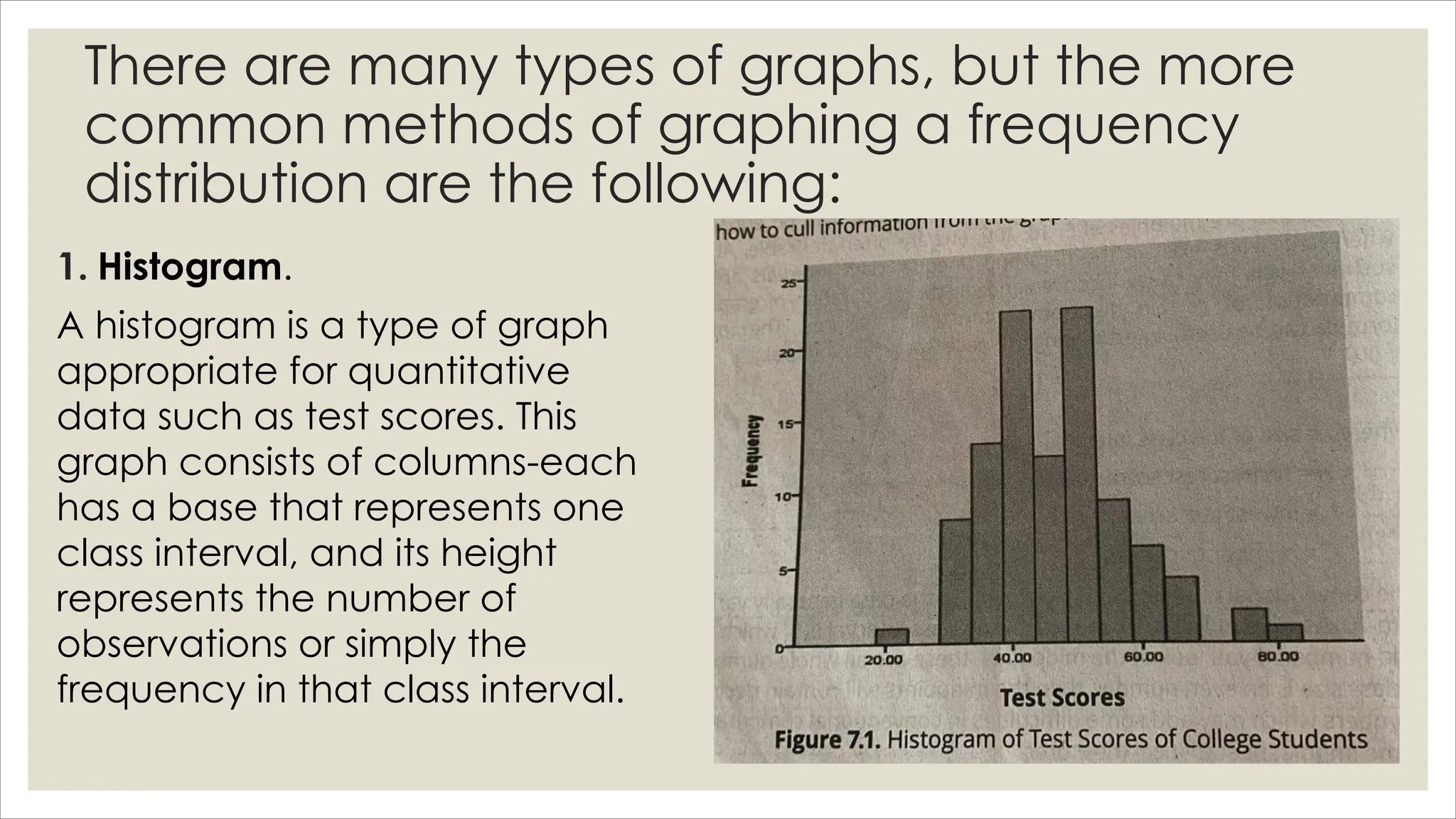
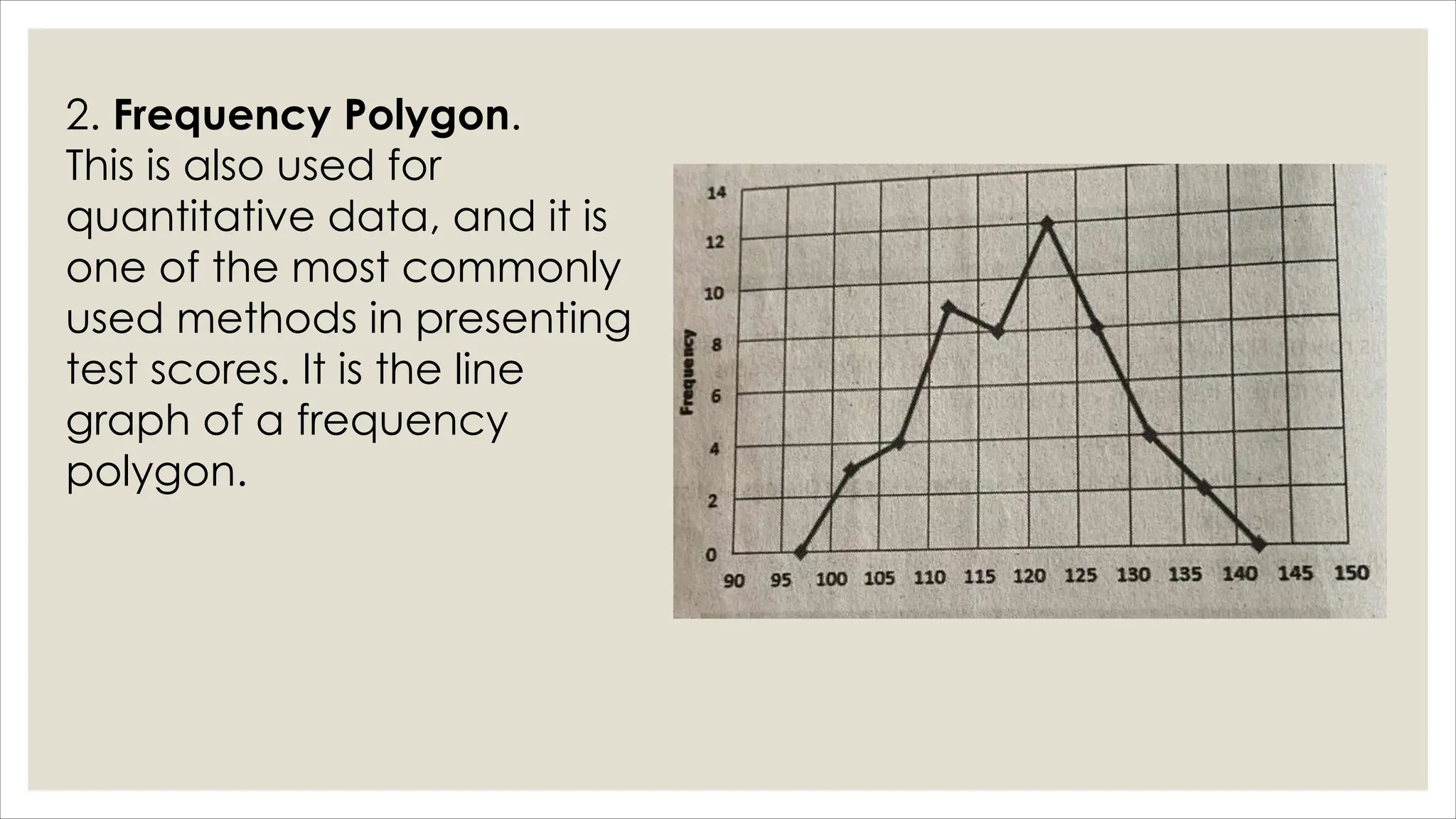
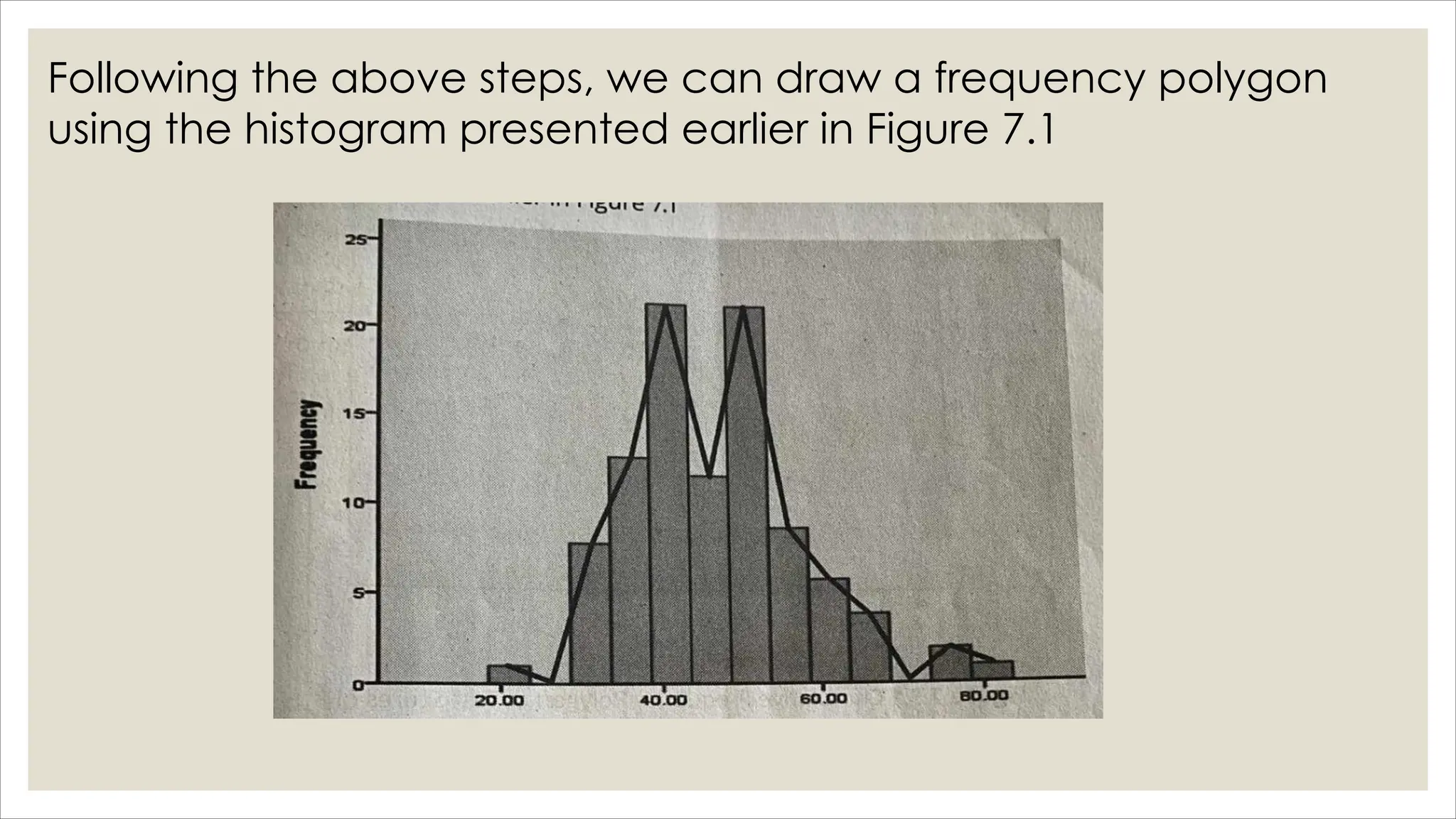
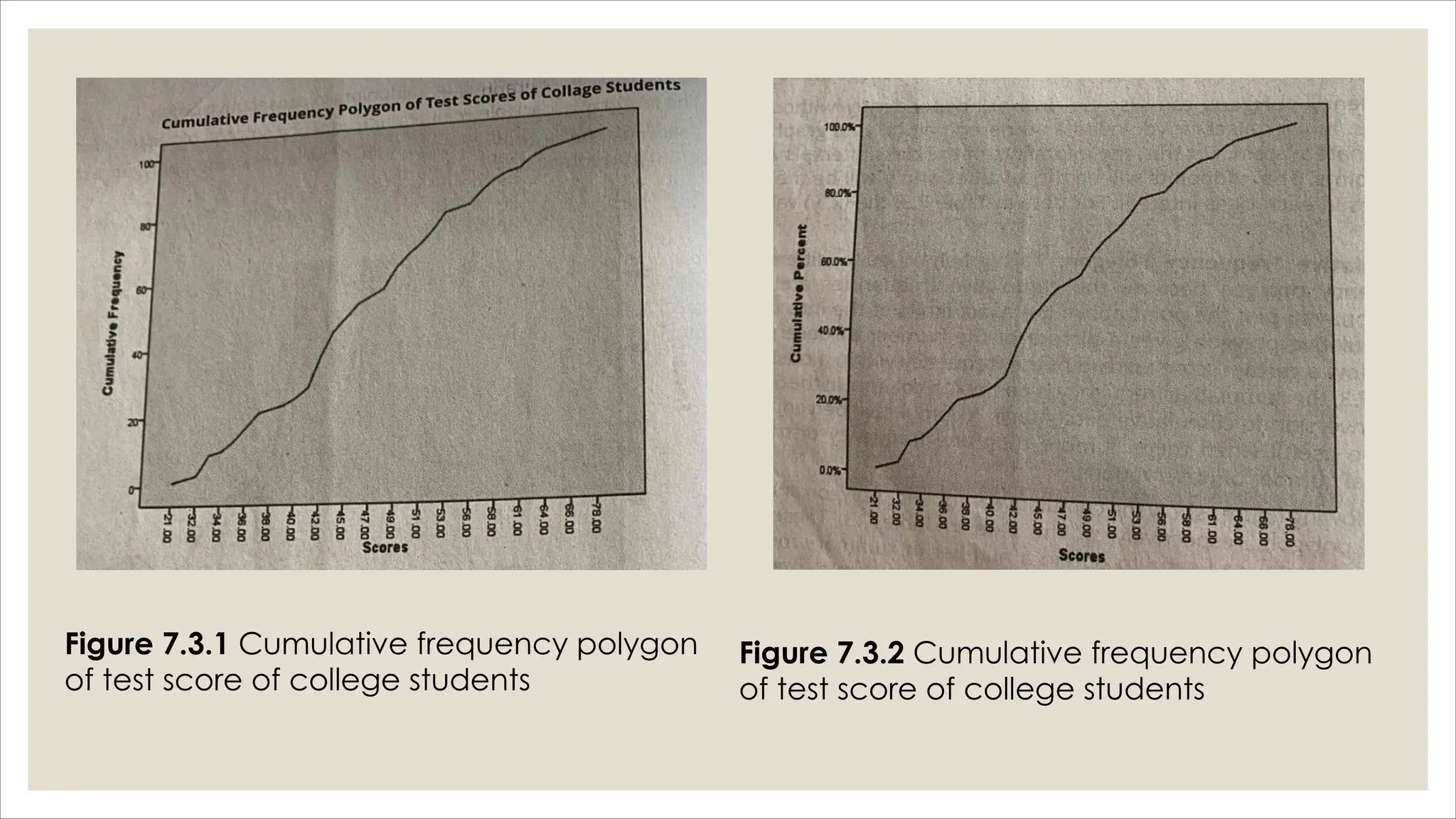
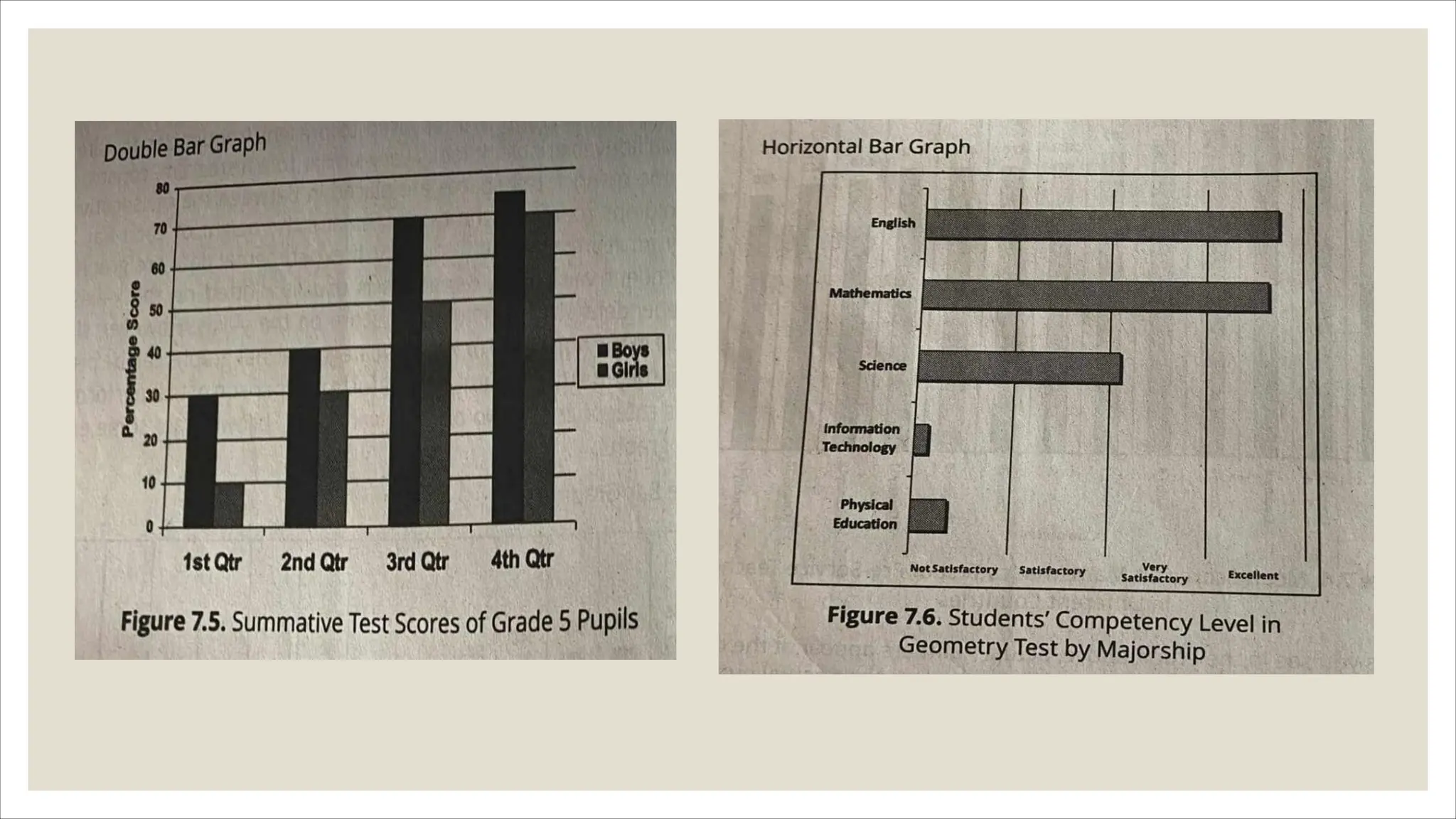
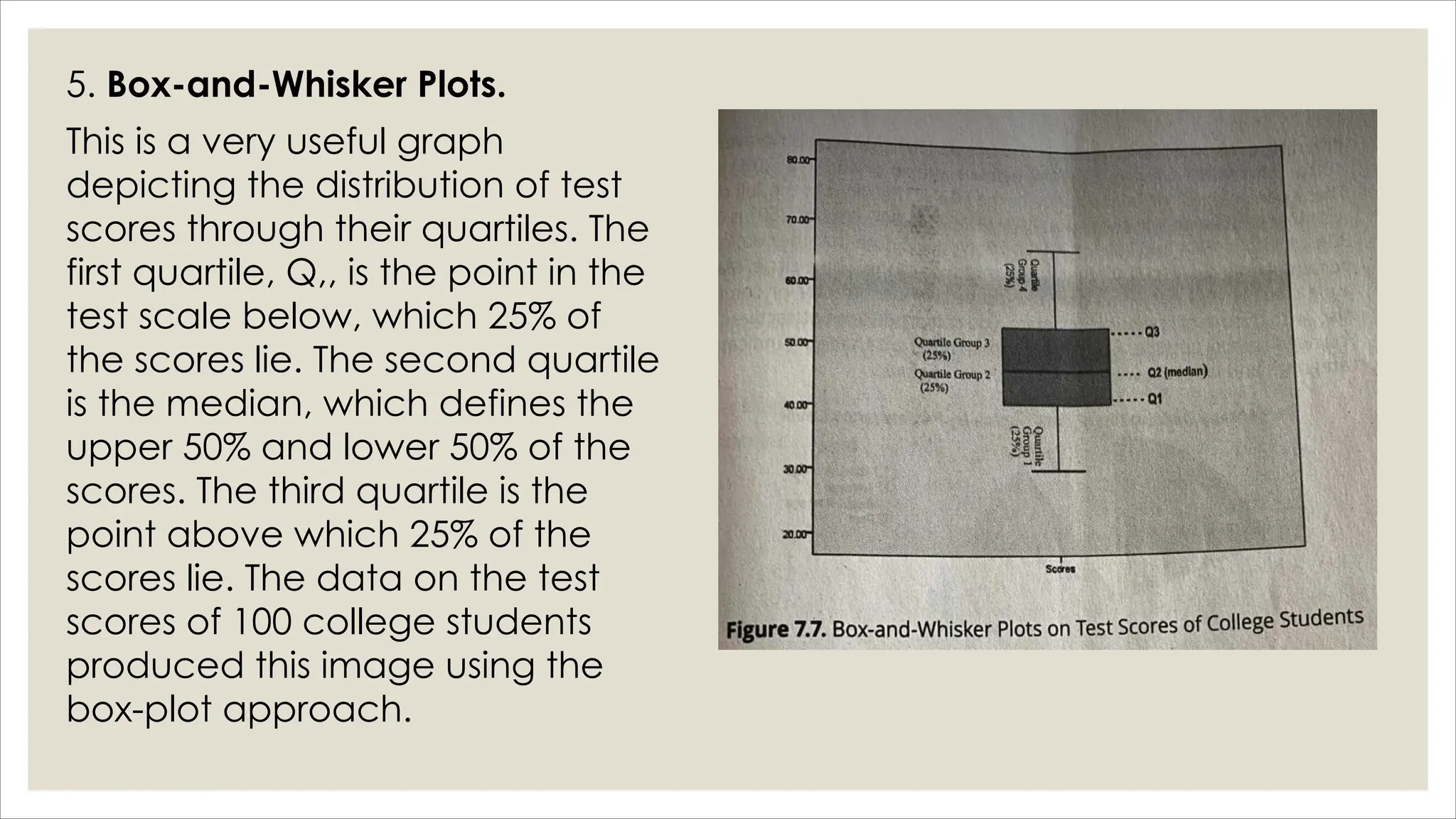
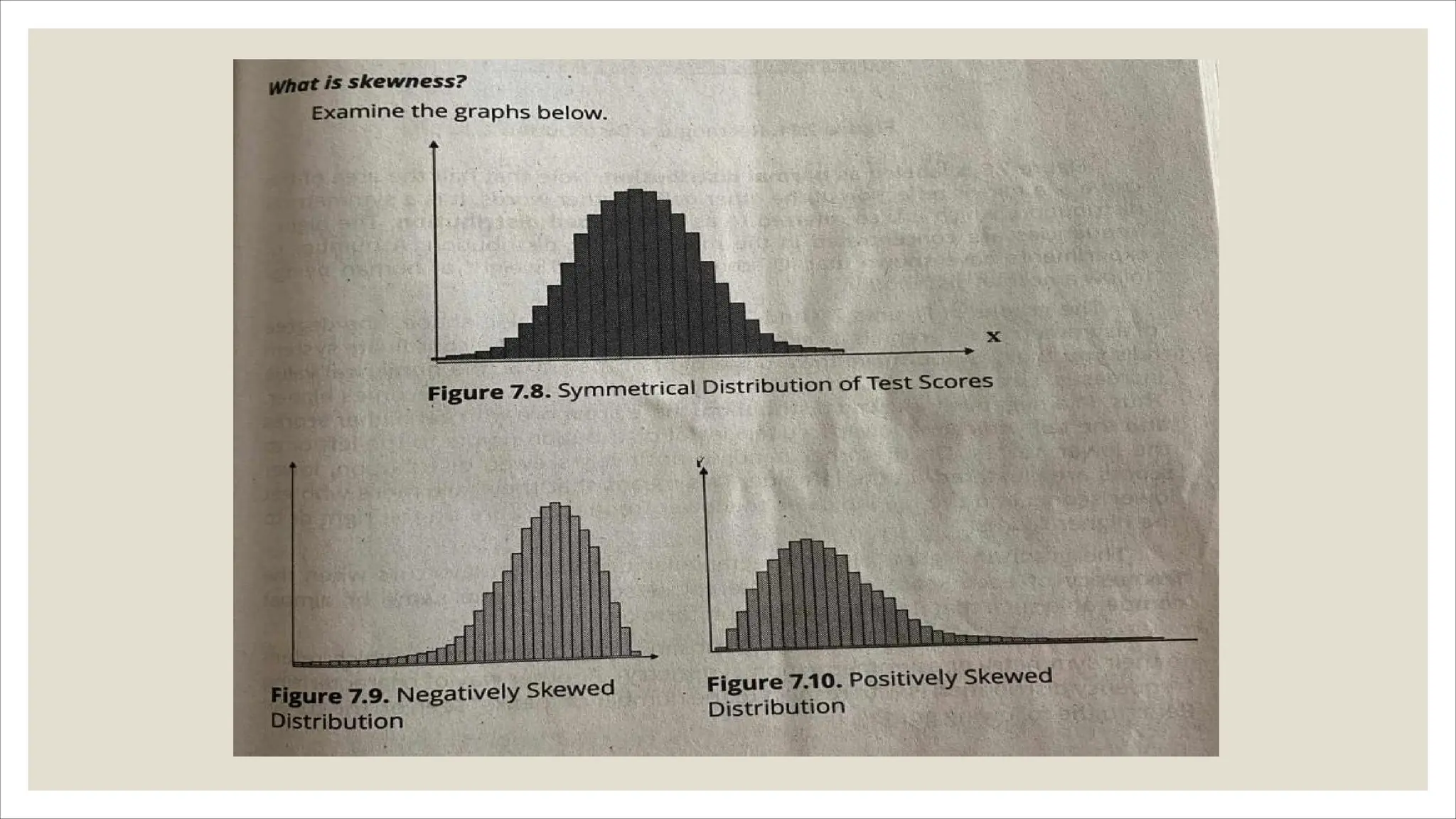
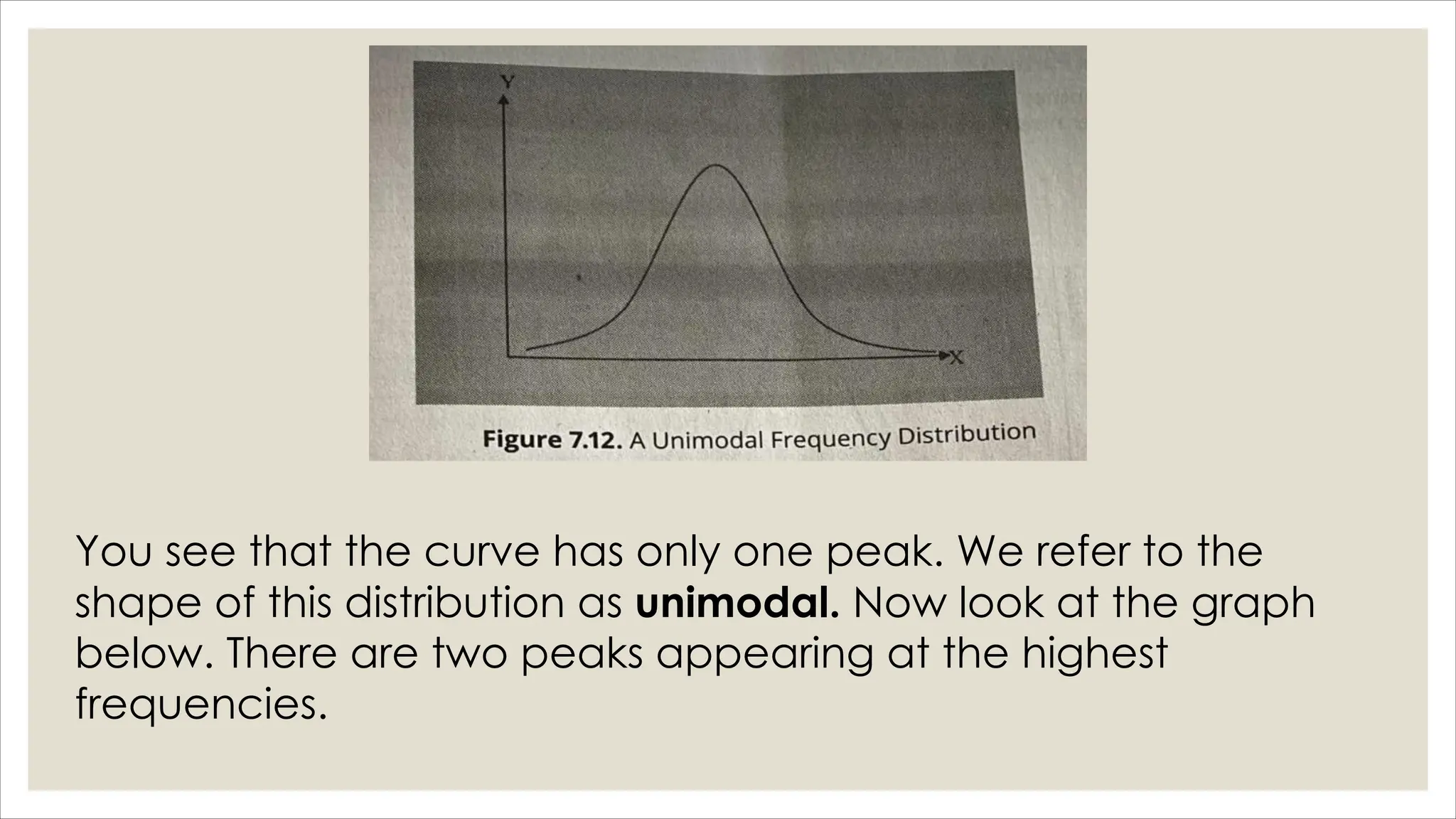
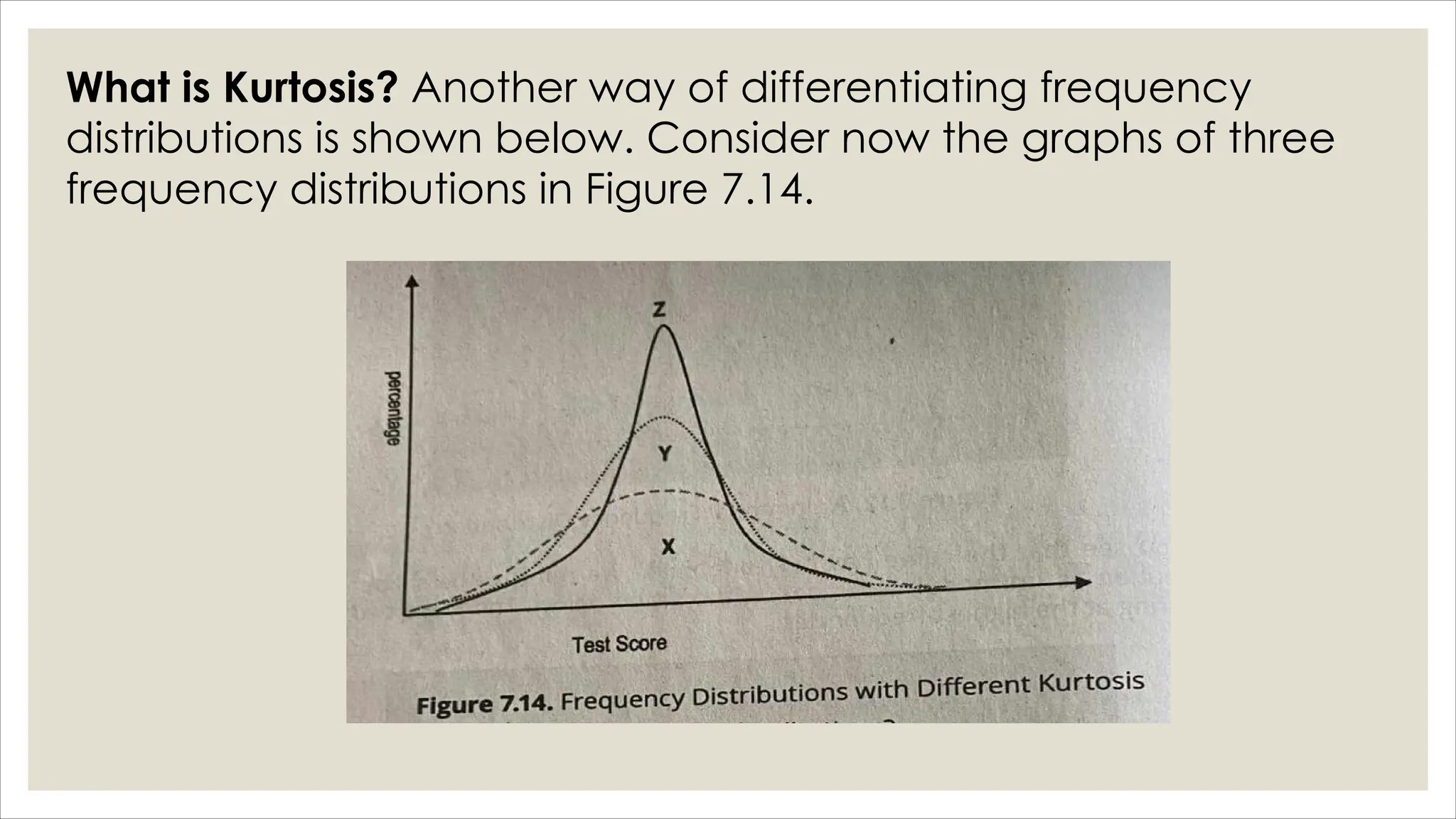
The document outlines how to organize and present test data using tables and graphs, emphasizing the importance of interpreting frequency distributions for effective communication of test results. It details different methods for graphing data, including histograms, frequency polygons, and box-and-whisker plots, while also providing conventions for constructing meaningful class intervals. Additionally, it discusses various distribution shapes, such as normal, skewed, and bimodal distributions, to highlight key characteristics in data analysis.

1. ORGANIZATION,
UTILIZATION, AND
COMMUNICATION OF
TEST RESULTS

2. Desired Significant Learning
Outcomes
In this lesson, you are expected to:
•Organize test data using tables and graphs
and
•Interpret frequency distribution of test data.

3. Significant Culminating Performance
Task and Success Indicators
•At the end of this lesson, you are expected to
present in an organized manner the test data
collected from existing database or from those
pilot tested in any of the assessment tools
implemented in the earlier lessons. Your success
in this performance task will be determined if you
have done the following:

5. Prerequisite of This Lesson
◦To accomplish the performance tasks identified
in this lesson, you should have gained
confidence in developing paper-and-pencil
tests in different forms. As you read through the
text of this lesson, it is important that you let go of
your fear of numbers, figures, and other
mathematical figures that may come along
during the discussions.

7. How do we organize and present
ungrouped data through tables?
◦As you can see in Table 7.1, the test scores
presented as a simple list of raw scores. Raw
scores are easy to get because these are scores
that are obtained from administering a test, a
questionnaire, or any inventory rating scale to
measure knowledge, skills, or other attributes of
interest.

9. Table 7.2 is a simple frequency random
arrangement of raw scores in Table 7.1. Table 7.2
is a simple frequency distribution that shows an
ordered arrangement The listing of scores can be
in descending or ascending order. You create this
table by simply tallying the scores. There is no
grouping of scores but a recording of the
frequency in a single test score.

11. ◦Apparently, the data presented in Tables 7.1 and
7.2 have been condensed as a result of
grouping of scores. Table 7.3 illustrates a
grouped frequency distribution of test scores. The
wide range of scores listed in Table 7.2 has been
reduced to 12 class intervals with an interval size
of 5. Let us consider again cumulative
percentage in the 5th row of the class interval of
55-59, which is 87. We say that, 87 percent of the
students got a score below 60.

12. Following are some conventions in presenting test
data grouped in frequency distribution:
◦ 1. As much as possible, the size of the class intervals should be equal. Class
intervals that are multiples of 5, 10, 100, etc. are often desirable. At times,
when large gaps exist in the data and unequal class intervals are used,
such intervals may cause inconvenience in the preparation of graphs and
computation of certain descriptive statistical measures. The following
formula can be useful in estimating the necessary class interval:
◦ i=H-L
C
where I = size of the class intervals
H = highest test score
L= lowest test score
C= number of classes

13. 2. Start the class interval at a value which is a multiple of
the class width. In Table 7.3, we used the class interval of
5 such that we start with the class value of 20, which is a
multiple of 5 and where 20-24 includes the lowest test
score of 21, as seen in Table 7.1.
3. As much as possible, open-ended class intervals should
be avoided, e.g., 100 and below or 150 and above.
These will cause some problems in graphing and
computation of descriptive statistical measures.

14. How do we present test data
graphically?
◦You must be familiar with the saying, “A picture is
worth a thousand words.” In a similar vein, “a
graph can be worth a hundred or a thousand
numbers.” The use of tables may not be enough
to give a clear picture of the properties of a
group of test scores.

15. There are many types of graphs, but the more
common methods of graphing a frequency
distribution are the following:
1. Histogram.
A histogram is a type of graph
appropriate for quantitative
data such as test scores. This
graph consists of columns-each
has a base that represents one
class interval, and its height
represents the number of
observations or simply the
frequency in that class interval.

16. Basic steps in SPSS application include the
following:
• Step 1. Open the Data Editor window. It is understood that
the data has already been entered into the Data editor,
following the data entry process. The assumption here is that
you already know the basics of entering data into a
statistical program.

17. ◦ Step 2. On the menu bar, click Analyze, then go to Descriptive
Statistics, then to Frequencies. This brings up the Frequencies
dialog box as seen below.

18. Step 3. To make a historgram,
do the following steps:
• Open the Data Editor
• On the menu bar, click on
Graphs Legacy Dialogs
Histogram
• Click OK

19. 2. Frequency Polygon.
This is also used for
quantitative data, and it is
one of the most commonly
used methods in presenting
test scores. It is the line
graph of a frequency
polygon.

20. You can construct a frequency polygon manually
using the histogram in Figure 7.1 by following
these simple steps:
1. Locate the midpoint on the top of each bar. Bear in mind
that the height of each bar represents the frequency in
each class interval, and the width of the bar is the class
interval.
2. Draw a line to connect all the midpoints in consecutive
order.
3. The line graph is an estimate of the frequency polygon of
the test scores.

21. Following the above steps, we can draw a frequency polygon
using the histogram presented earlier in Figure 7.1

22. 3. Cumulative Frequency Polygon. This graph is quite different
from a frequency polygon because the cumulative
frequencies are plotted. In addition, you plot the point above
the exact limits of the interval. As the such, a cumulative
polygon gives a picture of the number of observations that fall
below a certain score instead of the frequency within a class
interval.

23. Figure 7.3.1 Cumulative frequency polygon
of test score of college students
Figure 7.3.2 Cumulative frequency polygon
of test score of college students

24. 4. Bar Graph.
This graph is often used to present
frequencies in categories of a
qualitative variable. It looks very
similar to a histogram, constructed
in the same manner, but spaces
are placed in between the
consecutive bars. The columns
represent the categories and the
height of each bar as in a
histogram represents the
frequency. If experimental data
are graphed, the independent
variable in categories is usually
plotted on the x-axis, while the
dependent variable is the test
score on the y-axis.

26. 5. Box-and-Whisker Plots.
This is a very useful graph
depicting the distribution of test
scores through their quartiles. The
first quartile, Q,, is the point in the
test scale below, which 25% of
the scores lie. The second quartile
is the median, which defines the
upper 50% and lower 50% of the
scores. The third quartile is the
point above which 25% of the
scores lie. The data on the test
scores of 100 college students
produced this image using the
box-plot approach.

27. 6. Pie Graph.
One commonly used
method to represent
categorical data is the
use of a circle graph. You
have learned in basic
mathematics that there
are 360° in a full circle. As
such, the categories can
be represented by the
slices of the circle that
appear like a pie; thus,
the name pie graph.

29. Figure 7.8 is labeled as normal
distribution. Note that half the area
of the curve is a mirror reflection of
the other half. In other words, it is a
symmetrical distribution, which is also
referred to as bell-shaped distribution.
The higher frequencies are
concentrated in the middle of the
distribution. A number of experiments
have shown that IQ scores, height,
and weight of human beings follow a
normal distribution.

30. The graphs in Figures 7.9 and 7.10 are asymmetrical in shape. The degree of
asymmetry of a graph is its skewness. Basic principle of a coordinate
system tells you that, as you move toward the right of the x-axis, the
numerical value increases. Likewise, as you move up the y-axis, the scale
value becomes higher. Thus, in a negatively-skewed distribution, there are
more who get higher scores and the tail, indicating lower frequencies of
distribution points to the left or to the lower scores. On the other hand, in
positively-skewed distribution, lower scores are clustered on the left side.
This means that there are more who get lower scores and the tail indicates
the lower frequencies are on the right or to the higher scores.
The graph in Figure 7.11 is a rectangular distribution. It occurs when the
frequency of each score or class interval of scores are the same or almost
comparable such that it is also called a uniform distribution.

31. You see that the curve has only one peak. We refer to the
shape of this distribution as unimodal. Now look at the graph
below. There are two peaks appearing at the highest
frequencies.

32. We call this bimodal distribution. For those with more than two
peaks, we call these multimodal distribution. In addition,
unimodal, bimodal, or multimodal may or may not be
symmetric. Look back at the negatively-skewed and positively-
skewed distributions in Figures 7.9 and 7.10. Both have one
peak; hence, they are also unimodal distributions.

33. What is Kurtosis? Another way of differentiating frequency
distributions is shown below. Consider now the graphs of three
frequency distributions in Figure 7.14.

34. Thank you for LisTening!
Reporters:
Crislyn Macabenta
Farah Mae Titoy
Princes Aize Ompad