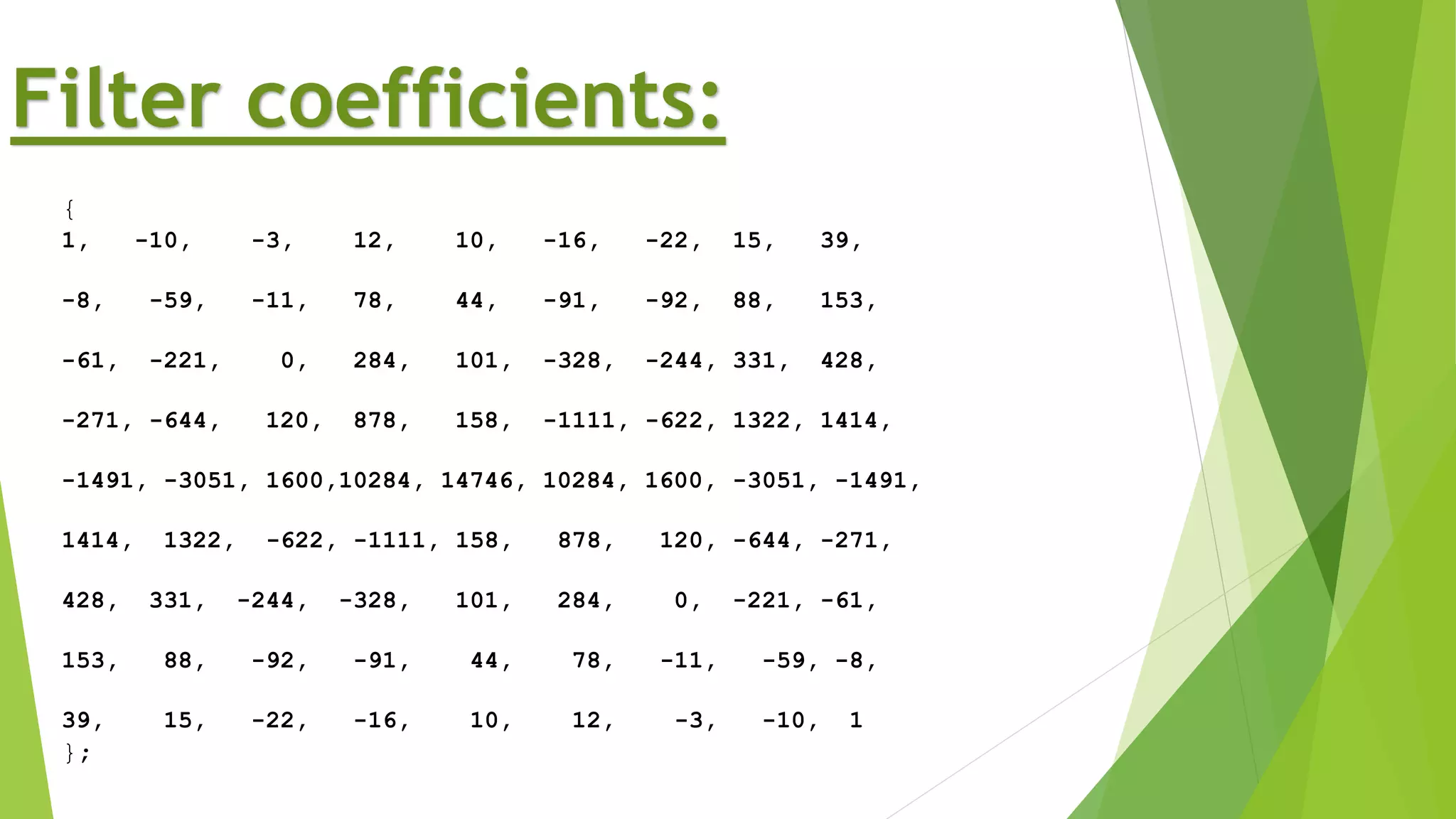
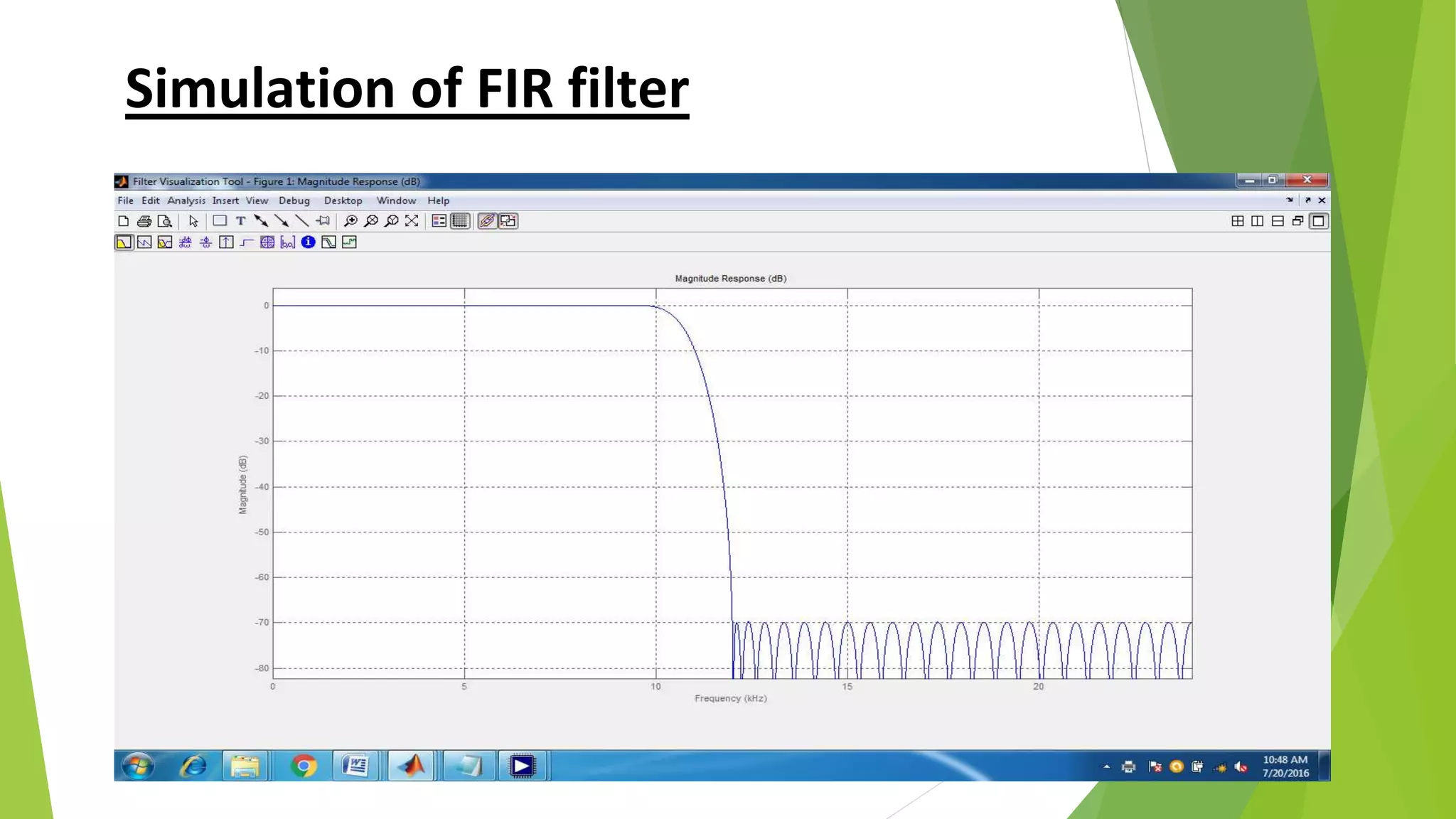
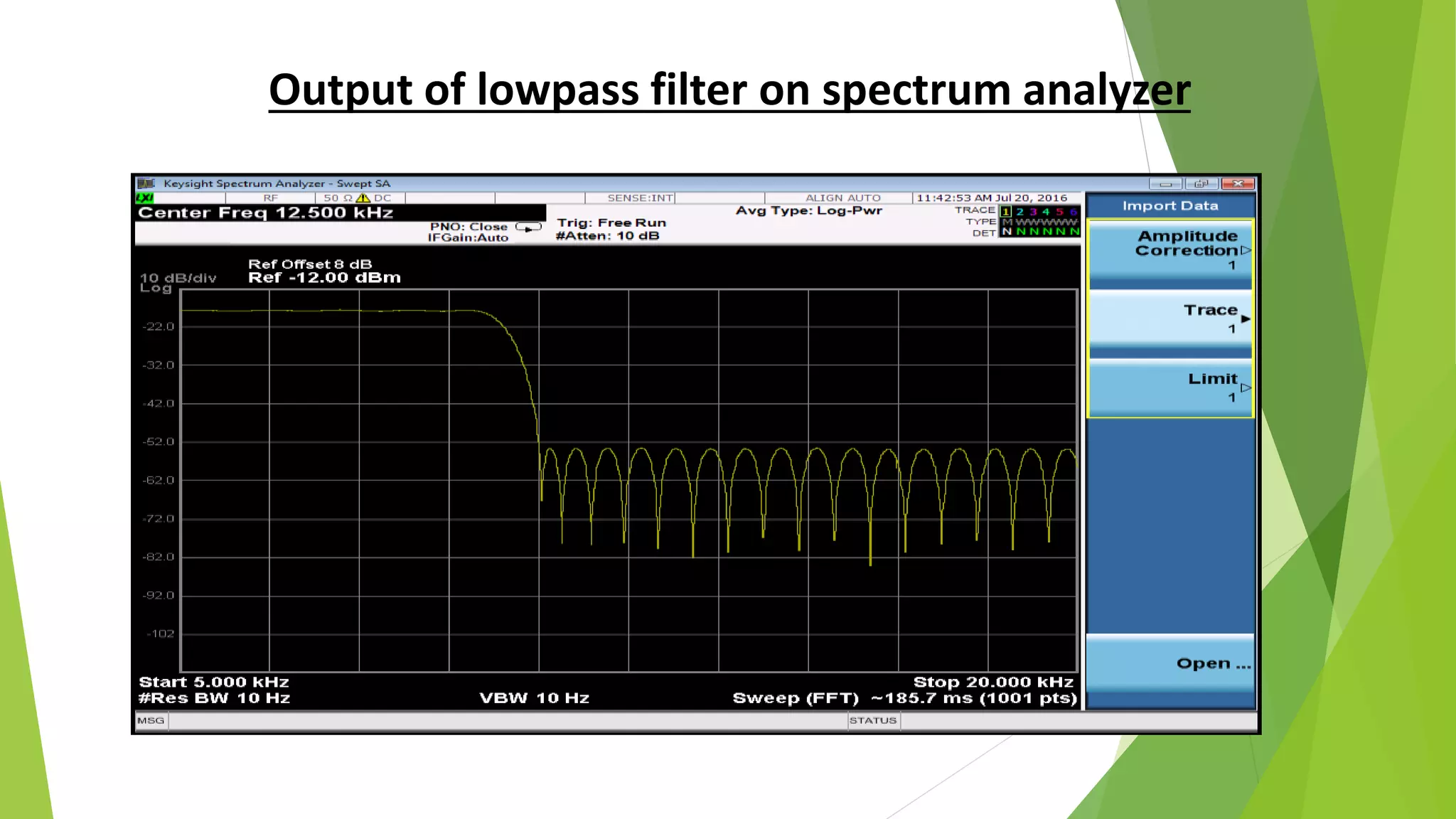
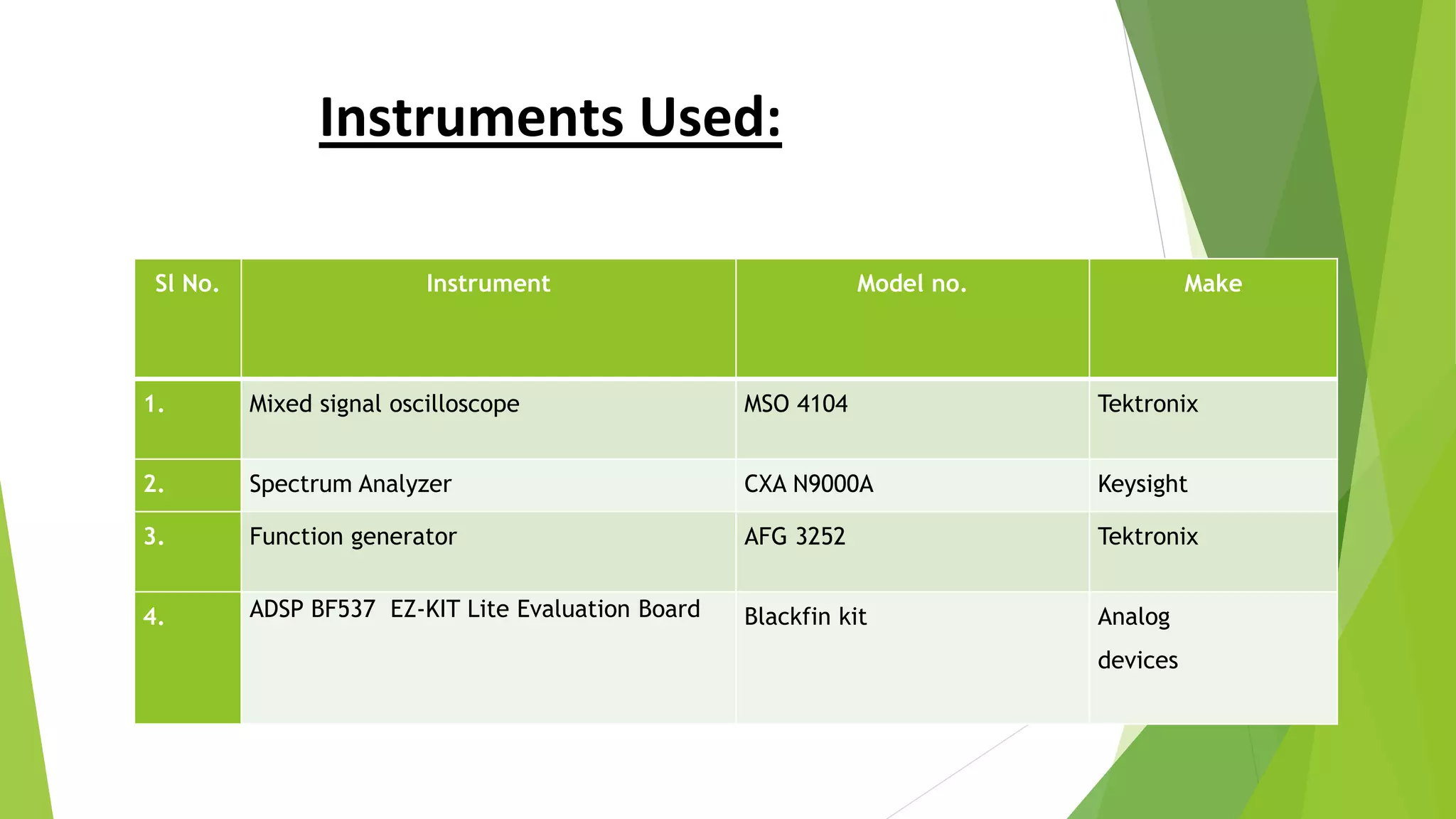
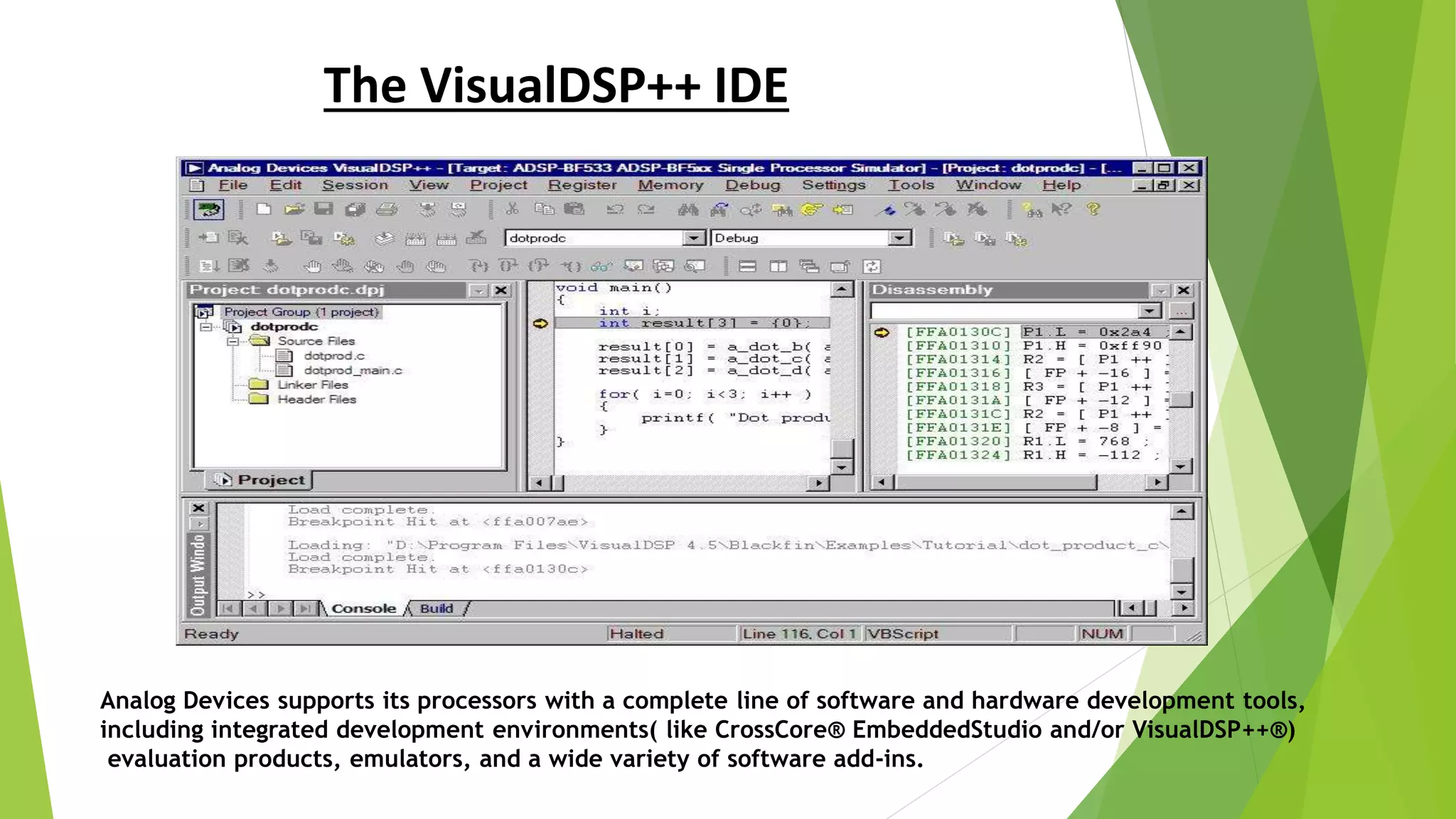
The document describes a project to implement a finite impulse response (FIR) filter on an ADSP-BF537 digital signal processor. It provides background on FIR filters and their properties. The project involved generating filter coefficients in Matlab, programming the FIR algorithm on the DSP board using tools like VisualDSP++, and simulating the lowpass filter output on a spectrum analyzer. Key instruments used included an oscilloscope, spectrum analyzer, function generator, and an evaluation board with the Blackfin DSP processor.

1. PROJECT REPORT
“Implementation of FIR Filter on ADSP-BF537
DSP Processor”
(From- 08 June 2016 to 21 July 2016)
At
Defense Electronics Applications Laboratory (DEAL)
Dehra Dun ABHISHEK DABRAL
Roll No. 130970102002
B.Tech, 3rd Year ECE
THDC-Institute Of Hydropower
Engineering And Technology,
New Tehri, Uttarakhand

2. D.R.D.O(DEFENCE RESEARCH &
DEVELOPMENT ORGANISATION)
Defence Research & Development Organisation (DRDO) works under Department of
Defence Research & Development of Ministry of Defence .DRDO dedicatedly working
towards enhancing self-reliance in Defence Systems and undertakes design &
development leading to production of world class weapon systems and equipment in
accordance with the expressed needs and qualitative requirements laid down by three
services . DRDO while striving to meet the cutting edge weapons technology requirements
provides ample spinoff benefits to the society at large thereby contributing to nation
building.

3. INTRODUCTION
• One of the most important application of digital signal processing in communication
equipment is filtering.
• A digital filter is a system that performs mathematical operations on a sampled,
discrete time signal to reduce or enhance certain aspects of that signal.
• Filters are required to select the desired signal and reject unwanted signals and noise.
• Actual filtering is not done by manual calculations, the coefficients of filters are
calculated using softwares which allows the designer to examine frequency response
and other parameters.

4. Finite Impulse-Response
(FIR)Filter
 An Fir filter is a filter whose impulse response is of finite duration, because it
settles to zero in finite time.
 The impulse response of FIR filter is equal to its coefficients .
 The value of each output sequence is a weighted sum of most recent input
values which is also called convolution.
yn =
i=0
N−1
xn−ihi

5. X(n)
Taking the z-transform gives:
Y (z) = 𝑖=1
𝑁−1
ℎ𝑖 X(z)z-1
Block Diagram of Finite Impulse Response (FIR) filter
And the transfer function is,
𝑯 𝒛 =
𝒀(𝒁)
𝑿(𝒛)

6. Properties:
A FIR filter has a number of useful properties which sometimes make it preferable to an infinite impulse
response (IIR) filter. FIR filters:
 Require no feedback. This means that any rounding errors are not compounded by summed iterations. The
same relative error occurs in each calculation. This also makes implementation simpler.
 Are inherently stable, since the output is a sum of a finite number of finite multiples of the input values, so
can be no greater ∑bi times the largest value appearing in the input.
 They can easily be designed to be linear phase by making the coefficient sequence symmetric. This property
is sometimes desired for phase-sensitive applications, for example data communications, crossover filters,
and mastering.

7. Advantages of using this technique:
 They can easily be designed to be “linear phase”.
 They are simple to implement on most DSP processors, the FIR calculation can be done by looping a single instruction.
 They are suited to multi rate applications. By multi-rate, we mean either decimation (increasing the sampling rate) or
interpolation(decreasing the sampling rate), or both. Whether decimation or interpolation, the use of FIR filter allows
some calculations to be omitted, thus providing an important computational efficiency.
 They have desirable numeric property. In practise, all DSP filter must be implemented using “finite precision”
arithmetic that is a limited no. of bits, the use of finite precision arithmetic in IIR filter can cause significant problems
due to the use of feedback, so they can using fewer bits, and the designer has fewer practical problems to be solved
related to non-ideal arithmetic.
 Complete stability at all frequencies regardless of size of filter.

8. Disadvantages of using FIR filter:
FIR filet also comes with some disadvantages as well:
 The frequency response is not as easily defined as it with IIR filters.
 The number of states required to meet a frequency specification may far larger than required for IIR
filters.
 FIR filter sometimes have a disadvantage that they require more memory and/ or calculations to
achieve a given filter response characteristics.
 Also, certain response is not practical to implement with FIR filters.
 More computational power in general purpose processor is required compared to IIR filter with
similar sharpness or selectivity.

9. Blackfin Embedded Processor ADSP-BF537
• Upto 600MHz high performance BlackFin processor.
• 132Kb on chip full speed SRAM.
• 10 stage RISC MCU/DSR pipeline.

10. The VisualDSP++ IDE
Analog Devices supports its processors with a complete line of software and hardware development tools,
including integrated development environments( like CrossCore® EmbeddedStudio and/or VisualDSP++®)
evaluation products, emulators, and a wide variety of software add-ins.

11. STEPS INVOLVED IN PROGRAMMING OF FIR FILTER:
 Generate filter coefficients in matlab for various decimating filters.
 Initialize all the parameters required in main function along with the coefficient buffers.
 Initialize all the port values required in initialize file along with defining the appropriate default functions.
 Design Fir filters using these coefficients in convolution in Process data function.
 Define all the interrupt service routines in the interrupt file used for timers along with default functions.
 Include all the necessary header files and declare all the used parameters in the Talkthrough header file.

12. Algorithm for implementing filter
 Create an array h[i] storing the coefficients.
 Create another array x[n] to store the sampled signals.
REPEAT:
 Store the current sample at x[0].
 Multiply the corresponding elements of the x[n] and h[i].
 Add all the values of x[n]*h[i].
 Send the sum to the output buffer.
 Shift the values of the array x[n] by one element and store new sample at
x[0].

13. {
1, -10, -3, 12, 10, -16, -22, 15, 39,
-8, -59, -11, 78, 44, -91, -92, 88, 153,
-61, -221, 0, 284, 101, -328, -244, 331, 428,
-271, -644, 120, 878, 158, -1111, -622, 1322, 1414,
-1491, -3051, 1600,10284, 14746, 10284, 1600, -3051, -1491,
1414, 1322, -622, -1111, 158, 878, 120, -644, -271,
428, 331, -244, -328, 101, 284, 0, -221, -61,
153, 88, -92, -91, 44, 78, -11, -59, -8,
39, 15, -22, -16, 10, 12, -3, -10, 1
};
Filter coefficients:

14. Simulation of FIR filter

15. Output of lowpass filter on spectrum analyzer

16. Sl No. Instrument Model no. Make
1. Mixed signal oscilloscope MSO 4104 Tektronix
2. Spectrum Analyzer CXA N9000A Keysight
3. Function generator AFG 3252 Tektronix
4. ADSP BF537 EZ-KIT Lite Evaluation Board Blackfin kit Analog
devices
Instruments Used: