This lesson explores the Basic Theories of Information, helping students understand how information is created, processed, transmitted, and interpreted. It introduces key concepts such as data vs. information, communication models, and the information cycle (from collection to distribution). Students will learn how information flows between people, devices, and systems, and why accurate, timely, and meaningful information is important in decision-making. The lesson also touches on early and modern theories, including the role of technology in shaping how we access and use information today. By the end, students will be able to explain the nature of information and its value in both personal and professional contexts.

1. BASIC THEORIES
OF INFORMATION

2. Objectives
• Identify the computers basic data unit.
• Understand the concepts of computer data
representation, focusing on numeric data and character
codes.
• Understand the propositional calculus and solve
problems that involves logical operations.
2

3. Part 1:
Computer System

4. Data representation and processing unit

1.Binary DigIT(Bit)




Two levels of status in computer’s electronic circuits
Smallest unit that represents data inside the computer
1 bit can represent 2 values of data, “0” or “1”
2 bits can represent 4 different values



“00”, “01”, “10”, “11”
Whether the electric current passes through it or not
Whether the voltage is high or low
1 digit of the binary system represented by “1” or “0”

5. 5
(or
Table)
(or Row)
(or Column)

6. Sizes of Data
6

7. Numeric Data Representation
•The true valueof numbers are
the same
•The representation of numbers
vary
• Decimal
• Binary
• Octal
•Hexadecimal

8. Numeric data representation
BINARY number
(Radix/Base = 2)
Weight
Value
Final (true) value
DECIMAL number
(Radix/Base = 10)
Weight
Value
Final (true) value
2 1 9 9 8
104
2*104
103
1*103
102
9*102
101
9*101
100
8*100
20000 + 1000 + 900 + 90 + 8 = 2199810
1 1 0 0 1
24
1*24
23
1*23
22
0*22
21
0*21
20
1*20
16 + 8 + 0 + 0 + 1 = 2510

9. Numeric Presentation
Data
Numeric
Data
Character
Data
Binary
Numbers
Decimal
Numbers
Unpacked Decimal
Fixed Point (Integers)
Floating Point (Real Numbers)
Represented
using
decimal
arithmetic
Packed Decimal

10. Decimal digit representation
•Binary coded decimal
•Unpacked decimal format
•Packed decimal format

11. Decimal digit representation

oBinary-coded decimal (BCD) code
numbers 0 to 9 of decimal system)
Uses 4-bit binary digits (correspond to

12. Decimal digit representation
•BCD code
•Example:

13. Decimal digit representation
•Unpacked decimal format
•Uses 1 byte for each digit of decimal number •Represents
values from 0 to 9 in least significant 4 bits of
1 byte and in most significant 4 bits (zone bits)
•Half of a byte is used (excepting the least significant byte)
–where the least significant half-byte is used to store the
sign
•1100 = +ve
•1101 = -ve
•Waste of resources (eliminated by packed decimal format)

14. Decimal digit representation
• Unpacked decimal format
+789 = F7F8C9
10 16
-789 = F7F8D9
10 16

15. Decimal digit representation
oPacked decimal format



1 byte represents a numeric value of 2 digits
the least significant 4 bits represent the sign
bit pattern for the sign is the same as per unpacked
decimal format
-789
+789
= 789D16
= 789C
10
10 16

16. Binary Representation (Fixed Point)
• Fixed point
• Integer representation
•Fixed point is a data representation format used mainly when
integer type data is processed
•One word is represented in a fixed length (e.g. 16 bits and 32
bits)
•Overflow problem when attempt is made to represent a numeric
value that exceeds the fixed length allocated
•Fraction representation
•Decimal point is considered to be immediately preceded by the
sign bit

17. Binary Representation (Fixed Point)
•Fixed point
•Integer representation
•Range of values
-(2n-1) to (2n-1–1)

18. BinaryPresentation (Fixed Point)
• Fixed point
• Fraction representation

19. Binary Representation (Floating Point)
•Floating point
•Used to represent
real number type
data
•Used to represent
extremely large or
small size of data

20. •A number system is a way of counting
things. It's a way of identifying the
quantity of something.
Number System

21. Definition
• A number system is the set of symbols used to
express quantities as the basis for counting,
determining order, comparing amounts, performing
calculations, and representing value.
It is the set of characters and mathematical rules
that are used to represent a number.
•

22. Digital Number System
Many number systems are in
use in digital technology. The most
common are the decimal, binary, octal,
and hexadecimal systems.
The decimal system is definitely the
most familiar to us because we grew up
learning and using it.

23. Comparison of Representations
•System Digits
•Binary (Base 2):0,1 •Octal (Base
8):0,1,2,3,4,5,6,7 ) •Decimal (Base
10):0,1,2,3,4,5,6,7,8,9 •Hexadecimal (Base
16):0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
•Base (or radix) –the number of digits in a
particular number system

24. Decimal System
The decimal system is composed of
10 numerals or symbols. These 10 symbols
are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; using these
symbols as digits of a number, we can
express any quantity. The decimal system,
also called the base-10 system because it
has 10 digits.

25. Binary System
-in the binary system, there are only two symbols or
possible digit values, 0 and 1. This base-2 system can
be used to represent any quantity that can be
represented in decimal or other number system
-the most important one in digital systems
-compatible with digital electronics
that are on/off or true/false
Ex. 1 0 1 0 1 0 0

26. Octal Number System
-
digit would make the number an invalid octal
number)
-is based on the binary system with a 3-bit boundary
includes only the digits 0 through 7 (any other
146 –valid as octal number
148 –invalid octal number / non-octal number

27. -closely related to binary than decimal
Ex. 1 A 6
HEXADECIMAL NUMBER SYSTEM
-Uses base with 16 digits. These digits are :
0 –9, A ,B ,C ,D ,E, F
-The prefix hex means 6 and Decimal implies 10,
therefore hexa+decimal (6+10)

28. Number System Conversion
•Binary (or Octal, or Hexadecimal) to Decimal
/ Base N to Base 10
Method: Positional Notation Method
-Take the weighted sum of each digit position,
simply add together the weight of the positions
where binary (or octal, or hex) non-zero digits
occur.
-Disregard the position weights where 0’s occur
since they add nothing.

29. Number System Conversion
•Positional Weight –each digit or bit in a
number carries a particular position weight in
determining the magnitude of that number.

30. Converting from Base N to Base 10
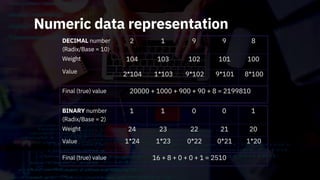
•When converting from binary [or octal, or hexadecimal] to
decimal, use the method of taking the weighted sum of each
digit position. Simply add together the weight of the positions
where binary [or octal, or hexadecimal] non-zero digits occur
and just disregard the position weights where 0s occur since
they add nothing.

31. Base N to Base 10 Examples
•
•
•
Base 2 to base 10
1. 1001.112-> ?10
Base 8 to base 10
1. 23.48-> ?10
Base 16 to base 10
1. A3.C -> ?
16 10

32. Seatwork:
A. Convert: 1.3GB = _______MB 2.5, 242,
880KB = ______MB B. Determine the true
value. Show solution.
1. 10101101 (base 2)
2. ACE(base 16)
32

33. Seatwork:
C. Represent using Unpacked BCD(in binary form)
1. +586
2. -975
D. Represent using Packed BCD(in binary form)
1. +184
2. -749
33

34. Seatwork:
E. Convert to Decimal
2
1.
2.
3
.
110011.101 =_____
376.58 =__________
10
10
124.F =__________
16 10

35. Converting from Decimal to Binary
•To convert a decimal number into a binary
number, divide it by 2 repeatedly and note the
remainders. The remainders are the bits
of the binary number. The lastremainder is
the most significant bit, and the first
remainder is the least significant bit.
For example,
13(base 10)=1101(base 2)
•
6 ÷2 = 3
3 ÷2 = 1
1 ÷2 = 0
remainder 0
remainder 1
remainder 1 MSB
13 ÷2 = 6 remainder 1 LSB

36. Converting from Decimal to Binary
•For fractional part, multiply the number by 2
and take the integer part as the remainder
then repeat the step using only the fractional
part. The remainder of the 1stmultiplication
will be considered as the MSB.
•For example,
.625(base 10) -> ? (base 2) = .101(base 2)
.625 X 2 = 1.25 remainder 1 MSB
.25 X 2 = 0.5
.5 X 2 = 1.0
remainder 0
remainder 1 LSB

37. Converting from Decimal to Octal
•To convert a decimal number into an octal
number, divide it by 8 repeatedly and note the
remainders. The remainders are the digits of the
octal number. The lastremainder is the most
significant digit, and the firstremainder is the
least significant digit.
For example,
1701(base10) = 3245(base 8)
1701 ÷8 = 212 remainder 5 LSB
•
212 ÷8 = 26 remainder 4
26 ÷8 = 3 remainder 2
3 ÷8 = 0 remainder 3 MSB

38. Converting from Decimal to Octal
•For fractional part, multiply the number by 8
and take the integer part as the remainder
then repeat the step using only the fractional
part. The remainder of the 1stmultiplication
will be considered as the MSB.

39. Converting from Decimal to Hexadecimal
•1. The first method is similar to converting a
decimal to a binary and involves dividing the
number by decimal 16 and noting the
remainders. The firstremainder is the least
significant digit and the lastremainder is the
most significant

40. Converting from Decimal to Hexadecimal
•For fractional part, multiply the number by 16
and take the integer part as the remainder
then repeat the step using only the fractional
part. The remainder of the 1stmultiplication
will be considered as the MSB.

41. Converting from Decimal to
Hexadecimal
2. The second method involves converting the
decimal number into a binary, then convert the
binary into a hexadecimalnumber. To change
the representation of the binary number to
hexadecimal, separate the digits into 4-bit
groups beginning with the least significant bit.
Then write the hexadecimal equivalent of each
group.

42. 2 ÷2 = 1remainder 0
1 ÷2 = 0remainder 1 MSB
0001 0111(base 2)=17(base 16)
0001 0111 (base 2)= 17 (base 16)

43. Converting from Binary to Hexadecimal
•To convert a binary number into its hexadecimal
form, start by grouping the digits into 4-bit groups.
Beginning with the least significant bit (all the way
to the right of the number), write the hexadecimal
equivalent of each group.
For example,
1001111101100101(base 2)=9F65(base16) 1001 1111
0110 0101 (base 2)
•
9 F 6 5 (base 16)
MSB LSB

44. Converting From Hexadecimal to Binary
•To convert a hexadecimal number into a binary, just reverse the
above process; starting all the way to the right, convert each
digit into a 4-bit binary number.

45. Converting From Binary to Octal
•To convert a binary number into its octal
form, start by grouping the digits into 3-bit
groups. Beginning with the least significant
bit (all the way to the right of the number),
write the octal equivalent of each group.
For example,
10110111011(base 2)=2673(base 8)
010 110 111 011 (base 2)
•
2 6 7 3 (base 8)
MSB LSB

46. Converting From Octal to Binary
•To convert an octal number into a binary, just reverse the above
process; starting all the way to the right, convert each digit into
a 3-bit binary number.

47. Binary Arithmetic
• Addition and subtraction of binary numbers
• Addition
•
•
•
•
0 + 0 = 0 (or 0
0 + 1 = 1 (or 1
1 + 0 = 1 (or 1
)
)
)
10
10
10
1 + 1 = 10 (or 2
10)

48. Binary Addition
Result = 1001102

49. 4. Addition and subtraction of hexadecimal
numbers
Addition




Performed starting at the lowest (first from the
right) digit
A carry to the upper digit is performed when
the result is higher than 16
Performed starting at the lowest (first from the
right) digit
A borrow from the upper digit is performed
when the result is negative
Subtraction
Hexadecimal arithmetic

50. Hexadecimal Addition
•The result is (15A4)
•First column from right
•Third column from right
1 + 8 + 1 = (In the decimal system: 10) = A
Carried from the first column
The sum of the third column is 5 and 1 is carried to the fourth column.
.
D + 7 = (In the decimal system: 13 + 7 = 20) = 16 (carried 1) + 4
The sum of the first column is 4 and 1 is carried to the second column.
•Second column from right
A + B = (In the decimal system: 10 + 11 = 21) = 16 (carried 1) + 5
16

51. Hexadecimal Subtraction
•The result is (55F)
•First column from right
•Second column from right
Since 3 –4 = –1, a borrow is performed from D in the second
digit (D becomes C).
16 (borrowed 1) + 3 –4 = F (In the decimal system: 19 –4 =
15)
C –7 = 5 (In the decimal system: 12 –7 = 5)
6 –1 = 5
.
•Third column
16

52. Binary Representation
•1’s complement and 2’s complement
representation of negative numbers

53. Binary Representation
• “1’s complement” and “2’s complement” representation of negative integers
• range of represented numeric values when n-bit binary number is represented by
adopting the “1’s complement” method:
n-1 n-1
range of represented numeric values when n-bit binary number is represented by
adopting the “2’s complement” method:
-(2
-(2
–1) to (2 –1)
) to (2n-1–1)
•
n-1

54. Binary Subtraction
Using 1’s complement
Steps:
i) To write down 1’s complement of the subtrahend.
ii) To add this with the minuend.
iii) If the result of addition has a carry over then it is dropped and an 1
is added in the last bit.
iv) If there is no carry over, then 1’s complement of the result of
addition is obtained to get the final result and it is negative.
54

55. Binary Subtraction
110101 –100101
Solution:
Minued-
Subrahend -
Carry over - 1
The required difference is 10000
1 1 0 1 0 1
0 1 1 0 1 0
0 0 1 1 1 1
1
0 1 0 0 0 0
•
55

56. Binary Subtraction
101011 –111001
Minued- 1 0 1 0 1 1
0 0 0 1 1 0
1’s complement -
1 1 0 0 0 1
•Hence the difference is –1 1 1 0
56

57. Binary Subtraction
Using 2’s complement
Steps:
(i)At first, 2’s complement of the subtrahend is found.
(ii)Then it is added to the minuend.
(iii)If the final carry over of the sum is 1, it is dropped and the result is
positive.
(iv)If there is no carry over, the two’s complement of the sum will be
the result and it is negative.
57

58. Binary Subtraction
110110 –10110
Now, 2’s complement of 010110 is (101101 + 1) i.e.101010. Adding
this with the minuend.
1
1
1 1
1 0 1 1 0
0 1 0 1 0
0 0 0 0 0
Minuend
2’s complement of subtrahend
Result of addition
•After dropping the carry over we get the result of subtraction to be
100000.
58

59. Binary Subtraction
(ii) 10110 –11010
Solution:
2’s complement of 11010 is (00101 + 1) i.e. 00110. Hence
Minued-
2’s complement of subtrahend -
Result of addition -
1 0 1 1 0
0 0 1 1 0
1 1 1 0 0
As there is no carry over, the result of subtraction is negative and is obtained by
writing the 2’s complement of 11100 i.e.(00011 + 1) or 00100.
Hence the difference is –100.
•
•
59

60. Bit Shift Operations
• Using bit shifts, the multiplication and division of numeric
values can be easily performed
Shifting a binary digit 1 bit to the left, its value is doubled.
n
•
When a binary number is shifted
value is increased 2ntimes
When a binary number is shifted n bits to the right, its former
value decreases 2-ntimes (divided by 2n)
bits to the left, its former

61. Proposition Logic
•A is an assertion that something is the
proposition
case. We use sentences to express propositions.
Examples:
(i) The following sentences express the same
proposition:
-“It is raining”
(ii) The following sentences express the same
proposition:
-“John loves Mary”
-“Mary is loved by John”

62. •A
operator that joins them.
joins two propositions to form a new,
logical operator
complex, proposition.
•The truth valueof the new proposition is determined by the
truth values of the two propositions being joined and by the
Logical Operation

63. oTruth tables for Negation
p
T
F
¬p
F
T p
T
T
F
F
q
T
F
T
F
Not p
F
F
T
T
Logical Operation

64. oTruth tables for Logical product
p
T
T
F
F
q
T
F
T
F
p ٨q
T
F
F
F
Logical Operation

65. oTruth tables for Logical sum
p
T
T
F
F
q
T
F
T
F
p ۷q
T
T
T
F
Logical Operation

66. oTruth tables for Exclusive OR
p
T
T
F
F
q
T
F
T
F
p q
F
T
T
F
Logical Operation

67. oTruth tables for Negative AND (NAND)
P
T
T
F
F
Q
T
F
T
F
P.Q
T
F
F
F
Not (P.Q)
F
T
T
T
Logical Operation

68. •Logical expression laws
oLogical symbols
Logical sum
Exclusive OR
Meaning
OR
EOR
۷
Symbols
¬
٨
+ X+Y
Notation example
Negation
Logical product
NOT
AND
¯
· X·Y
X Y
Logical Operation

69. Absorption law
Restoring law
De Morgan’s law
Logical sum law
Exclusive OR law
Commutative law
Associative law
Distributive law
X + X = X, X + = 1, X + 0 = X, X + 1 = 1
X X = 0, X = 1, X 0 = X, X 1 =
X + Y = Y + X, X · Y = Y · X
X + (Y + Z) = (X + Y) + Z, X· (Y · Z) = (X · Y) · Z
X + (Y · Z) = (X + Y) · (X + Z)
X ·(Y + Z) = (X · Y) + (X · Z)
X + (X · Y) = X, X · (X + Y) = X
= X
= · , = +
Logical product law X · X = X, X · = 0, X · 0 = 0, X · 1 = X
Logical Operation
- Laws of logical expressions