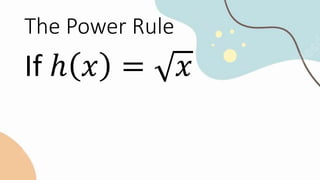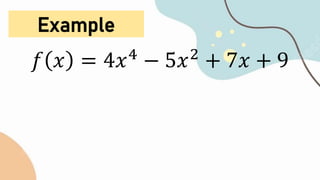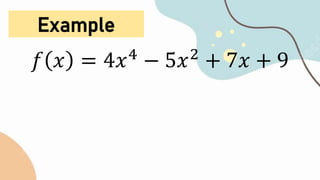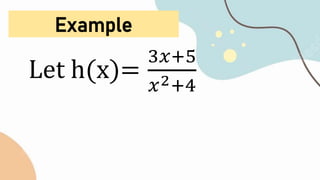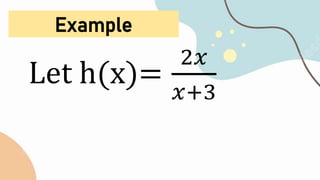The document is a prayer given at the beginning of a mathematics lesson thanking God for the opportunity to learn, asking God to enlighten their minds and give them strength to participate in the lesson, and requesting God's help to remember his glory. It then contains a summary of the key rules for differentiating algebraic functions, including the power rule, constant multiple rule, sum and difference rules, product rule, quotient rule, and chain rule, along with examples of applying each rule. The document ends with a closing prayer thanking God for being with them during the lesson and inspiring them to love and serve God.

2. Heavenly Father,
We thank you for giving us another life,
We thank you for another BeautifulDay.
As we go on through our lessons today,
May you make us instruments to do good things.
Please enlighten our minds,
Give us the strength to participatein our subject today.
Thank you for this opportunity to learn and serve others,
and help me to always remember the Truth of Your Glory!
In Jesus’ name. Amen.
O P E N I N G P R A Y E R

3. ATTENDANC
E

4. Finding the
Derivatives of
Algebraic Functions

5. Learning Targets
Apply the differentiation rules in
computing the derivatives of
algebraic expressions

6. Let us compute the derivative of the first
function of
𝑓 𝑥 = 3𝑥2
+ 4

7. We see that computing the derivative
using the definition of even a simple
polynomial is lengthy process. What
follows next rules that will enable us to
find derivatives easily. We call them
DIFFERENTIATION RULES

8. The Constant Rule
If 𝑓 𝑥 = 𝑐 where c is a constant, then 𝑓′
𝑥 =
0. The derivative of a constant is equal to zero.
Examples:
1. If f 𝑥 = 10, then 𝑓′
𝑥 = 0
2. If h 𝑥 = − 3, then ℎ′
𝑥 = 0
3. If g 𝑥 = 5𝜋, then 𝑔′
𝑥 = 0

9. DIFFERENTIATING
POWER FUNCTIONS

10. The Power Rule
If 𝑓 𝑥 = 𝑥𝑛
where 𝑛 ∈ 𝑁, then 𝑓′
𝑥 = 𝑛𝑥𝑛−1
Examples:
If 𝑓 𝑥 = 𝑥3
, then
𝑓′
𝑥 = 3𝑥3−1

11. The Power Rule
If 𝑔′
𝑥 = 𝑥5

12. The Power Rule
If 𝑔′
𝑥 = 𝑥3
, where g(x) =
1
𝑥2

13. The Power Rule
If ℎ 𝑥 = 𝑥

14. DIFFERENTIATING
A CONSTANT TIMES
A FUNCTION

15. The Constant Multiple Rule
If f 𝑥 =
𝑘 ℎ 𝑥 where k is a
constant, then
𝑓′
𝑥 = kℎ′
(𝑥)

16. Examples
1. f(x) = 5 𝑥
3
4
2. g(x) = (4 𝑥6
)
3. 𝑓 𝑥 = 3𝑥−5
4. 𝑔 𝑥 =
1
3
3
𝑥
5. ℎ 𝑥 = − 3𝑥

17. DIFFERENTIATING SUMS
AND DIFFERENCES OF
FUNCTIONS

18. The Sum Rule
If 𝑓 𝑥 = 𝑔 𝑥 + ℎ 𝑥 where g and
h are differentiable functions, then
𝑓′
𝑥 = 𝑔′
𝑥 + ℎ′
𝑥

19. Example
𝑓 𝑥 = 4𝑥4
− 5𝑥2
+ 7𝑥 + 9

20. Example
𝑓 𝑥 = 4𝑥4
− 5𝑥2
+ 7𝑥 + 9

21. The Product Rule
If f and g are differentiable functions then
𝐷𝑥[𝑓 𝑥 𝑔 𝑥 = 𝑓 𝑥 𝑔′ 𝑥 + 𝑔(𝑥)𝑓′(𝑥)

22. Example
𝐹𝑖𝑛𝑑 𝑓′
𝑥 𝑖𝑓
𝑓 𝑥 = (3𝑥2
− 4)(𝑥2
− 3𝑥)

23. The Quotient Rule
Let f(x) and g(x) be two
differentiable functions with g(x)≠ 0
𝐷𝑥
𝑓 𝑥
𝑔 𝑥
=
𝑔 𝑥 𝑓′
𝑥 − 𝑓(𝑥)𝑔′
(𝑥)
[𝑔(𝑥)2

24. Example
Let h(x)=
3𝑥+5
𝑥2+4

25. Example
Let h(x)=
2𝑥
𝑥+3

26. Chain Rule
Chain Rule for differentiation
If the function g is differentiable at x and the function f is differentiable
at g(x), then the composite function f . G is differentiable at x, and
(𝑓 ∙ 𝑔)′
𝑥 = 𝑓′
(𝑔 𝑥 )𝑔′
(𝑥)

27. Example
𝑑
𝑑𝑥
= (𝑥3
− 3𝑥2
+ 1)−3

28. Example
𝑓(𝑥) = (4𝑥2
− 4𝑥 + 2)3

29. Example
𝑓(𝑥) = (4𝑥 + 1)6

30. Dear Lord
Thank you that you promise us that when two or
more come together in Your name
You are with us.
Thank you, Lord that you have been with us
throughout this lesson.
And that you are with us right now.
Inspire us as we leave this place to love and serve
You always.
Amen.