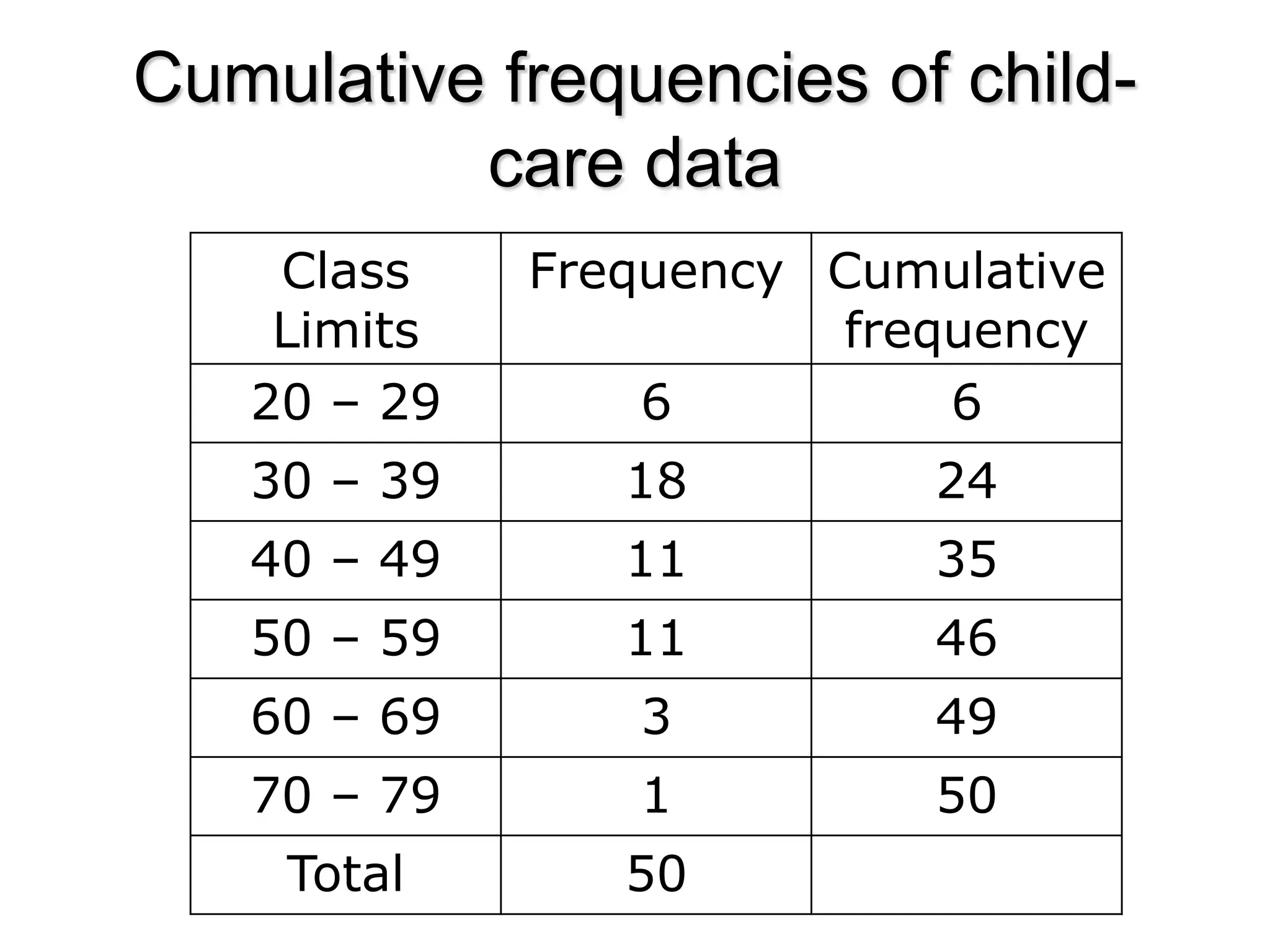
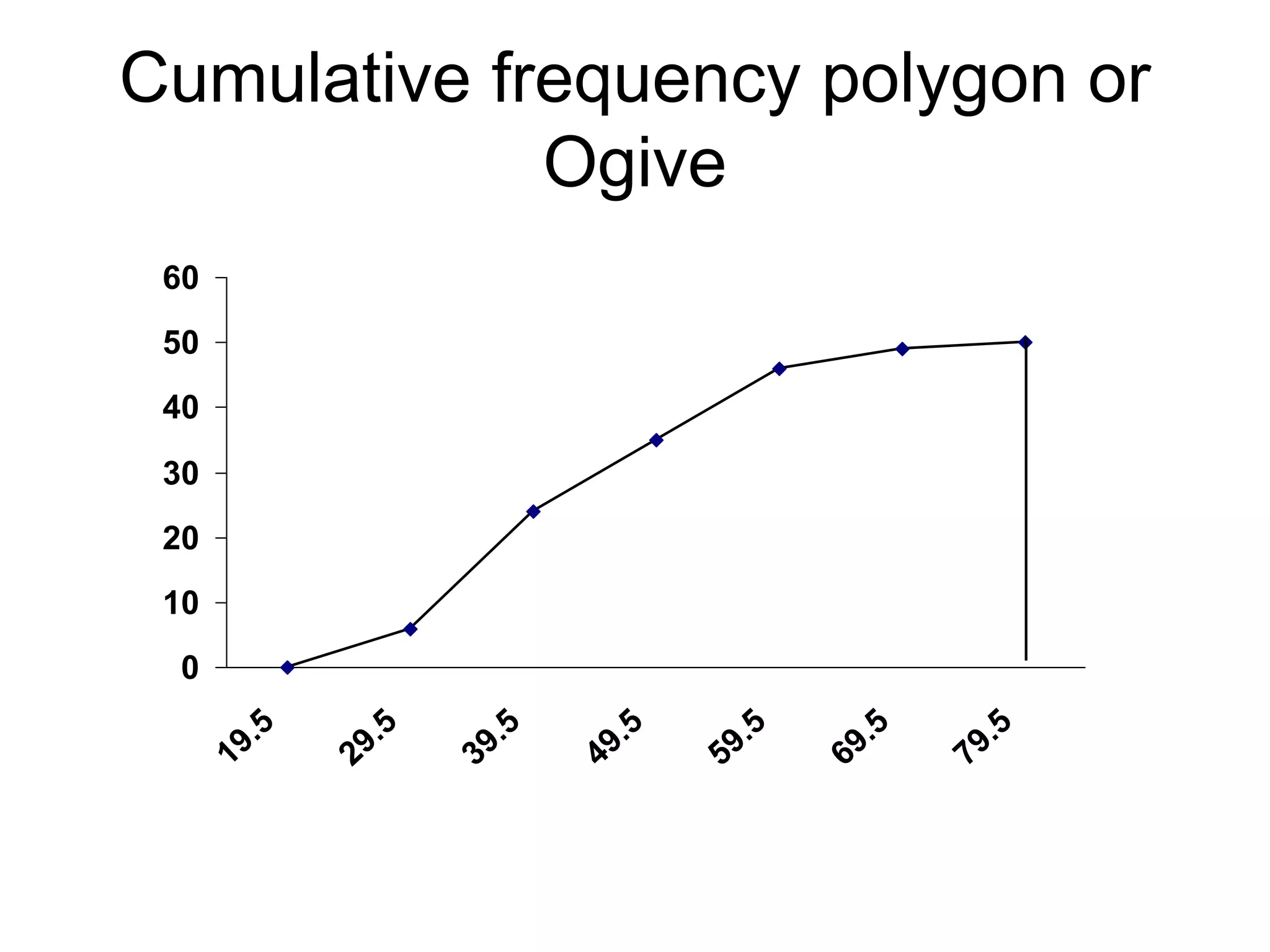
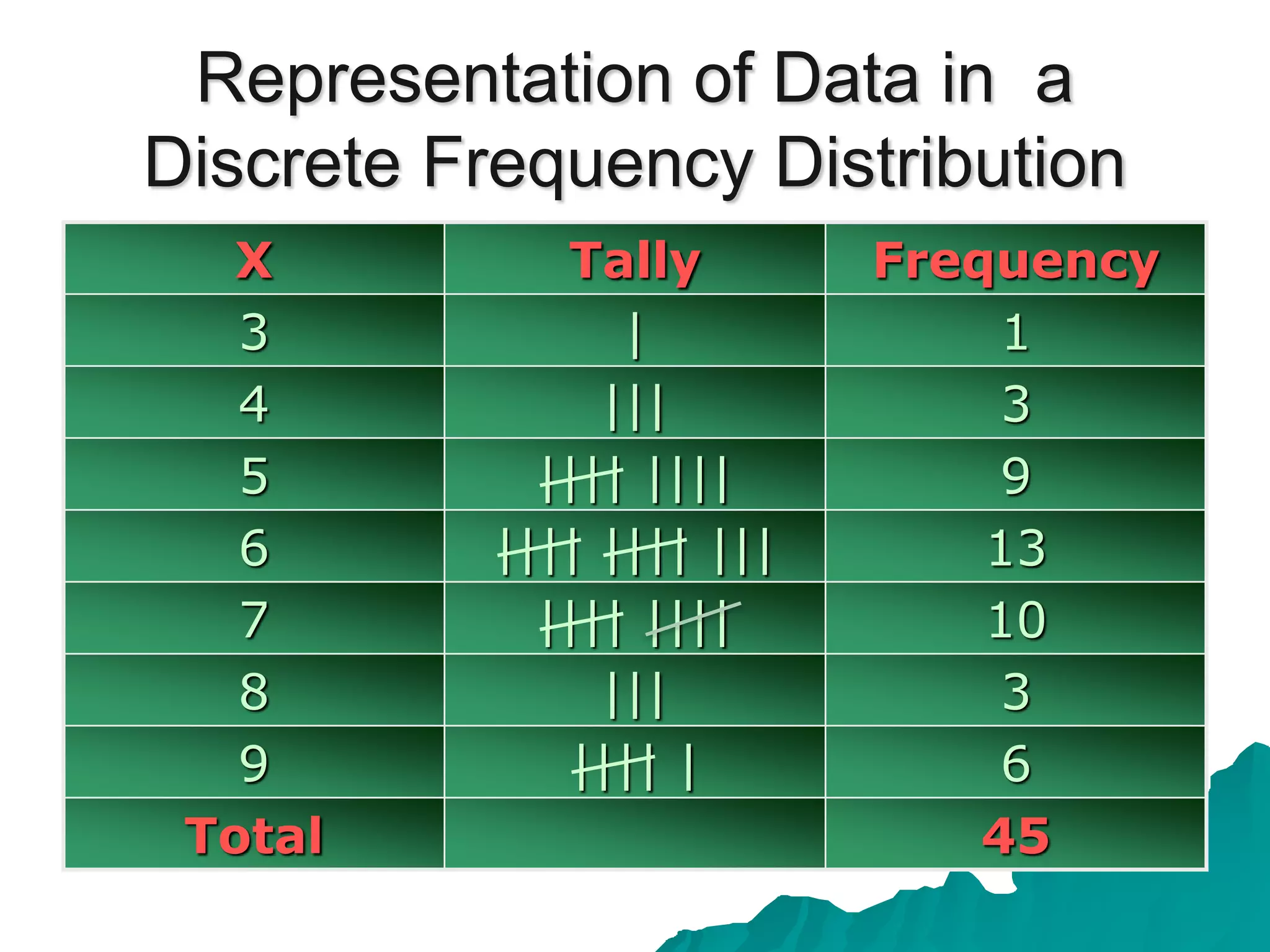
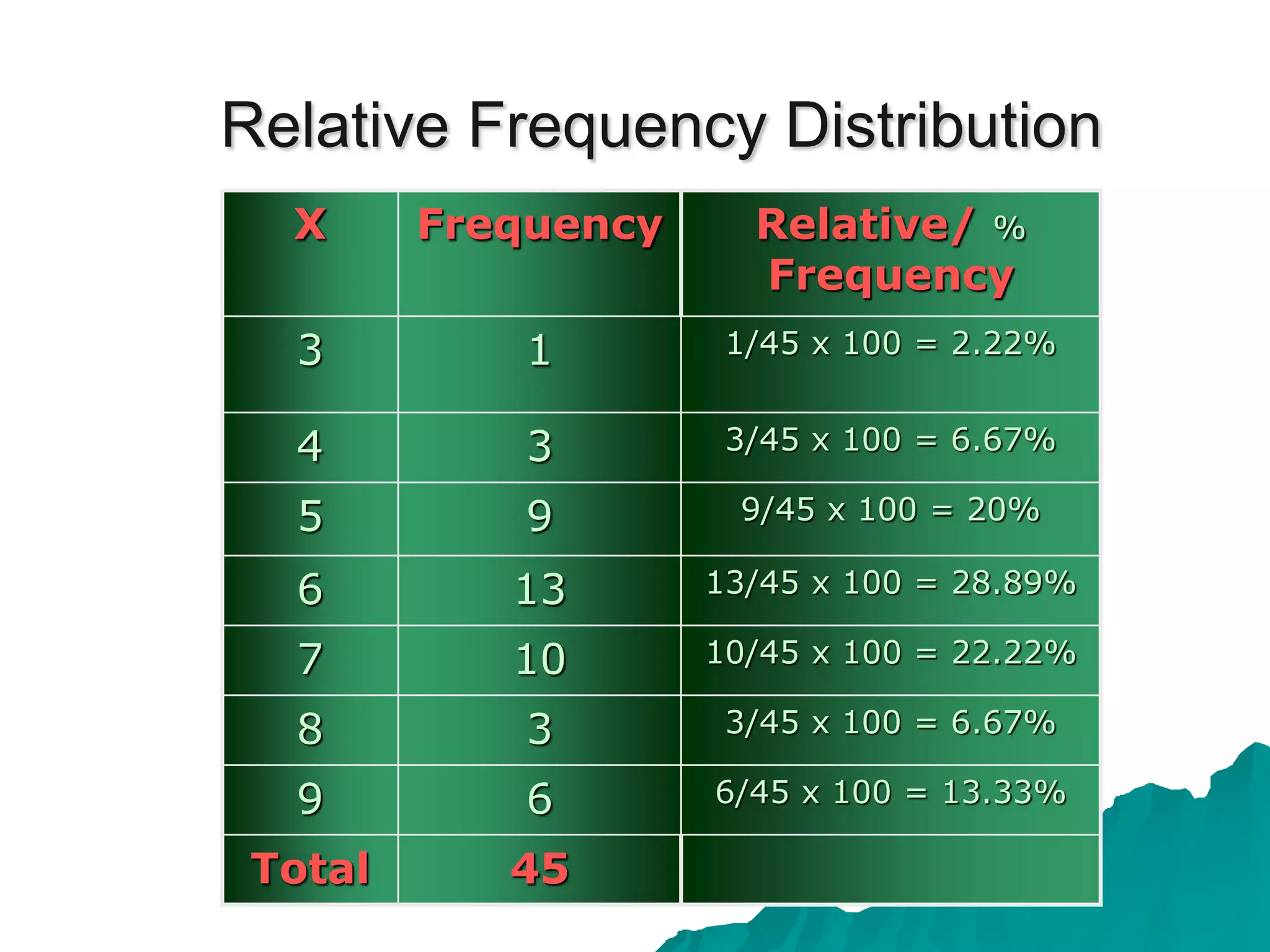
The document defines a cumulative frequency polygon (or ogive) as a graph of a cumulative frequency distribution where the upper class boundaries of a data set are plotted along the x-axis and the cumulative frequencies are plotted along the y-axis. An example is provided of age data for 50 childcare managers categorized into classes, with the corresponding frequency distribution and cumulative frequency distribution calculated and plotted on a cumulative frequency polygon.

1. The graph of a cumulative frequency
distribution is called a CUMULATIVE
FREQUENCY POLYGON or OGIVE. A
ogive is obtained by marking off the upper
class boundaries of the various classes
along the X-axis and the cumulative
frequencies along the y-axis, as shown
below:
CUMULATIVE
FREQUENCY POLYGON
or OGIVE

2. Example
The following table contains the ages
of 50 managers of child-care centers
in five cities of a developed country.
Construct the cumulative frequency
distribution and the cumulative
frequency polygon (ogive).

3. Ages of a sample of managers
of Urban child-care centers
42 26 32 34 57
30 58 37 50 30
53 40 30 47 49
50 40 32 31 40
52 28 23 35 25
30 36 32 26 50
55 30 58 64 52
49 33 43 46 32
61 31 30 40 60
74 37 29 43 54
Convert this data into Frequency Distribution.

4. Frequency Distribution of
Child-Care Managers Age
Class Limits Frequency
20 – 29 6
30 – 39 18
40 – 49 11
50 – 59 11
60 – 69 3
70 – 79 1
Total 50

5. Cumulative Frequency
The cumulative frequency is the
running total of the frequencies
through the total.
The cumulative frequency for each
class interval is the frequency for
that class interval added to the
preceding cumulative total.

6. Cumulative frequencies of child-
care data
Class
Limits
Frequency Cumulative
frequency
20 – 29 6 6
30 – 39 18 24
40 – 49 11 35
50 – 59 11 46
60 – 69 3 49
70 – 79 1 50
Total 50

7. Interpretation
 24 of the 50 managers (i.e. 48% of
the managers) are 39 years of age
or less. (i.e. less than 40 years old.)
 46 of 50 managers (i.e. 92% of the
managers) are 59 years of age or
less. (i.e. less than 60 years old.)
and so on.

8. Cumulative frequency polygon or
Ogive
0
10
20
30
40
50
60
19.5
29.5
39.5
49.5
59.5
69.5
79.5

9. Example
Suppose we walk in the nursery
class of a school and we count the no.
of Books and copies that 45 students
have in their bags.
Suppose the no. of books and copies are
9,9,3,5,4,7,6,7,5,6,5,5,8,7,5,5,6,6,6,9,6,
7,6,6,4,5,5,6, 6,6,6,7, 7,8, 5,8,8, 7, 9,
9,7, 8,7,7,9,.

10. Representation of Data in a
Discrete Frequency Distribution
X Tally Frequency
3 | 1
4 ||| 3
5 |||| |||| 9
6 |||| |||| ||| 13
7 |||| |||| 10
8 ||| 3
9 |||| | 6
Total 45

11. Graphical Representation of
Discrete Data
8
10
12
2
4
6
0 X
14
No. of books and copies
No.ofstudents

12. Relative Frequency Distribution
X Frequency Relative/ %
Frequency
3 1 1/45 x 100 = 2.22%
4 3 3/45 x 100 = 6.67%
5 9 9/45 x 100 = 20%
6 13 13/45 x 100 = 28.89%
7 10 10/45 x 100 = 22.22%
8 3 3/45 x 100 = 6.67%
9 6 6/45 x 100 = 13.33%
Total 45

13. Cumulative Frequency Distribution
X Frequency Cumulative
Frequency
3 1 1
4 3 1+3 = 4
5 9 4+9 = 13
6 13 13+13 = 26
7 10 26+10 = 36
8 3 36+3 = 39
9 6 39+6 = 45
Total 45