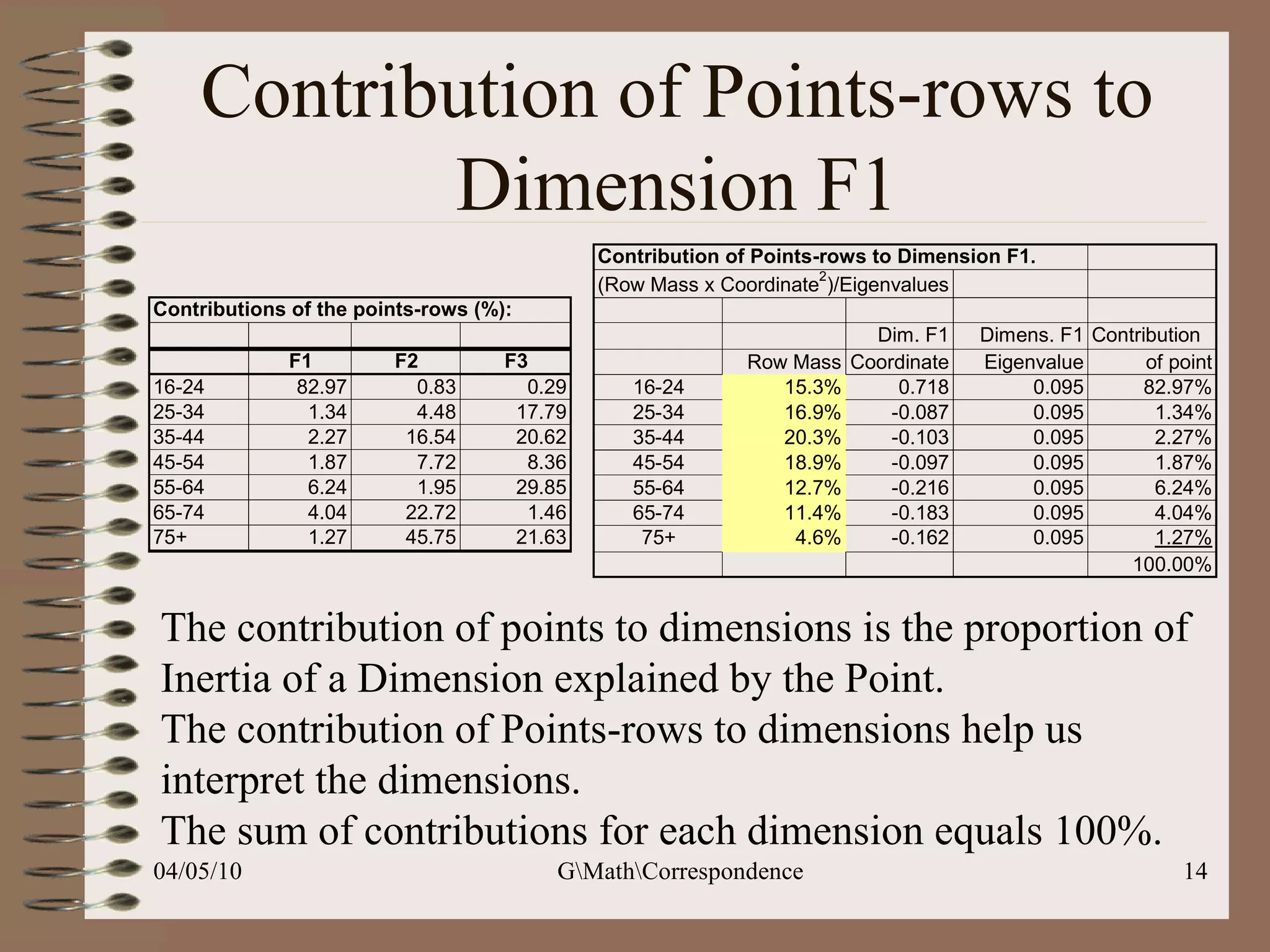
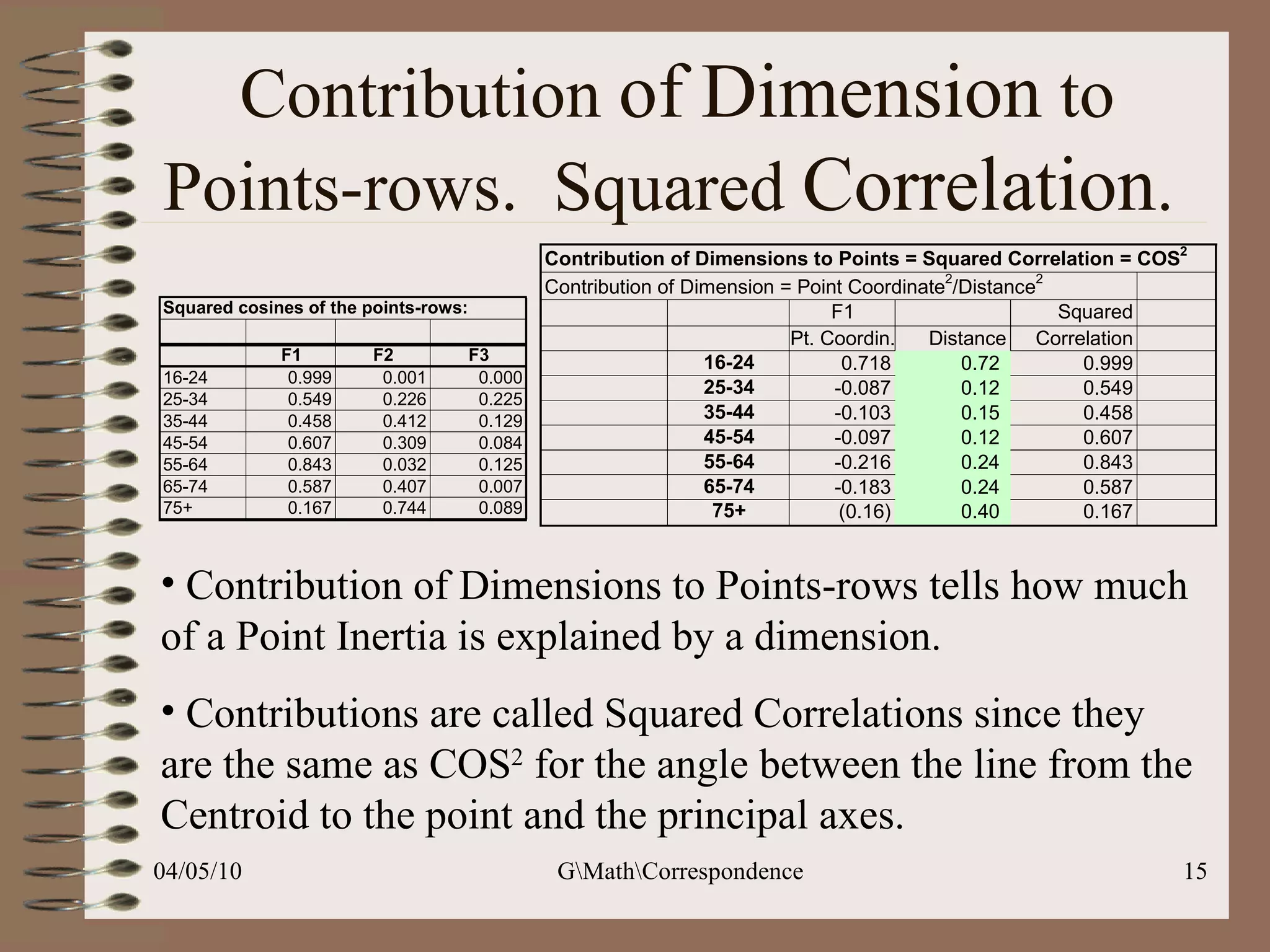
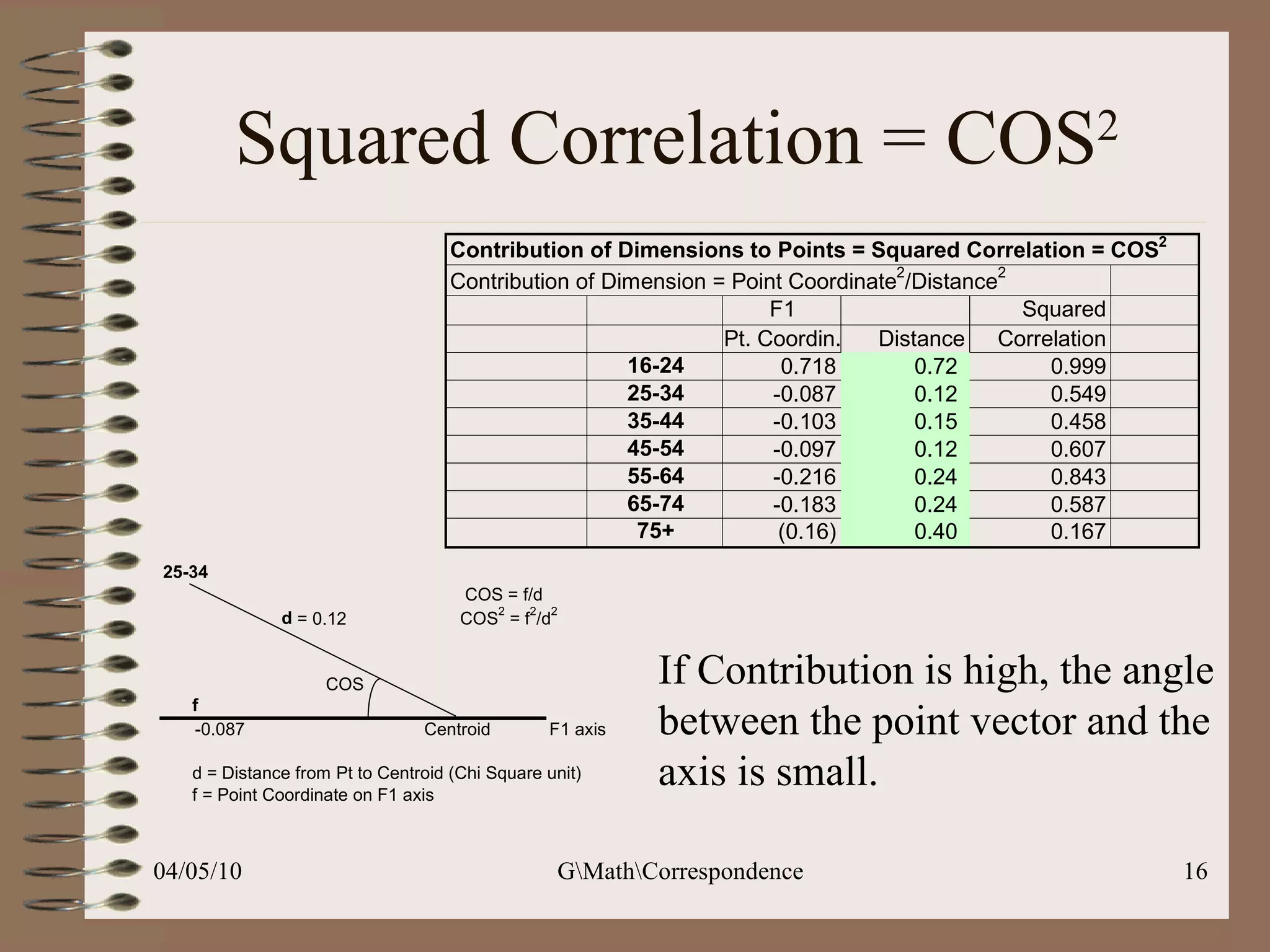
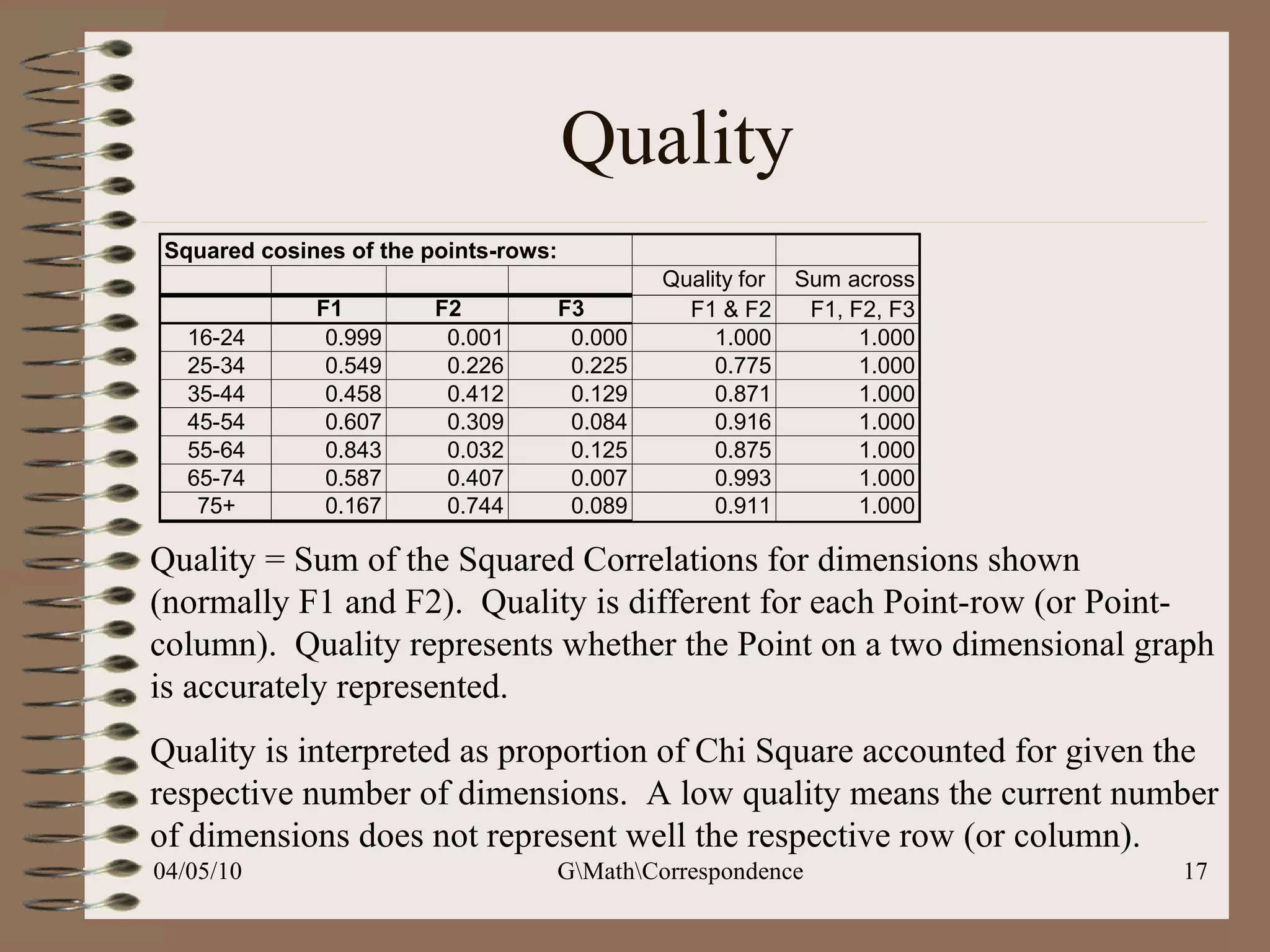
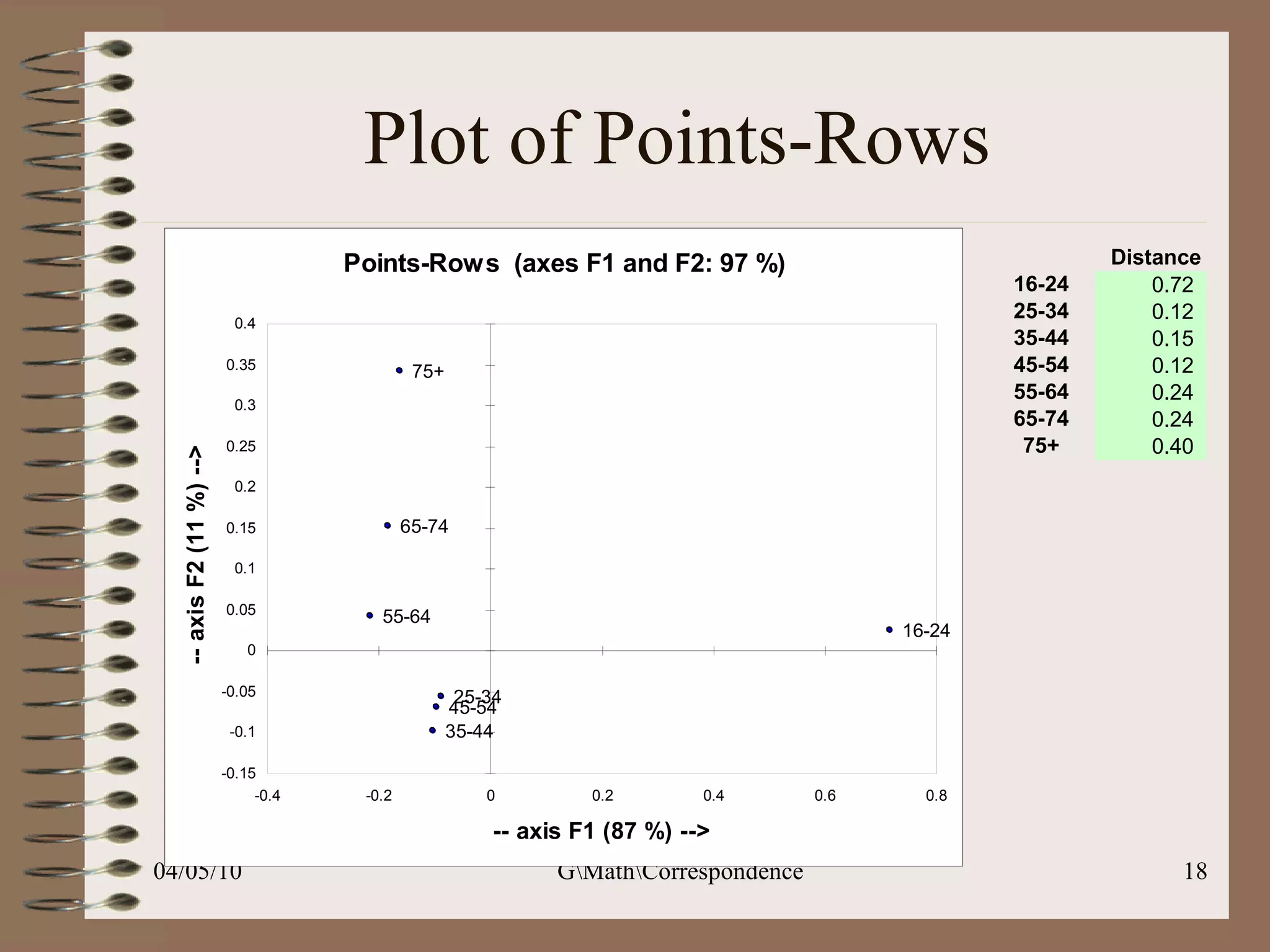
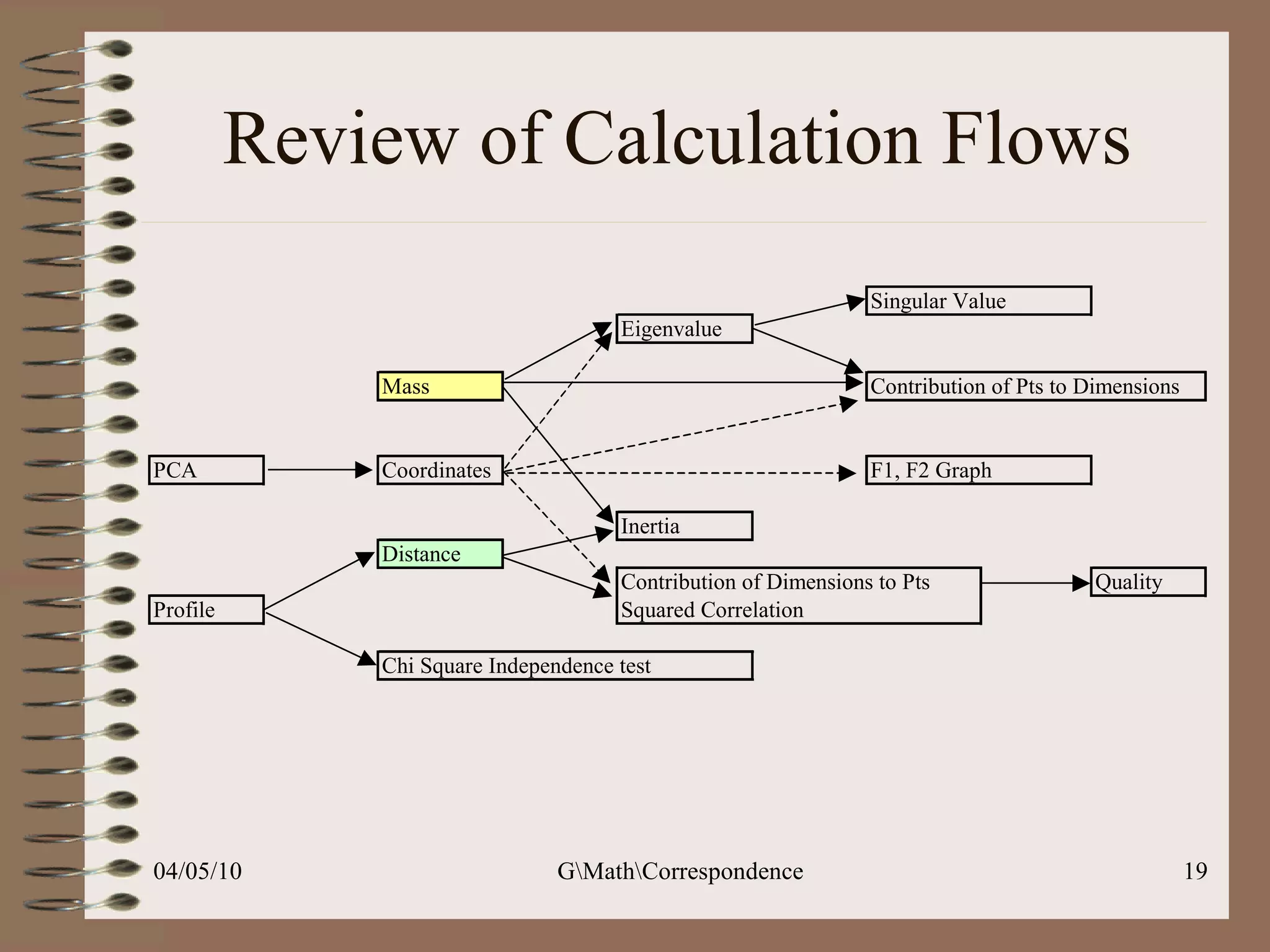
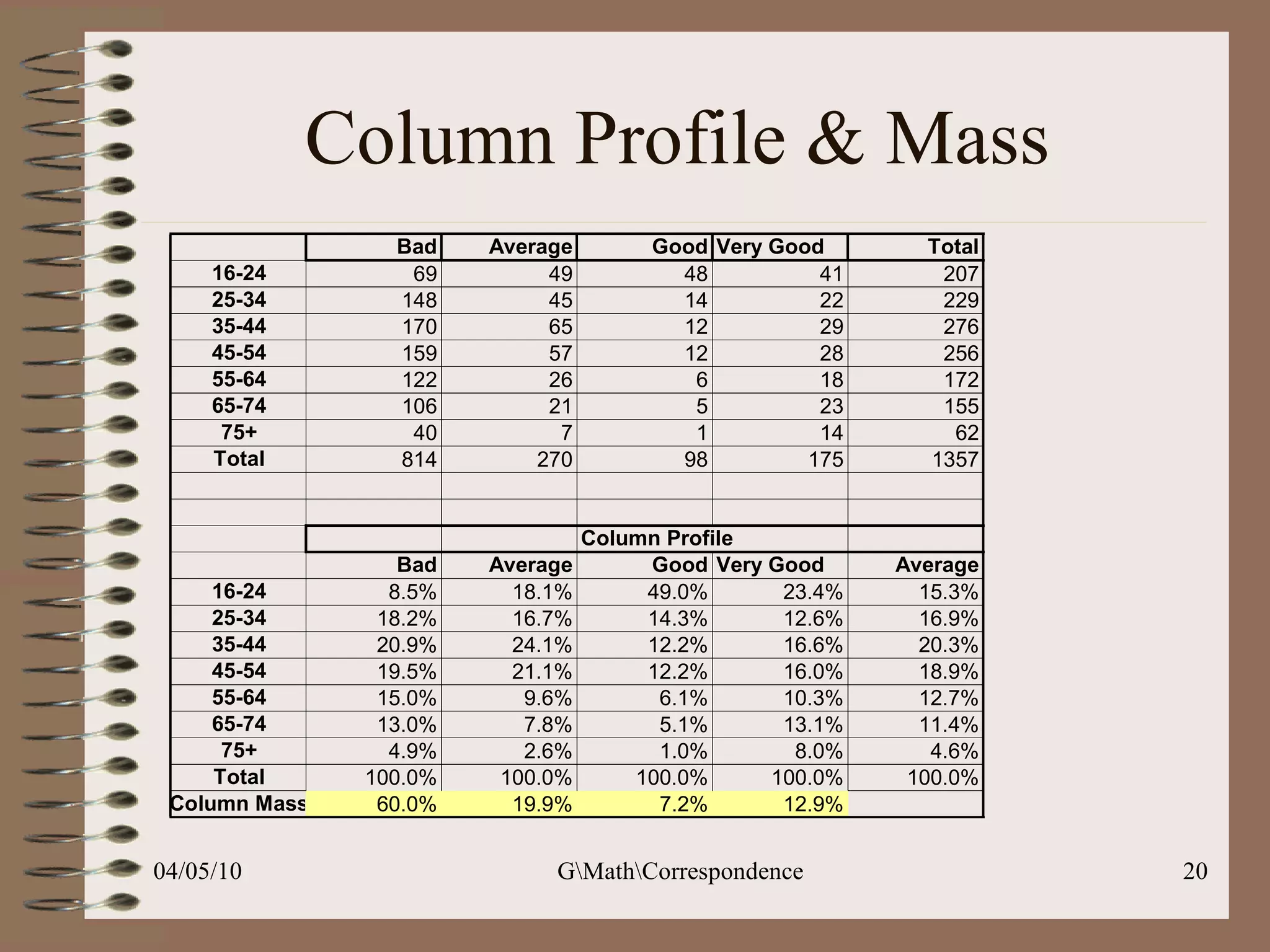
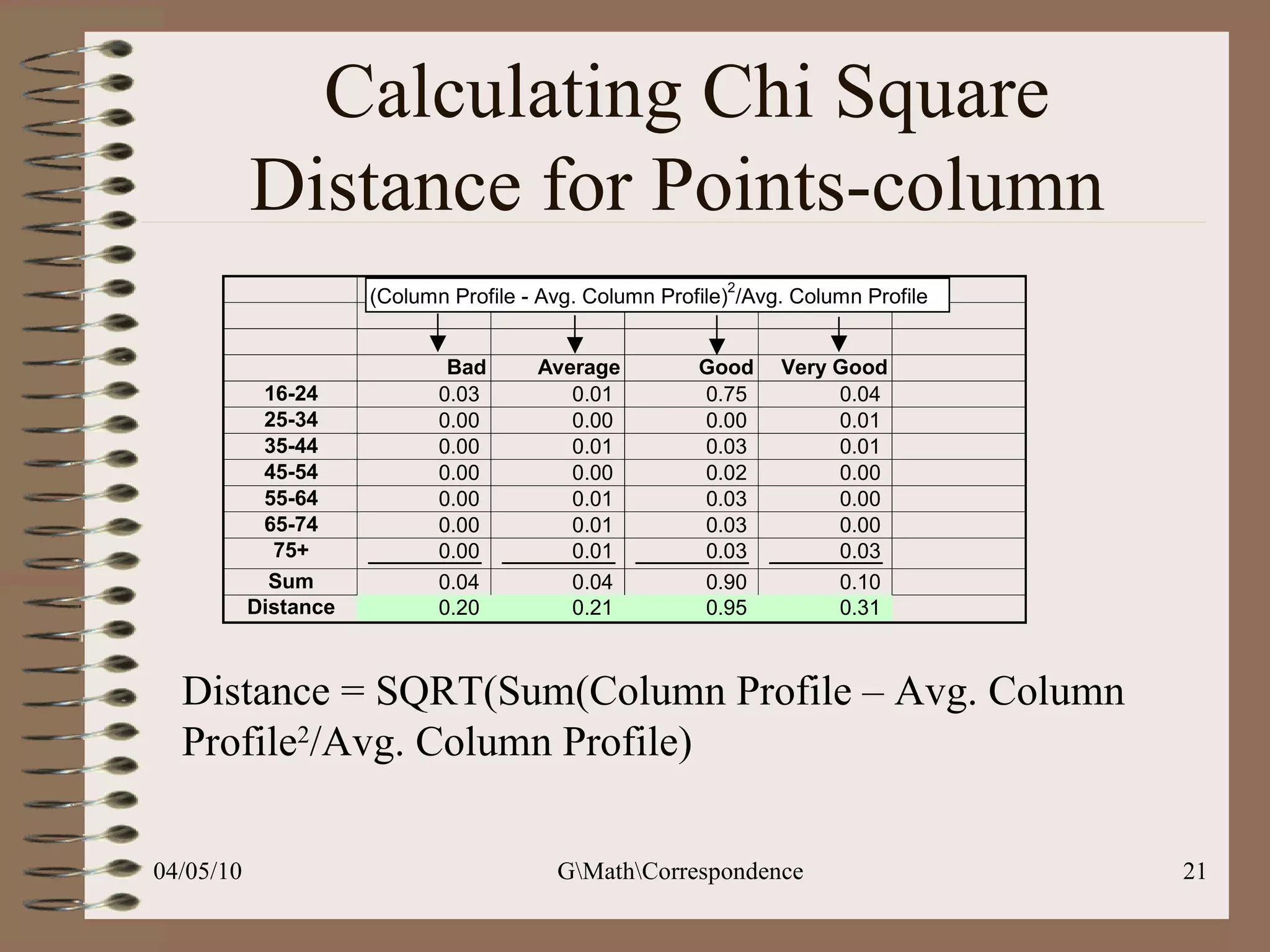
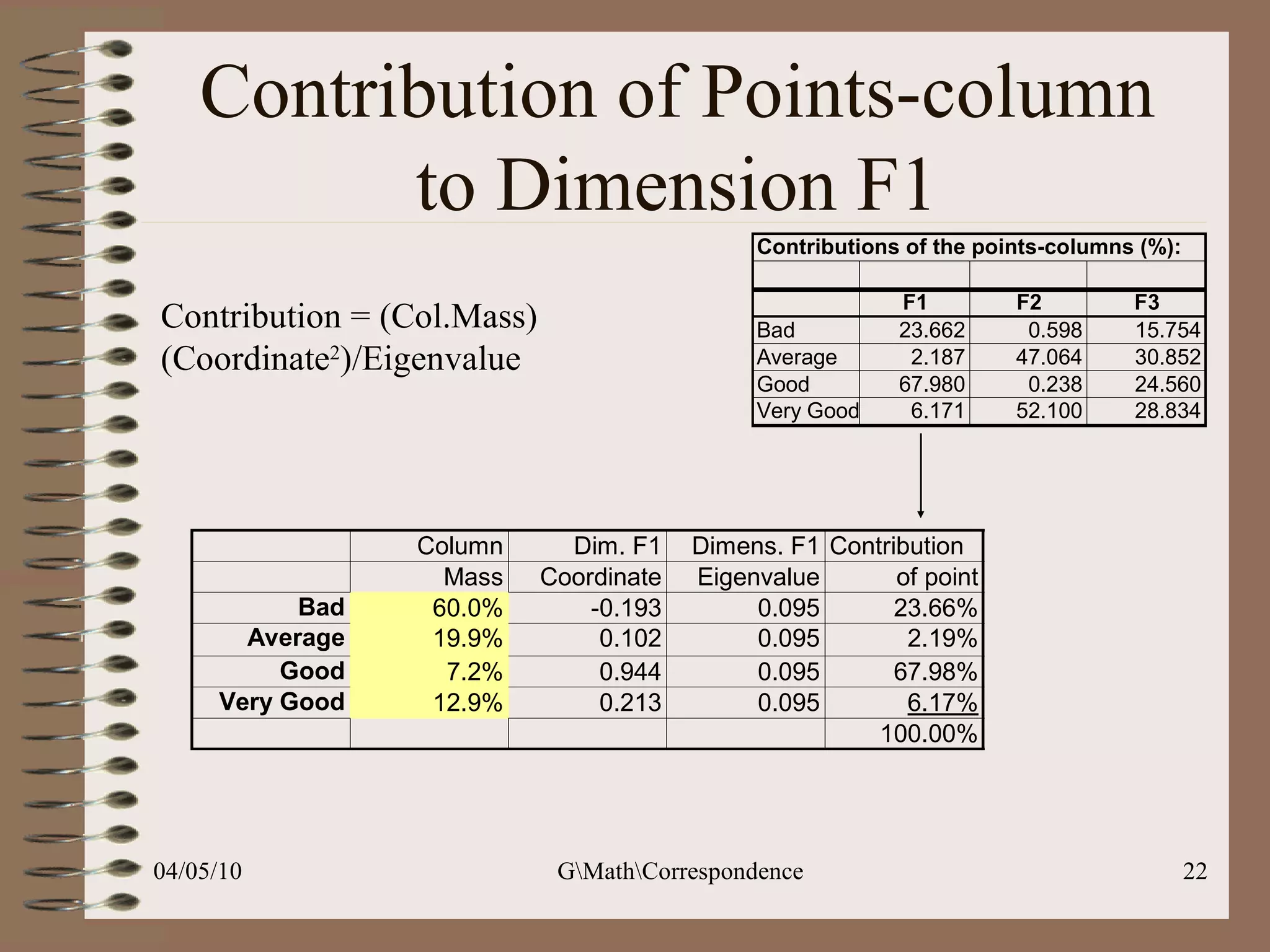
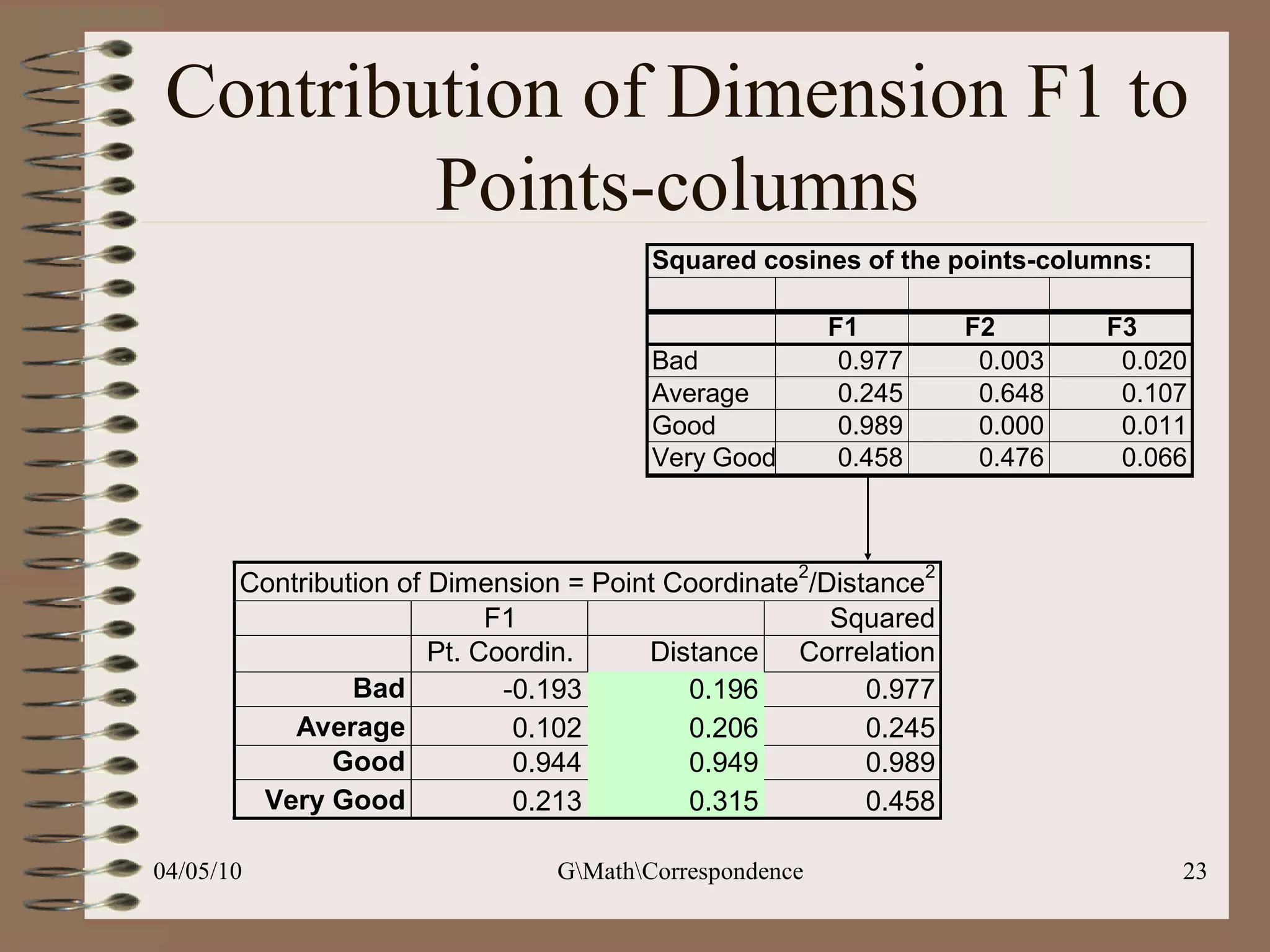
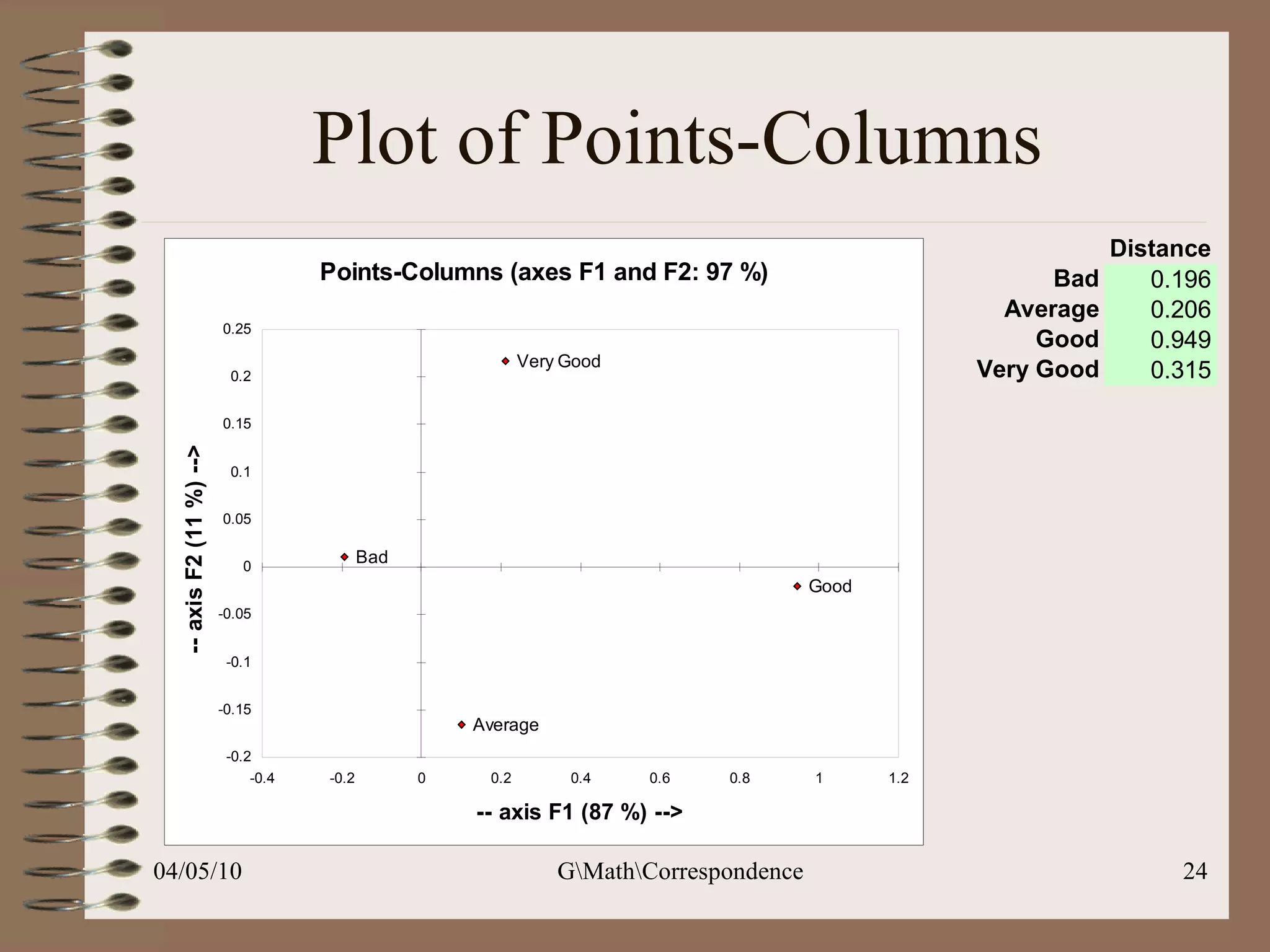
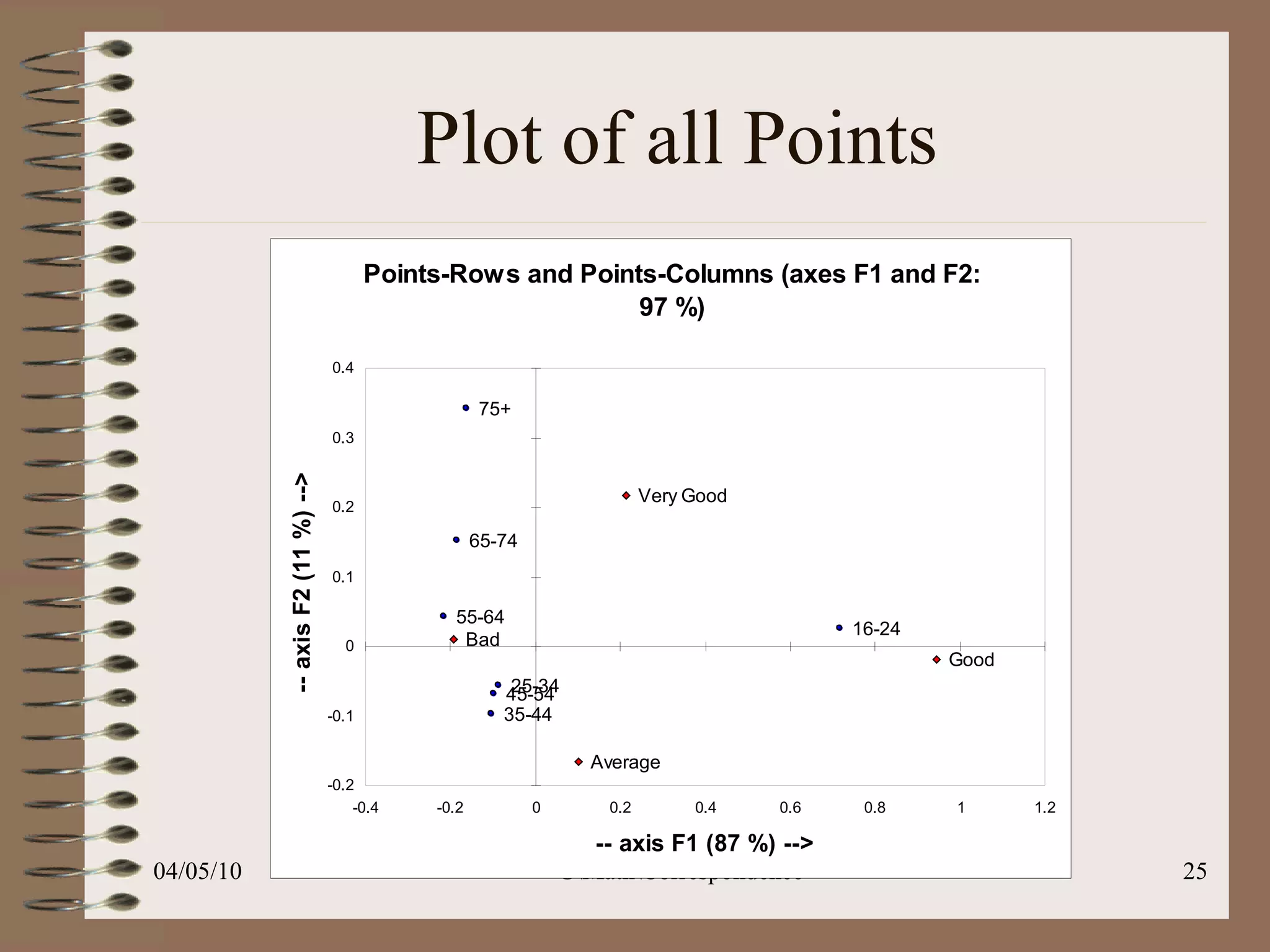
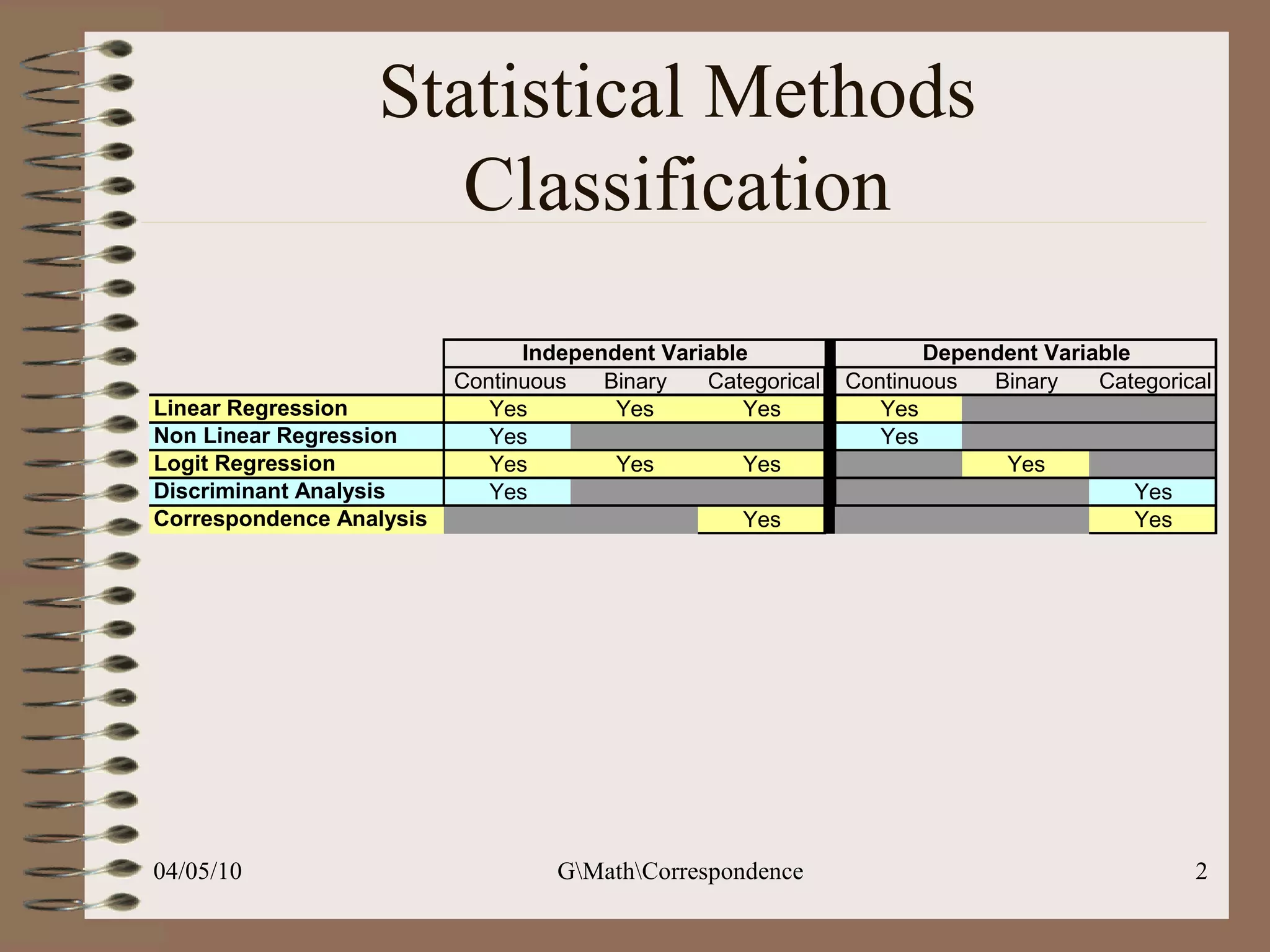
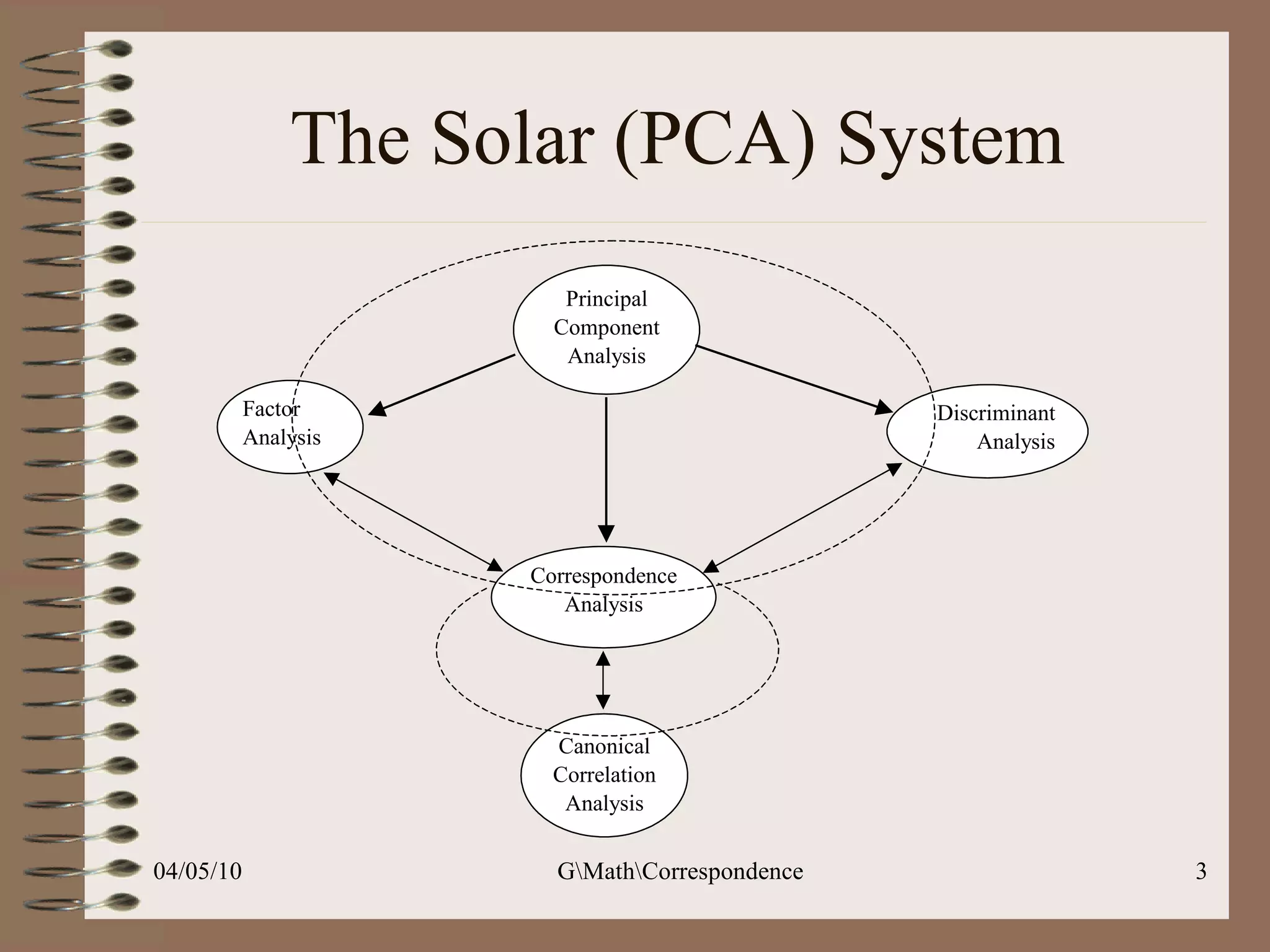
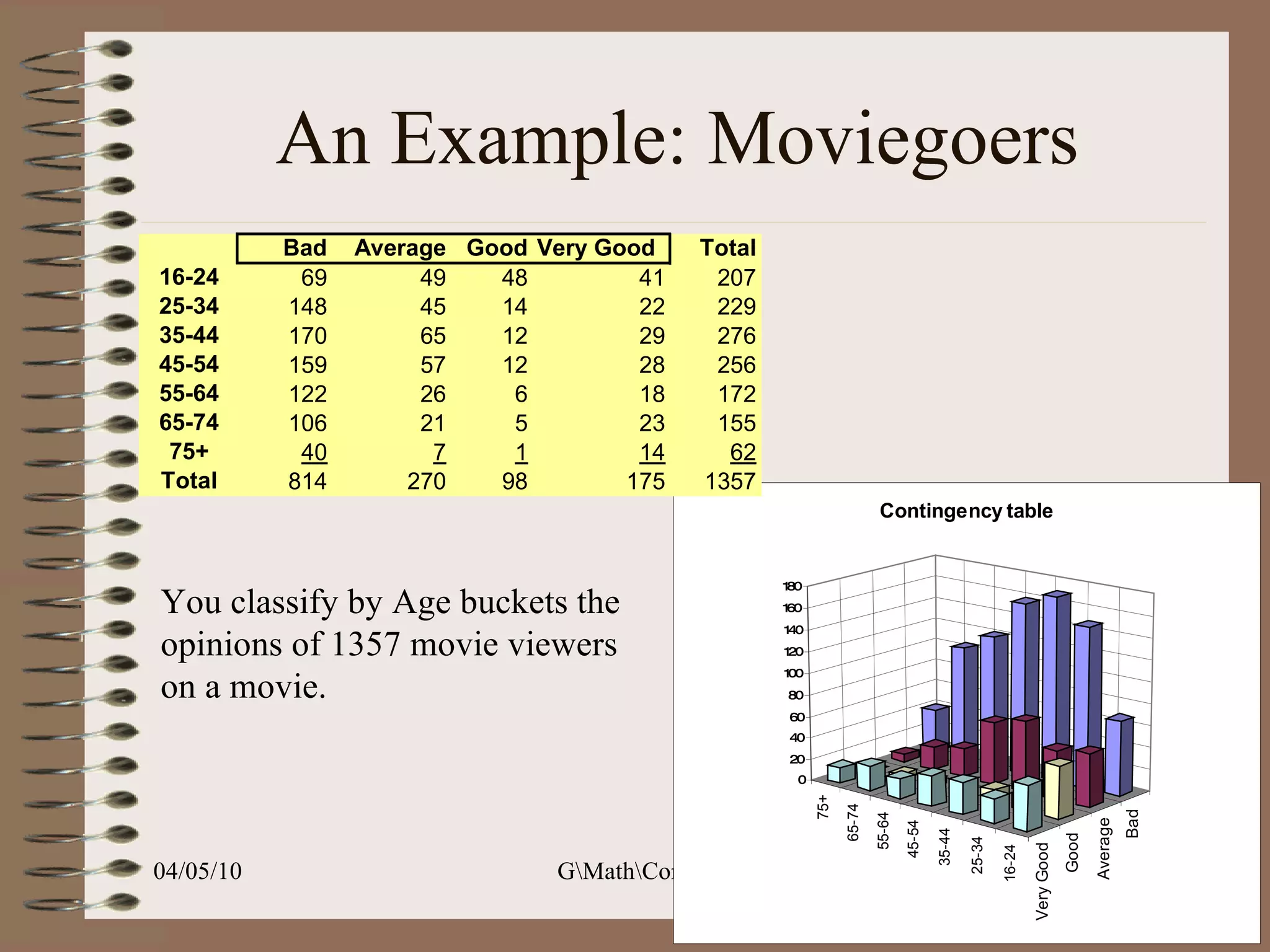
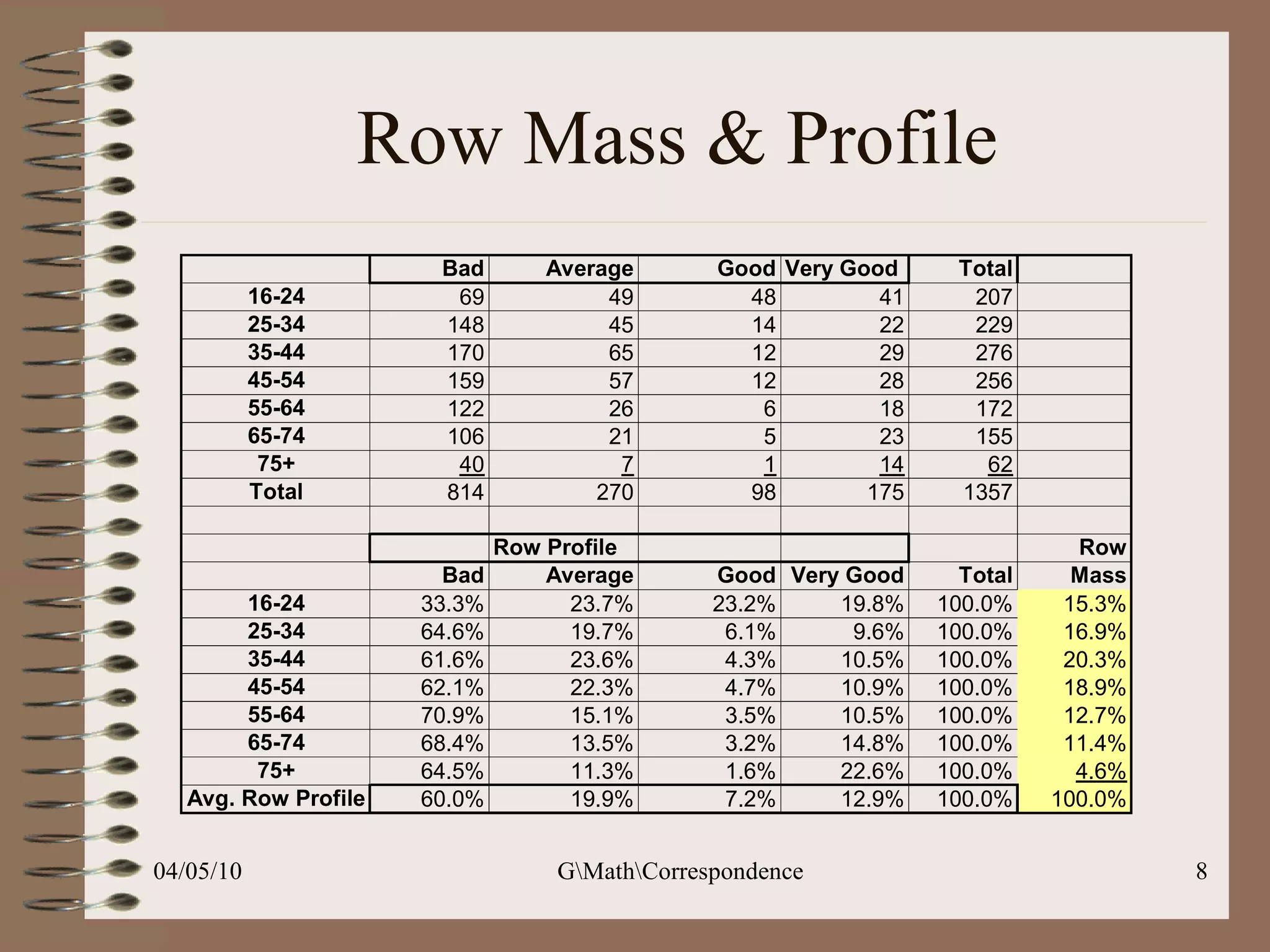
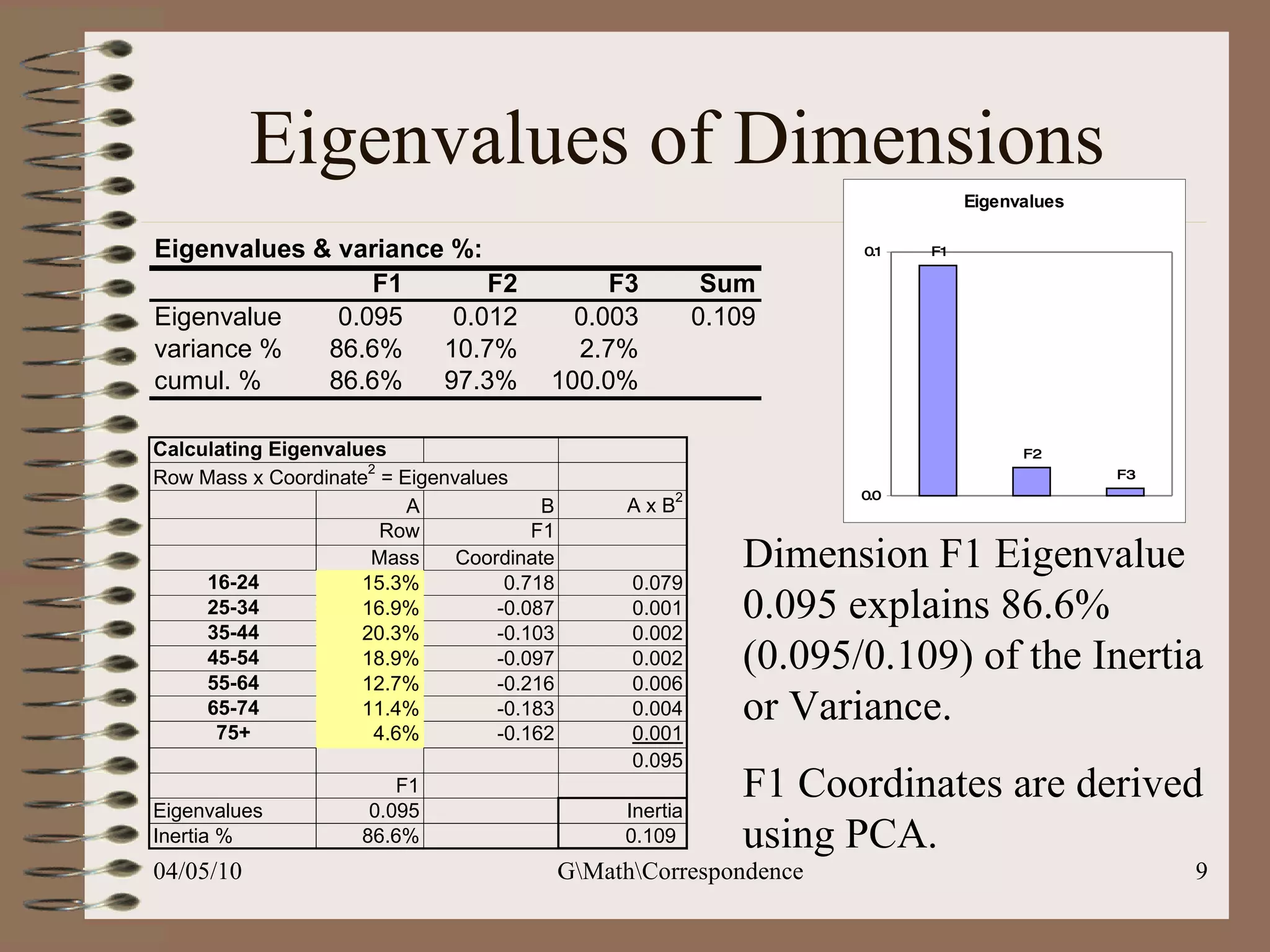
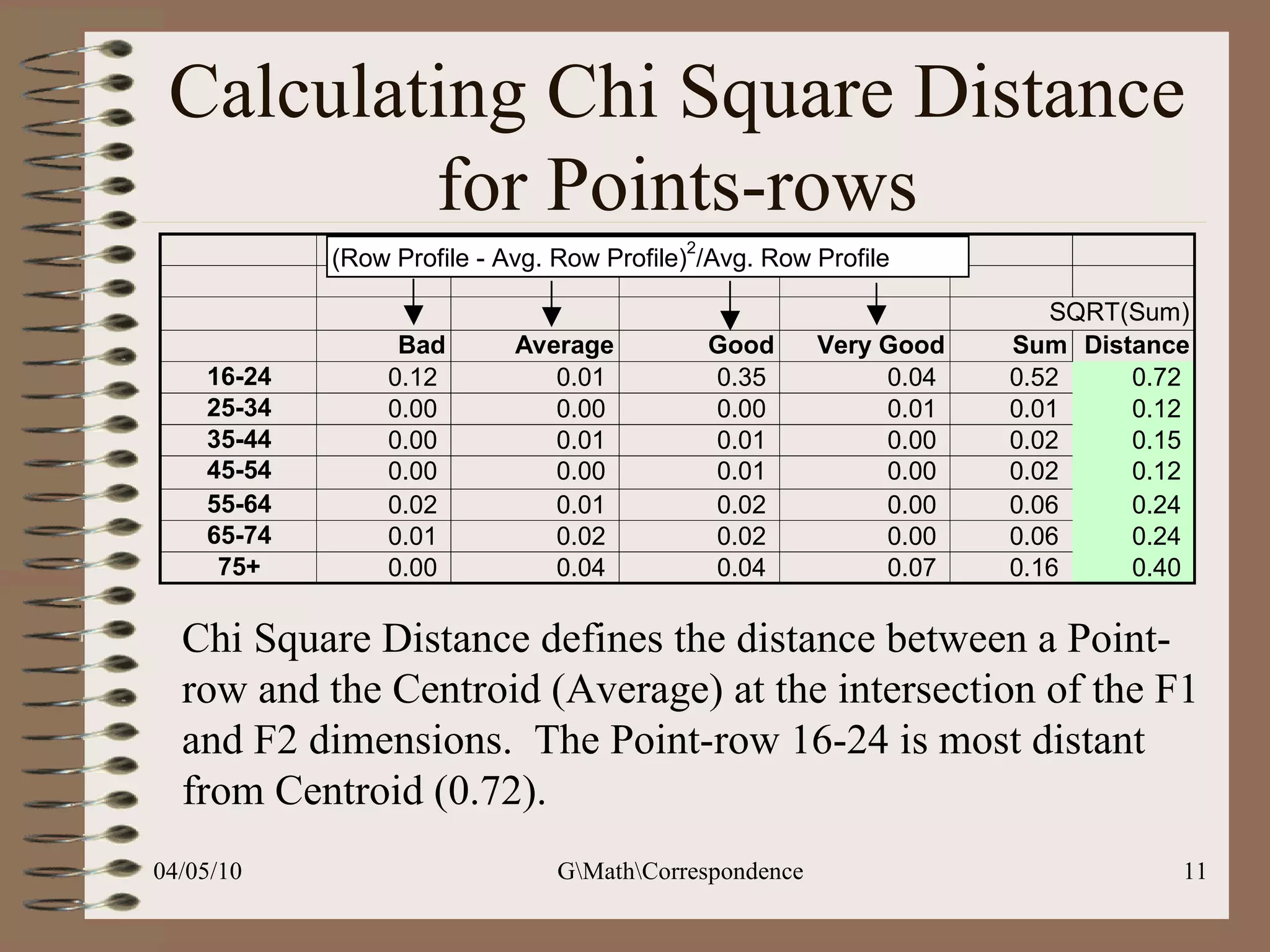
This document discusses correspondence analysis (CA), a technique that analyzes the association between two categorical variables. It provides an example of using CA to analyze the relationship between age groups and opinions on a movie from a survey of 1357 respondents. The analysis finds that the 16-24 age group and the "Good" opinion category contribute most to the variation in the data and are the most distant from the average categories. CA represents the data in a two-dimensional space to visualize these relationships between the categorical variables.

1. Correspondence Analysis with XLStat Guy Lion Financial Modeling April 2005

2. Statistical Methods Classification

3. The Solar (PCA) System

6. An Example: Moviegoers You classify by Age buckets the opinions of 1357 movie viewers on a movie.

7. Testing Independence: Chi Square One cell (16-24/Good) accounts for 49.3% (73.1/148.3) of the Chi Square value for all 28 cells. Observed Expected Bad Average Good Very Good Total Bad Average Good Very Good Total 16-24 69 49 48 41 207 16-24 124.2 41.2 14.9 26.7 207 25-34 148 45 14 22 229 25-34 137.4 45.6 16.5 29.5 229 35-44 170 65 12 29 276 35-44 165.6 54.9 19.9 35.6 276 45-54 159 57 12 28 256 45-54 153.6 50.9 18.5 33.0 256 55-64 122 26 6 18 172 55-64 103.2 34.2 12.4 22.2 172 65-74 106 21 5 23 155 65-74 93.0 30.8 11.2 20.0 155 75+ 40 7 1 14 62 75+ 37.2 12.3 4.5 8.0 62 Total 814 270 98 175 1357 Total 814 270 98 175 1357 60% 20% 7% 13% 100% 60% 20% 7% 13% 100% Chi Square Calculations (Observed - Expected) 2 /Expected Bad Average Good Very Good Total (48 - 14.9) 2 /14.9 = 73.1 16-24 24.5 1.5 73.1 7.7 106.7 25-34 0.8 0.0 0.4 1.9 3.1 35-44 0.1 1.9 3.2 1.2 6.3 45-54 0.2 0.7 2.3 0.8 4.0 55-64 3.4 2.0 3.3 0.8 9.5 Chi Squ. 148.3 65-74 1.8 3.1 3.4 0.5 8.8 DF 18 = (7 -1)(4 - 1) 75+ 0.2 2.3 2.7 4.5 9.7 p value 1.613E-22 31.1 11.5 88.3 17.3 148.3

8. Row Mass & Profile

9. Eigenvalues of Dimensions Dimension F1 Eigenvalue 0.095 explains 86.6% (0.095/0.109) of the Inertia or Variance. F1 Coordinates are derived using PCA.

10. Singular Value Singular value = SQRT(Eigenvalue). It is the maximum Canonical Correlation between the categories of the variables in analysis for any given dimension.

11. Calculating Chi Square Distance for Points-rows Chi Square Distance defines the distance between a Point-row and the Centroid (Average) at the intersection of the F1 and F2 dimensions. The Point-row 16-24 is most distant from Centroid (0.72).

12. Calculating Inertia [or Variance] using Points-rows XLStat calculates this table. It shows what Row category generates the most Inertia (Row 16-24 accounts for 72% of it)

14. Contribution of Points-rows to Dimension F1 The contribution of points to dimensions is the proportion of Inertia of a Dimension explained by the Point. The contribution of Points-rows to dimensions help us interpret the dimensions. The sum of contributions for each dimension equals 100%.

16. Squared Correlation = COS 2 If Contribution is high, the angle between the point vector and the axis is small.

17. Quality Quality = Sum of the Squared Correlations for dimensions shown (normally F1 and F2). Quality is different for each Point-row (or Point-column). Quality represents whether the Point on a two dimensional graph is accurately represented. Quality is interpreted as proportion of Chi Square accounted for given the respective number of dimensions. A low quality means the current number of dimensions does not represent well the respective row (or column).

18. Plot of Points-Rows

19. Review of Calculation Flows

20. Column Profile & Mass

21. Calculating Chi Square Distance for Points-column Distance = SQRT(Sum(Column Profile – Avg. Column Profile 2 /Avg. Column Profile)

22. Contribution of Points-column to Dimension F1 Contribution = (Col.Mass)(Coordinate 2 )/Eigenvalue

23. Contribution of Dimension F1 to Points-columns

24. Plot of Points-Columns

25. Plot of all Points

26. Observing the Correspondences

28. Conclusion (continued) We have to remember that we can’t directly compare the Distance across categories (Row vs Column). We see that the 16-24 Point-row makes a greater contribution to Inertia and overall Chi Square vs the Good Point-column. This is because the 16-24 Point-row has a greater mass (207 occurrences vs only 98 for Good).