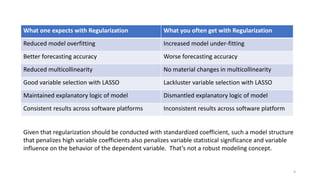
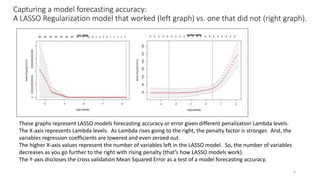
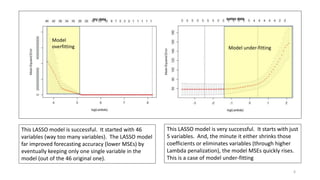
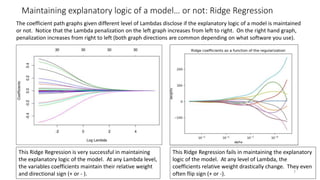
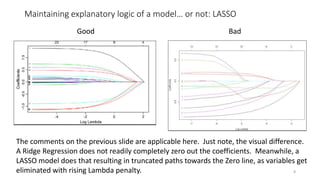
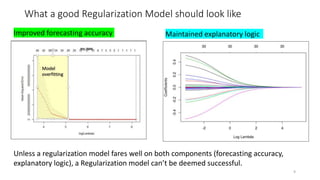
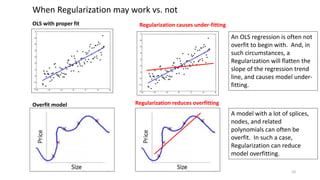
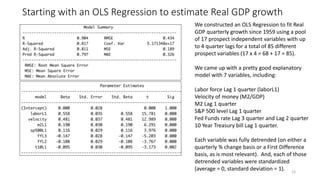
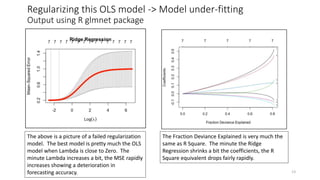
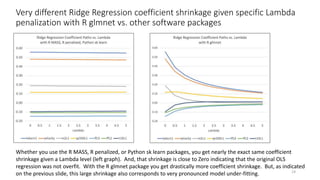
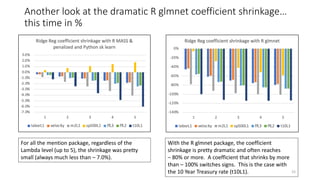
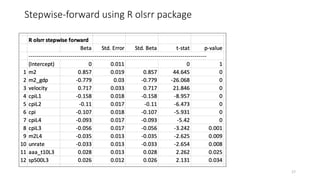
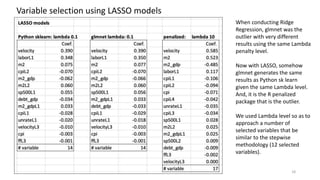
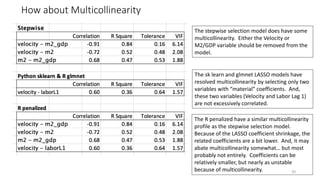
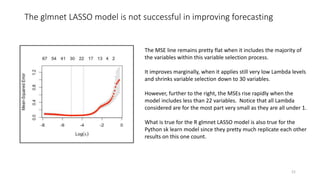
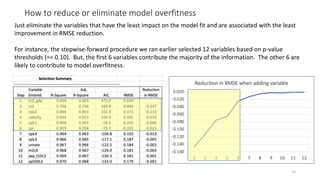
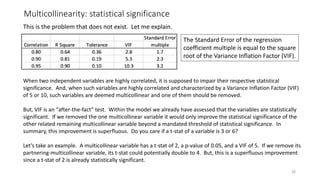
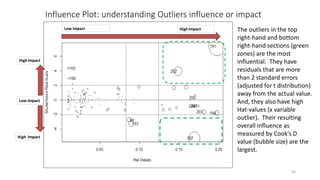
The document discusses the implications of using regularization techniques like Lasso and Ridge regression in statistical modeling, emphasizing their impact on overfitting, underfitting, and variable selection. It highlights how regularization can enhance forecasting accuracy but may compromise the explanatory logic of models by penalizing variable significance. The analysis includes practical examples and critiques of various software applications, concluding that a successful regularization model should improve both accuracy and interpretability.

1. Regularization Models
Why you should avoid them
Gaetan Lion, December 9, 2021
1

2. What is Regularization? … OLS Regression + Penalization
LASSO:
MIN[Sum of Squared Residuals + Lambda(Sum of Absolute Regression Coefficients)]
Ridge Regression:
MIN[Sum of Squared Residuals + Lambda(Sum of Squared Regression Coefficients)]
2

3. Showing the OLS term (yellow) vs. Penalization term (orange)
LASSO:
MIN[Sum of Squared Residuals + Lambda(Sum of Absolute Regression Coefficients)]
Ridge Regression:
MIN[Sum of Squared Residuals + Lambda(Sum of Squared Regression Coefficients)]
Lambda is simply a parameter, a value, or a coefficient if you will.
If Lambda = 0, the LASSO or Ridge Regression = OLS Regression
If Lambda is pretty high, the penalization is more severe. And, the variables regression
coefficients will either be zeroed out (LASSO) or very low (Ridge Regression).
3

4. 4
What one expects with Regularization What you often get with Regularization
Reduced model overfitting Increased model under-fitting
Better forecasting accuracy Worse forecasting accuracy
Reduced multicollinearity No material changes in multicollinearity
Good variable selection with LASSO Lackluster variable selection with LASSO
Maintained explanatory logic of model Dismantled explanatory logic of model
Consistent results across software platforms Inconsistent results across software platform
Given that regularization should be conducted with standardized coefficient, such a model structure
that penalizes high variable coefficients also penalizes variable statistical significance and variable
influence on the behavior of the dependent variable. That’s not a robust modeling concept.

5. Capturing a model forecasting accuracy:
A LASSO Regularization model that worked (left graph) vs. one that did not (right graph).
5
These graphs represent LASSO models forecasting accuracy or error given different penalization Lambda levels.
The X-axis represents Lambda levels. As Lambda rises going to the right, the penalty factor is stronger. And, the
variables regression coefficients are lowered and even zeroed out.
The higher X-axis values represent the number of variables left in the LASSO model. So, the number of variables
decreases as you go further to the right with rising penalty (that’s how LASSO models work).
The Y-axis discloses the cross validation Mean Squared Error as a test of a model forecasting accuracy.

6. 6
Model
overfitting Model under-fitting
This LASSO model is successful. It started with 46
variables (way too many variables). The LASSO model
far improved forecasting accuracy (lower MSEs) by
eventually keeping only one single variable in the
model (out of the 46 original one).
This LASSO model is very successful. It starts with just
5 variables. And, the minute it either shrinks those
coefficients or eliminates variables (through higher
Lambda penalization), the model MSEs quickly rises.
This is a case of model under-fitting

7. Maintaining explanatory logic of a model… or not: Ridge Regression
7
The coefficient path graphs given different level of Lambdas disclose if the explanatory logic of a model is maintained
or not. Notice that the Lambda penalization on the left graph increases from left to right. On the right hand graph,
penalization increases from right to left (both graph directions are common depending on what software you use).
This Ridge Regression is very successful in maintaining
the explanatory logic of the model. At any Lambda level,
the variables coefficients maintain their relative weight
and directional sign (+ or - ).
This Ridge Regression fails in maintaining the explanatory
logic of the model. At any level of Lambda, the
coefficients relative weight drastically change. They even
often flip sign (+ or -).

8. Maintaining explanatory logic of a model… or not: LASSO
8
Good Bad
The comments on the previous slide are applicable here. Just note, the visual difference.
A Ridge Regression does not readily completely zero out the coefficients. Meanwhile, a
LASSO model does that resulting in truncated paths towards the Zero line, as variables get
eliminated with rising Lambda penalty.

9. What a good Regularization Model should look like
9
Improved forecasting accuracy Maintained explanatory logic
Unless a regularization model fares well on both components (forecasting accuracy,
explanatory logic), a Regularization model can’t be deemed successful.

10. 10
When Regularization may work vs. not
OLS with proper fit Regularization causes under-fitting
Overfit model Regularization reduces overfitting
A model with a lot of splices,
nodes, and related
polynomials can often be
overfit. In such a case,
Regularization can reduce
model overfitting.
An OLS regression is often not
overfit to begin with. And, in
such circumstances, a
Regularization will flatten the
slope of the regression trend
line, and causes model under-
fitting.

11. Doing a specific Ridge Regression example
11

12. Starting with an OLS Regression to estimate Real GDP growth
12
We constructed an OLS Regression to fit Real
GDP quarterly growth since 1959 using a pool
of 17 prospect independent variables with up
to 4 quarter lags for a total of 85 different
prospect variables (17 x 4 = 68 + 17 = 85).
We came up with a pretty good explanatory
model with 7 variables, including:
Labor force Lag 1 quarter (laborL1)
Velocity of money (M2/GDP)
M2 Lag 1 quarter
S&P 500 level Lag 1 quarter
Fed Funds rate Lag 3 quarter and Lag 2 quarter
10 Year Treasury bill Lag 1 quarter.
Each variable was fully detrended (on either a
quarterly % change basis or a First Difference
basis, as is most relevant). And, each of those
detrended variables were standardized
(average = 0, standard deviation = 1).

13. Regularizing this OLS model -> Model under-fitting
Output using R glmnet package
13
The above is a picture of a failed regularization
model. The best model is pretty much the OLS
model when Lambda is close to Zero. The
minute Lambda increases a bit, the MSE rapidly
increases showing a deterioration in
forecasting accuracy.
The Fraction Deviance Explained is very much the
same as R Square. The minute the Ridge
Regression shrinks a bit the coefficients, the R
Square equivalent drops fairly rapidly.

14. Very different Ridge Regression coefficient shrinkage given specific Lambda
penalization with R glmnet vs. other software packages
14
Whether you use the R MASS, R penalized, or Python sk learn packages, you get nearly the exact same coefficient
shrinkage given a Lambda level (left graph). And, that shrinkage is close to Zero indicating that the original OLS
regression was not overfit. With the R glmnet package you get drastically more coefficient shrinkage. But, as indicated
on the previous slide, this large shrinkage also corresponds to very pronounced model under-fitting.

15. Another look at the dramatic R glmnet coefficient shrinkage…
this time in %
15
For all the mention package, regardless of the
Lambda level (up to 5), the shrinkage was pretty
small (always much less than – 7.0%).
With the R glmnet package, the coefficient
shrinkage is pretty dramatic and often reaches
– 80% or more. A coefficient that shrinks by more
than – 100% switches signs. This is the case with
the 10 Year Treasury rate (t10L1).

16. Doing variable selections with stepwise-
forward and LASSO
16
We will use the same data set of 85 prospect independent variables to
fit Real GDP growth.

17. Stepwise-forward using R olsrr package
17

18. 18
Variable selection using LASSO models
When conducting Ridge
Regression, glmnet was the
outlier with very different
results using the same Lambda
penalty level.
Now with LASSO, somehow
glmnet generates the same
results as Python sk learn
given the same Lambda level.
And, it is the R penalized
package that is the outlier.
We used Lambda level so as to
approach a number of
selected variables that be
similar to the stepwise
methodology (12 selected
variables).

19. Comparing the models based on variables’ influence or materiality
19
The LASSO models select a few more variables. But, far fewer of them are “material.” By, material we
mean an independent variable that has an absolute standardized coefficient > 0.1.
For the stepwise-forward model, 50% of the selected variables have an absolute standardized coefficient
> 0.1. For the LASSO models, with sk learn and glmnet, only 2 of them have a “material” coefficient.
With the R penalized package 5 out of 17 of them, or 29.4% have a material coefficient.
The sk learn and glmnet LASSO models are left with very little explanatory logic as their fit relies primarily
on just two variables (out of 14, the other 12 are pretty much immaterial with incredibly low coefficients).

20. How about Multicollinearity
20
The stepwise selection model does have some
multicollinearity. Either the Velocity or
M2/GDP variable should be removed from the
model.
The sk learn and glmnet LASSO models have
resolved multicollinearity by selecting only two
variables with “material” coefficients. And,
these two variables (Velocity and Labor Lag 1)
are not excessively correlated.
The R penalized have a similar multicollinearity
profile as the stepwise selection model.
Because of the LASSO coefficient shrinkage, the
related coefficients are a bit lower. And, it may
abate multicollinearity somewhat… but most
probably not entirely. Coefficients can be
relatively smaller, but nearly as unstable
because of multicollinearity.

21. The glmnet LASSO model is not successful in improving forecasting
21
The MSE line remains pretty flat when it includes the majority of
the variables within this variable selection process.
It improves marginally, when it applies still very low Lambda levels
and shrinks variable selection down to 30 variables.
However, further to the right, the MSEs rise rapidly when the
model includes less than 22 variables. Notice that all Lambda
considered are for the most part very small as they are all under 1.
What is true for the R glmnet LASSO model is also true for the
Python sk learn model since they pretty much replicate each other
results on this one count.

22. 22
The penalized LASSO model is inconsistent
As you increase Lambda from 3 to 10, coefficients get
increasingly shrunk and many get zeroed out. The resulting
number of variables selected declines from 26 when Lambda is 3
to 17 when Lambda is 10.
But, notice how some variables are newly selected when
Lambda increases. For instance:
a) ffL2 gets selected for the first time when Lambda increases to
10;
b) M2/GDP Lag 1 gets selected for the first time when Lambda
increases to 4;
c) 5 year Treasury Lag 3 gets selected for the first time when
Lambda increases to 4; and
d) Velocity Lag 3 gets selected for the first time when Lambda
increases to 10.
None of the above seem right for a LASSO regression. Variables
should not get newly selected when Lambda rises.

23. How to better resolve model specification issues not well
addressed by Regularization
23

24. How to diagnose model overfitness
24
1) Check the model Adjusted R Square that penalizes for adding variables;
2) Check the model Information Criteria (AIC, BIC) that also penalize for adding
variables;
3) Conduct cross validation. An overfit model will have a better historical fit (lower
error) than another model, but will generate larger cross validation errors.

25. How to reduce or eliminate model overfitness
25
Just eliminate the variables that have the least impact on the model fit and are associated with the least
improvement in RMSE reduction.
For instance, the stepwise-forward procedure we ran earlier selected 12 variables based on p-value
thresholds (=< 0.10). But, the first 6 variables contribute the majority of the information. The other 6 are
likely to contribute to model overfitness.

26. Multicollinearity: statistical significance
26
This is the problem that does not exist. Let me explain.
When two independent variables are highly correlated, it is supposed to impair their respective statistical
significance. And, when such variables are highly correlated and characterized by a Variance Inflation Factor (VIF)
of 5 or 10, such variables are deemed multicollinear and one of them should be removed.
But, VIF is an “after-the-fact” test. Within the model we already have assessed that the variables are statistically
significant. If we removed the one multicollinear variable it would only improve the statistical significance of the
other related remaining multicollinear variable beyond a mandated threshold of statistical significance. In
summary, this improvement is superfluous. Do you care if a t-stat of a variable is 3 or 6?
Let’s take an example. A multicollinear variable has a t-stat of 2, a p-value of 0.05, and a VIF of 5. If we remove its
partnering-multicollinear variable, its t-stat could potentially double to 4. But, this is a superfluous improvement
since a t-stat of 2 is already statistically significant.
The Standard Error of the regression
coefficient multiple is equal to the square
root of the Variance Inflation Factor (VIF).

27. Multicollinearity: coefficient instability
27
Ok, that is a far more pressing problem.
To test for that run a set of Rolling Regressions where you cut out a rolling window
of data (let’s say 5 years or 20 quarters of data) and observe how the variables
coefficients move over time.
By doing so, you will readily identify the variable coefficients that are unstable.
Coefficient instability can be caused by many different things besides
multicollinearity. It often is caused by instability (outliers) within the independent
variables. In such circumstances some instability within the variable coefficients is
deemed acceptable. However, if two variables are multicollinear and their
respective coefficients are unstable, removing one of those variables should help
the coefficient stability of the variable that remains in the model.

28. Coefficient instability… another solution: Robust Regression to outliers
28
There is a very interesting family of linear regressions that are robust to outliers.
They are helpful in reducing coefficient instability that is associated with volatility,
change of regime, and other divergent movements within the independent
variables and even within the dependent variable.
In other words, these regressions are robust to outliers of all kinds. The most
common ones will be described shortly. But, first let’s look at the different types of
outliers as diagnosed with an Influence Plot.

29. Understanding & Uncovering Outliers
29
Cook's D
(bubble size)
It measures the change
to the estimates that
results from deleting an
observation. It
combines Outlierness
on both the y- and x-
axes.
Threshold:> 4/n
Studentized
Residuals (y-axis)
Dependent variable
outliers
Large error. Unusual
dependent variable
value given independent
variable’s input.
Threshold: + or - 2. This
means an actual data
point is two standard
errors (scaled to a t
distribution) away from
the regressed line.
Hat-Leverage
(x-axis)
Independent variable outliers
Leverage measures how far an independent variable
deviates from its Mean. Threshold: >(2k + 2)/n
Influence Plot
Bubblerepresents Cook's D value

30. Influence Plot: understanding Outliers influence or impact
30
Low Impact HighImpact
Low Impact
High Impact
HighImpact
The outliers in the top
right-hand and bottom
right-hand sections (green
zones) are the most
influential. They have
residuals that are more
than 2 standard errors
(adjusted for t distribution)
away from the actual value.
And, they also have high
Hat-values (x variable
outlier). Their resulting
overall influence as
measured by Cook’s D
value (bubble size) are the
largest.

31. Robust Regression Methods
31
M-estimation. The M stands for “maximum likelihood type.” Also, called Iteratively Reweighted
Least-Squares (IRLS). The method is resistant to Y outliers (Studentized residuals) but not X outliers
(Leveraged points). This method is efficient and has a reasonably good regression fit. There is two
M-estimation version. The first one is called Huber M-estimation. The second one is M-estimation
bisquare. The bisquare version may have more continuous weighting of observations. Difference
between the two is often immaterial.
S-estimation. This method finds a line (plane or hyperplane) that minimizes a robust estimate of the
scale (why it is called S-est.) of the residuals. This method is resistant to both Y and X outliers. But,
it is less efficient.
MM-estimation. This method combines the efficiency of M-estimation with the resistance to both Y
and X outliers. It has also two versions (traditional and bisquare). Difference often not material.
L1 Quantile Regression. This method is resistant to both Y and X outliers by regressing estimates to
the Median instead of the Mean (like in OLS). Thus, regression coefficients are less affected by
outliers. It can withstand up to 29% reasonably bad data points (John Fox, 2010). Computation
relies on linear programming, and don’t always converge on a perfect solution (Median of estimates
often different from Median of actuals). Nevertheless, it is reasonably efficient.
Least trimmed squares (LTS). This method is resistant to both Y and X variable outliers. It minimizes
the sum of the square of the residuals, just like OLS, but only on little more than half of the
observations* away from the tails. However, it can be much less efficient. Also, there is no formula
for coefficient standard errors. So, variables stat. sign. is tough to evaluate.
*It is slightly more than half and is estimated at: m = n/2 + (k + 2)/2. (Source: Robust Regression in R, John Fox &
Sanford Weisberg, 2010).

32. Robust Regression Methods Summary
32
Approach Method Resistant to
Y outliers
Resistant to
X Outliers
Efficient Stable
Underweighting
outliers
M-estim. Yes No Yes Pretty stable
(Same as above) MM-estim. Yes Yes Yes Pretty stable
Minimize robust
estimate of the scale
of the residual
S-estim. Yes Yes Not very
efficient
Pretty stable
Regressing to the
Median instead of the
Mean
L1
Quantile
Regression
Yes Yes Yes Pretty stable
Truncating series,
eliminating the tails
by capturing just a
little more than half
the observations
Least
Trimmed
Squares
(LTS)
Yes Yes Most
inefficient
Most
unstable
MM-estimation and L1 Quantile Regression are among the preferred Robust Regression methods to deal with
outliers given their versatility and strengths on all dimensions.

33. Considerations
33
As reviewed, Regularization can often introduce numerous model weaknesses as
outlined on the fourth slide including:
a) Model under-fitting;
b) Poor forecasting accuracy; and
c) weakened explanatory logic.
Additionally, Regularization can be highly unstable or inconsistent across software
platforms resulting in divergent penalization levels depending on what software you use.
All the model issues that Regularization attempt to address can be resolved in more
reliable ways. Often, eliminating superfluous variables that can be readily identified (see
slide 25) will resolve most issues. You can also use Robust Regression to improve
coefficient stability.