(1) This document provides an introduction to complex numbers, including: defining complex numbers using i as the square root of -1, addition and multiplication of complex numbers, expressing complex numbers in polar form, and De Moivre's theorem. (2) De Moivre's theorem states that for a complex number r(cosθ + i sinθ) and integer n, (r(cosθ + i sinθ))n = rn(cos(nθ) + i sin(nθ)). It allows taking complex numbers to any power and finding roots of complex numbers. (3) The document provides examples of using De Moivre's theorem to find powers and roots of complex numbers in both

1. WelcomeWelcome
to theto the
Demo onDemo on
COMPLEX NUMBERSCOMPLEX NUMBERS
1

2. Consider the quadratic equation x2
+ 1 = 0.
Solving for x , gives x2
= – 1
12
−=x
1−=x
We make the following definition:
1−=i
Complex Numbers

3. 1−=i
Complex Numbers
12
−=iNote that squaring both sides
yields:
therefore
and
so
and
iiiii −=−== *1* 13 2
1)1(*)1(* 224
=−−== iii
iiiii === *1*45
1*1* 2246
−=== iiii
And so on…

4. Real Numbers
Imaginary
Numbers
Real numbers and imaginary numbers are
subsets of the set of complex numbers.
Complex Numbers

5. Definition of a Complex NumberDefinition of a Complex Number
If a and b are real numbers, the number a + bi is a
complex number, and it is said to be written in
standard form.
If b = 0, the number a + bi = a is a real number.
If a = 0, the number a + bi is called an imaginary
number.
Write the complex number in standard form
81 −+ =+= 81 i =•+ 241 i 221 i+

6. Addition and Subtraction of ComplexAddition and Subtraction of Complex
NumbersNumbers
If a + bi and c +di are two complex numbers written
in standard form, their sum and difference are
defined as follows.
i)db()ca()dic()bia( +++=+++
i)db()ca()dic()bia( −+−=+−+
Sum:
Difference:

7. Perform the subtraction and write the answer
in standard form.
( 3 + 2i ) – ( 6 + 13i )
= 3 + 2i – 6 – 13i
= –3 – 11i
=
=
( ) ( )234188 i+−−+
( ) ( )234298 ii +−•+
234238 ii −−+
4

8. Multiplying Complex NumbersMultiplying Complex Numbers
Multiplying complex numbers is similar to
multiplying polynomials and combining like terms.
Perform the operation and write the result in
standard form.( 6 – 2i )( 2 – 3i )
F O I L
12 – 18i – 4i + 6i2
12 – 22i + 6 ( -1 )
6 – 22i

9. Consider ( 3 + 2i )( 3 – 2i )
= 9 – 6i + 6i – 4i2
= 9 – 4( -1 )
= 9 + 4
= 13
This is a real number. The product of two
complex numbers can be a real number.
This concept can be used to divide complex numbers.

10. Complex Conjugates and DivisionComplex Conjugates and Division
Complex conjugates-a pair of complex numbers of
the form a + bi and a – bi where a and b are
real numbers.
( a + bi )( a – bi )
a 2
– abi + abi – b 2
i 2
a 2
– b 2
( -1 )
a 2
+ b 2
The product of a complex conjugate pair is a
positive real number.

11. To find the quotient of two complex numbers
multiply the numerator and denominator
by the conjugate of the denominator.
( )
( )dic
bia
+
+ ( )
( )
( )
( )dic
dic
dic
bia
−
−
•
+
+
=
22
2
dc
bdibciadiac
+
−+−
=
( )
22
dc
iadbcbdac
+
−++
=

12. Perform the operation and write the result in
standard form.
( )
( )i
i
21
76
−
− ( )
( )
( )
( )i
i
i
i
21
21
21
76
+
+
•
−
−
=
22
2
21
147126
+
−−+
=
iii
41
5146
+
++
=
i
5
520 i+
=
5
5
5
20 i
+= i+= 4

13. ii
i
−
−
+
4
31 ( ) ( )
( )i
i
ii
i
i
i
+
+
•
−
−•
+
=
4
4
4
31
Perform the operation and write the result
in standard form.
222
2
14
312
+
+
−
+
=
i
i
ii
116
312
1
1
+
+
−
−
+−
=
ii
ii
17
3
17
12
1 −−−= ii
17
3
17
12
1 −−−=
i
17
317
17
1217 −
−
−
= i
17
14
17
5
−=

14. Expressing Complex NumbersExpressing Complex Numbers
in Polar Formin Polar Form
Now, any Complex Number can be expressed as:
X + Y i
That number can be plotted as on ordered pair in
rectangular form like so…
6
4
2
-2
-4
-6
-5 5

15. Expressing Complex NumbersExpressing Complex Numbers
in Polar Formin Polar Form
Remember these relationships between polar and
rectangular form:
x
y
=θtan 222
ryx =+
θcosrx =θsinry =
So any complex number, X + Yi, can be written in
polar form: irrYiX θθ sincos +=+
)sin(cossincos θθθθ irirr +=+
θrcis
Here is the shorthand way of writing polar form:

16. Expressing Complex NumbersExpressing Complex Numbers
in Polar Formin Polar Form
Rewrite the following complex number in polar
form:
4 - 2i
Rewrite the following complex number in
rectangular form: 0
307cis

17. Expressing Complex NumbersExpressing Complex Numbers
in Polar Formin Polar Form
Express the following complex number in
rectangular form:
)
3
sin
3
(cos2
ππ
i+

18. Expressing Complex NumbersExpressing Complex Numbers
in Polar Formin Polar Form
Express the following complex number in
polar form: 5i

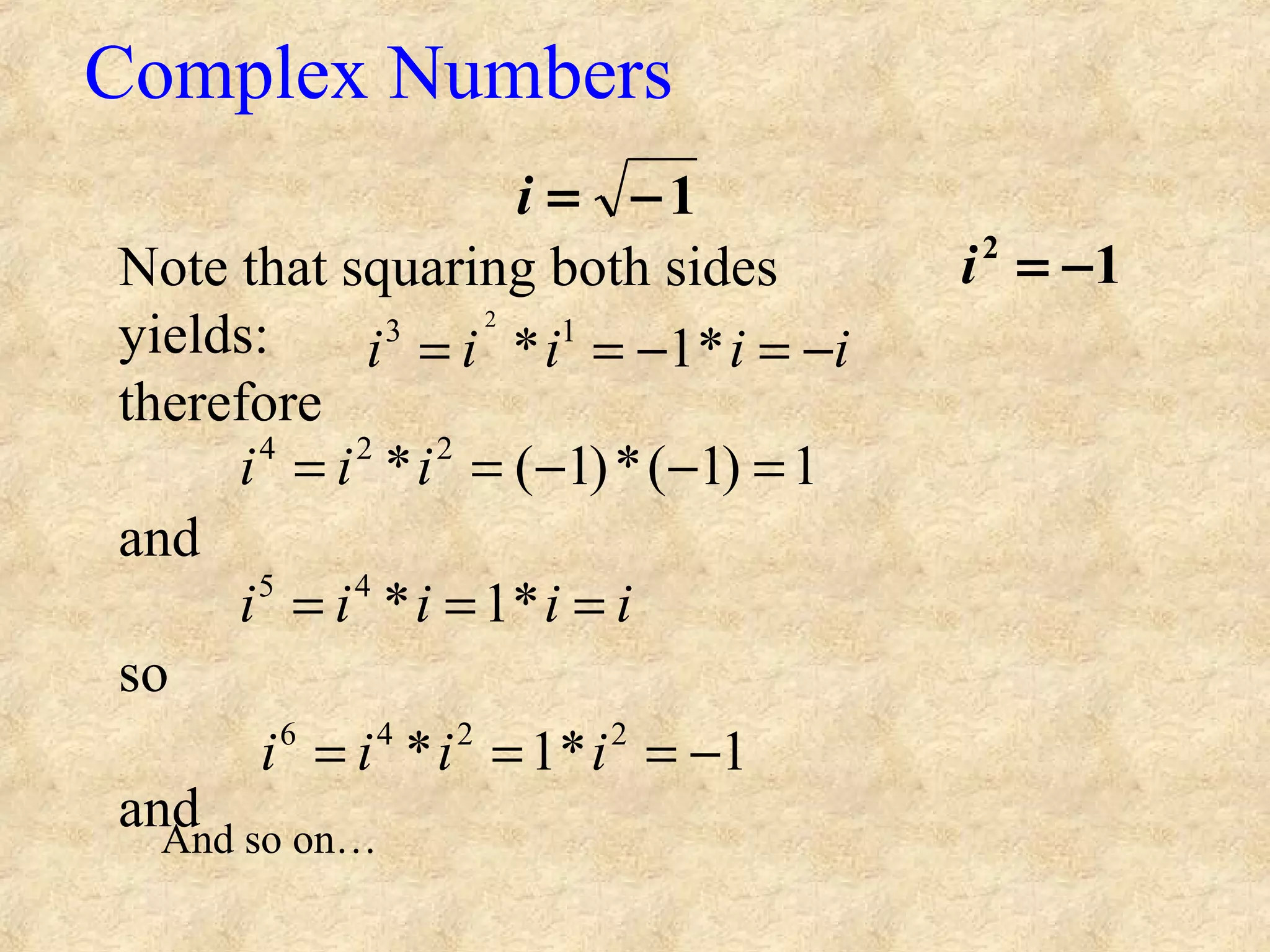
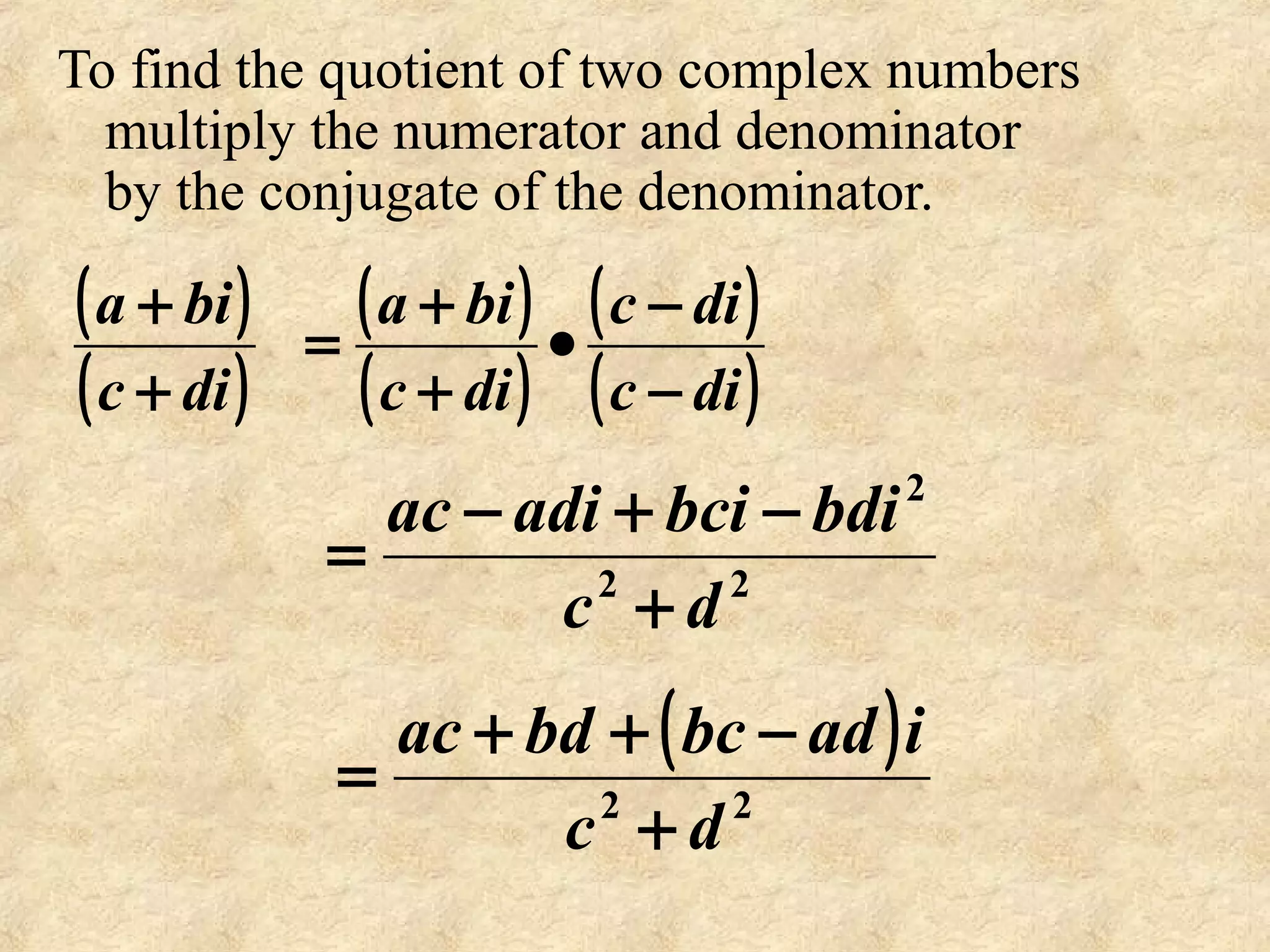
19. Products and Quotients ofProducts and Quotients of
Complex Numbers in Polar FormComplex Numbers in Polar Form
)sin(cos 111 θθ ir +
The product of two complex numbers,
and
Can be obtained by using the following formula:
)sin(cos 222 θθ ir +
)sin(cos*)sin(cos 222111 θθθθ irir ++
)]sin()[cos(* 212121 θθθθ +++= irr

20. Products and Quotients ofProducts and Quotients of
Complex Numbers in Polar FormComplex Numbers in Polar Form
)sin(cos 111 θθ ir +
The quotient of two complex numbers,
and
Can be obtained by using the following formula:
)sin(cos 222 θθ ir +
)sin(cos/)sin(cos 222111 θθθθ irir ++
)]sin()[cos(/ 212121 θθθθ −+−= irr

21. Products and Quotients ofProducts and Quotients of
Complex Numbers in Polar FormComplex Numbers in Polar Form
Find the product of 5cis30 and –2cis120
Next, write that product in rectangular form

22. Products and Quotients ofProducts and Quotients of
Complex Numbers in Polar FormComplex Numbers in Polar Form
Find the quotient of 36cis300 divided by
4cis120
Next, write that quotient in rectangular form

23. Products and Quotients ofProducts and Quotients of
Complex Numbers in Polar FormComplex Numbers in Polar Form
Find the result of
Leave your answer in polar form.
Based on how you answered this problem,
what generalization can we make about
raising a complex number in polar form to
a given power?
4
))120sin120(cos5( i+

24. De Moivre’s TheoremDe Moivre’s Theorem
De Moivre's Theorem is the theorem which
shows us how to take complex numbers to any
power easily.
De Moivre's Theorem – Let r(cos Φ+isin Φ) be a
complex number and n be any real number. Then
[r(cos Φ+isin Φ]n
= rn
(cos nΦ+isin nΦ)
What is this saying?
The resulting r value will be r to the nth
power and the
resulting angle will be n times the original angle.

25. De Moivre’s TheoremDe Moivre’s Theorem
Try a sample problem: What is [3(cos 45°+isin45)]5
?
To do this take 3 to the 5th
power, then multiply 45 times 5
and plug back into trigonometric form.
35
= 243 and 45 * 5 =225 so the result is 243(cos 225°+isin 225°)
Remember to save space you can write it in compact form.
243(cos 225°+isin 225°)=243cis 225°

26. De Moivre’s TheoremDe Moivre’s Theorem
Find the result of:
Because of the power involved, it would easier to change this
complex number into polar form and then use De Moivre’s Theorem.
4
)1( i−

27. De Moivre’s TheoremDe Moivre’s Theorem
De Moivre's Theorem also works not only for
integer values of powers, but also rational values
(so we can determine roots of complex numbers).
pp
rcisyix
11
)()( θ=+
)()
1
*(
11
p
cisr
p
cisr pp θ
θ ==

28. De Moivre’s TheoremDe Moivre’s Theorem
Simplify the following: 3
1
)344( i−

29. De Moivre’s TheoremDe Moivre’s Theorem
Every complex number has ‘p’ distinct ‘pth’ complex
roots (2 square roots, 3 cube roots, etc.)
To find the p distinct pth roots of a complex number,
we use the following form of De Moivre’s Theorem
)
360
()(
11
p
n
cisryix pp +
=+
θ
…where ‘n’ is all integer values between 0 and p-1.
Why the 360? Well, if we were to graph the complex
roots on a polar graph, we would see that the p roots
would be evenly spaced about 360 degrees (360/p would
tell us how far apart the roots would be).

30. De Moivre’s TheoremDe Moivre’s Theorem
Find the 4 distinct 4th roots of -3 - 3i

31. De Moivre’s TheoremDe Moivre’s Theorem
Solve the following equation for all complex
number solutions (roots): 0273
=+x