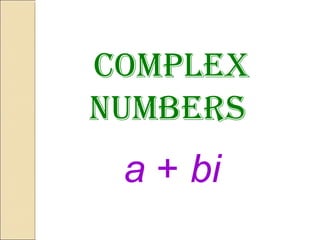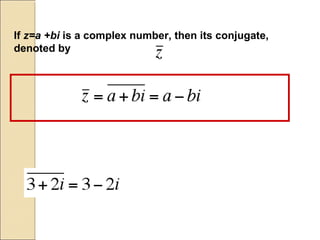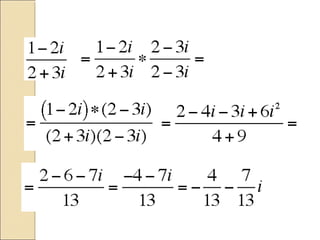The document discusses complex numbers of the form a + bi, covering their addition, subtraction, multiplication, and division. It also explains quadratic equations, including how to determine solutions using the discriminant and the quadratic formula. Through various examples, it illustrates methods for solving quadratic equations and highlights different outcomes based on the discriminant's value.

1. COMPLEX NUMBERS ANDCOMPLEX NUMBERS AND
QUADRATIC EQUATIONSQUADRATIC EQUATIONS
From: Deepanshu Chowdhary
Class: 11th
A

2. Complex
Numbers
a + bi

3. Complex numbers are numbers of the
form a + bi, where a and b are real
numbers. The real number a is called the
real part of the number a + bi; the real
number b is called the imaginary part of
a + bi.

4. (a + bi) + (c + di) = (a + c) + (b + d)i
(2 + 4i) + (-1 + 6i) = (2 - 1) + (4 + 6)i
= 1 + 10i
Sum of Complex Numbers

5. (a + bi) - (c + di) = (a - c) + (b - d)i
(3 + i) - (1 - 2i) = (3 - 1) + (1 - (-2))i
= 2 + 3i
Difference of Complex Numbers

6. Product of Complex Numbers

7. If z=a +bi is a complex number, then its conjugate,
denoted by

8. Theorem
The product of a complex number and its conjugate is a nonnegative real
number. Thus if z=a +bi, then

9. Theorem

11. If N is a positive real number, we define the principal square root of -N
as

12. In the complex number system, the solution of the quadratic equation
where a, b, and c are real numbers and
are given by the formula

13. Solve:

14. Discriminant of a Quadratic EquationDiscriminant of a Quadratic Equation
is called a discriminant
>0, there are 2 unequal real solutions.
=0, there is a repeated real solution.
<0, there are two complex solutions. The solutions are
conjugates of each other.

15. We can add, subtract, multiply or divide complex numbers. After
performing these operations if we’ve simplified everything correctly we
should always again get a complex number (although the real or
imaginary parts may be zero). Below is an example of each to refresh
your memory.
(3 – 2i) + (5 – 4i)ADDING
Combine real parts and
combine imaginary parts= 8 – 6i
(3 – 2i) - (5 – 4i)SUBTRACTING
= -2 +2i
Be sure to distribute the
negative through before
combining real parts and
imaginary parts3 – 2i - 5 + 4i
(3 – 2i) (5 – 4i)MULTIPLYING
FOIL and then combine like
terms. Remember i 2
= -1
= 15 – 12i – 10i+8i2
=15 – 22i +8(-1) = 7 – 22i
Notice when I’m done
simplifying that I only have two
terms, a real term and an
imaginary one. If I have more
than that, I need to simplify
more.

16. DIVIDING
i
i
45
23
−
−
Recall that to divide complex numbers, you multiply
the top and bottom of the fraction by the conjugate of
the bottom.
i
i
45
45
+
+
⋅
This means the same
complex number, but
with opposite sign on
the imaginary term
FOIL
2
2
16202025
8101215
iii
iii
−−+
−−+
=
12
−=i
( )
( )116202025
18101215
−−−+
−−−+
=
ii
ii
Combine like terms
41
223 i+
=
We’ll put the 41 under
each term so we can
see the real part and
the imaginary part
i
41
2
41
23
+=

17. Let’s solve a couple of equations that have complex
solutions to refresh our memories of how it works.
0252
=+x
-25 -25
252
−=x ±
ix 25±=
01362
=+− xx
a
acbb
x
2
42
−±−
=
Square root and
don’t forget the ±
The negative
under the square
root becomes i
Use the
quadratic
formula
( ) ( ) ( )( )
( )12
131466
2
−−±−−
=x
2
52366 −±
=
2
166 −±
=
2
166 i±
=
2
46 i±
= i23±=
i5±=

18. Powers of i
12
−=i
ii =
iiiii −=−== )(123
( )( ) 111224
=−−== iii
( ) iiiii === 145
( ) 111246
−=−== iii
( ) iiiii −=−== 1347
( ) 111448
=== iii
We could continue but notice
that they repeat every group
of 4.
For every i 4
it will = 1
To simplify higher powers
of i then, we'll group all the
i 4ths
and see what is left.
( ) ( ) iiiii ===
88433
1
4 will go into 33 8 times with 1 left.
( ) ( ) iiiii −=== 320320483
1
4 will go into 83 20 times with 3 left.

19. a
acbb
xcbxax
2
4
0
2
2 −±−
==++
If we have a quadratic equation and are considering solutions
from the complex number system, using the quadratic formula,
one of three things can happen.
3. The "stuff" under the square root can be negative and we'd get
two complex solutions that are conjugates of each other.
The "stuff" under the square root is called the discriminant.
This "discriminates" or tells us what type of solutions we'll have.
1. The "stuff" under the square root can be positive and we'd get
two unequal real solutions 04if 2
>− acb
2. The "stuff" under the square root can be zero and we'd get one
solution (called a repeated or double root because it would factor
into two equal factors, each giving us the same solution).04if 2
=− acb
04if 2
<− acb
The Discriminant acb 42
−=∆

20. Solving
Equations

21. A quadratic equation is an equation equivalent to one of the form
Where a, b, and c are real numbers and a ≠ 0
02
=++ cbxax
To solve a quadratic equation we get it in the form above and see if it will
factor.
652
−= xx Get form above by subtracting 5x and
adding 6 to both sides to get 0 on right side.
-5x + 6 -5x + 6
0652
=+− xx Factor.
( )( ) 023 =−− xx Use the Null Factor law and set each
factor = 0 and solve.
02or03 =−=− xx 3=x 2=x
So if we have an equation in x and the highest power is 2, it is
quadratic.

22. In this form we could have the case where b = 0.
02
=++ cbxax
Remember standard form for a quadratic equation is:
02
=+ cax002
=++ cxax
When this is the case, we get the x2
alone and then square root both sides.
062 2
=−x Get x2
alone by adding 6 to both sides and
then dividing both sides by 2
+ 6 + 6
62 2
=x
2 2
32
=x
Now take the square root of both
sides remembering that you must
consider both the positive and
negative root.
±
3±=x
Let's
check: ( ) 0632
2
=− ( ) 0632
2
=−−
066 =− 066 =−
Now take the square root of both
sides remembering that you must
consider both the positive and
negative root.

23. 02
=++ cbxax
What if in standard form, c = 0?
002
=++ bxax
We could factor by pulling an x
out of each term.
032 2
=− xx Factor out the common x
( ) 032 =−xx Use the Null Factor law and set each
factor = 0 and solve.
032or0 =−= xx
2
3
or0 == xx If you put either of these values in for
x in the original equation you can see
it makes a true statement.

24. 02
=++ cbxax
What are we going to do if we have non-zero values for a, b and c but
can't factor the left hand side?
0362
=++ xx
This will not factor so we will complete
the square and apply the square root
method.
First get the constant term on the other
side by subtracting 3 from both sides.362
−=+ xx
___3___62
+−=++ xx
We are now going to add a number to the left side so it will
factor into a perfect square. This means that it will factor into
two identical factors. If we add a number to one side of the
equation, we need to add it to the other to keep the equation
Let's add 9. Right now we'll see that it works and then we'll look at
how to find it.
9 9 6962
=++ xx

25. 6962
=++ xx Now factor the left hand
side.
( )( ) 633 =++ xx
two identical
factors
( ) 63
2
=+xThis can be written as:
Now we'll get rid of the square by
square rooting both sides.
( ) 63
2
=+x
Remember you need both the
positive and negative root!±
63 ±=+x Subtract 3 from both sides to get x
alone.
63 ±−=x
These are the answers in exact form.
We can put them in a calculator to get
two approximate answers.
55.063 −≈+−=x 45.563 −≈−−=x

26. Okay---so this works to solve the equation but how did we know to add 9
to both sides?
___3___62
+−=++ xx 9 9
( )( ) 633 =++ xx We wanted the left hand side to factor
into two identical factors.
When you FOIL, the outer terms and
the inner terms need to be identical
and need to add up to 6x.
+3 x
+3x
6 x
The last term in the original trinomial will then be the middle term's
coefficient divided by 2 and squared since last term times last term will be (3)
(3) or 32
.
So to complete the square, the number to add to both sides is…
the middle term's coefficient divided by 2 and
squared

27. Let's solve another one by completing the square.
02162 2
=+− xx To complete the square we want the
coefficient of the x2
term to be 1.
Divide everything by 20182
=+− xx
2 2 2 2
Since it doesn't factor get the constant on
the other side ready to complete the
square.
___1___82
+−=+− xx
So what do we add to both sides?
16=
16 16
Factor the left hand side( )( ) ( ) 15444
2
=−=−− xxx
Square root both sides (remember
±)
( ) 154
2
±=−x
154 ±=−x 154 ±=xAdd 4 to both sides to
get x alone
2
2
8





 −
the middle term's coefficient divided by 2 and squared

28. By completing the square on a general quadratic equation in
standard form we come up with what is called the quadratic
formula. (Remember the song!! )
a
acbb
x
2
42
−±−
=
This formula can be used to solve any quadratic equation whether it factors
or not. If it factors, it is generally easier to factor---but this formula would give
you the solutions as well.
We solved this by completing the square
but let's solve it using the quadratic
formula
a
acbb
x
2
42
−±−
=
1
(1
)
(1)
6 6
(3)
2
12366 −±−
=
Don't make a mistake with order of
operations! Let's do the power and the
02
=++ cbxax
0362
=++ xx

29. 2
12366 −±−
=x
2
246 ±−
=
626424 =×=
2
626 ±−
=
( )
2
632 ±−
=
There's a 2 in common in
the terms of the
numerator
63±−= These are the solutions we got
when we completed the square on
this problem.
NOTE: When using this formula if you've simplified under the radical and end
up with a negative, there are no real solutions.
(There are complex (imaginary) solutions, but that will be dealt with in year 12
Calculus).

30. SUMMARY OF SOLVING QUADRATIC EQUATIONS
Get the equation in standard form: 02
=++ cbxax
If there is no middle term (b = 0) then get the x2
alone and square root both
sides (if you get a negative under the square root there are no real
solutions).
If there is no constant term (c = 0) then factor out the common x and use the
null factor law to solve (set each factor = 0).
If a, b and c are non-zero, see if you can factor and use the null factor law to
solve.
If it doesn't factor or is hard to factor, use the quadratic formula to solve (if
you get a negative under the square root there are no real solutions).

31. a
acbb
xcbxax
2
4
0
2
2 −±−
==++
If we have a quadratic equation and are considering solutions from the real
number system, using the quadratic formula, one of three things can happen.
3. The "stuff" under the square root can be negative and we'd get no real
solutions.
The "stuff" under the square root is called the discriminant.
This "discriminates" or tells us what type of solutions we'll have.
1. The "stuff" under the square root can be positive and we'd get two
unequal real solutions
04if 2
>− acb
2. The "stuff" under the square root can be zero and we'd get one solution
(called a repeated or double root because it would factor into two equal
factors, each giving us the same solution).
04if 2
=− acb
04if 2
<− acb
The Discriminant acb 42
−=∆

32. Acknowledgement
I wish to thank Shawna Haider from Salt Lake Community College,
Utah USA for her hard work in creating this PowerPoint.
www.slcc.edu
Shawna has kindly given permission for this resource to be
downloaded from www.mathxtc.com and for it to be modified to suit
the Western Australian Mathematics Curriculum.
Stephen Corcoran
Head of Mathematics
St Stephen’s School – Carramar
www.ststephens.wa.edu.au

33. THANKS FORTHANKS FOR
WATCHING!!!WATCHING!!!