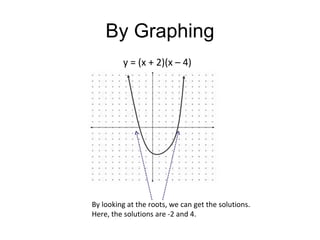
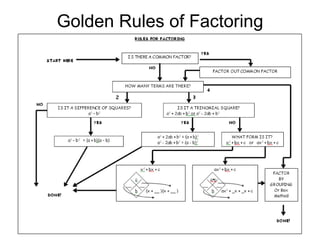
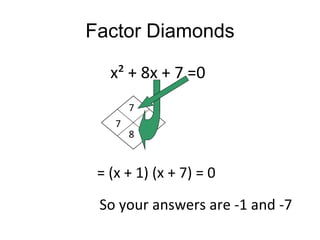
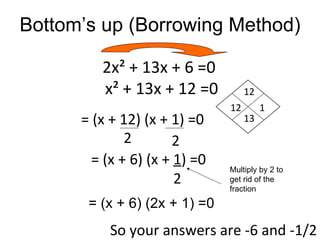
1) There are several methods for solving quadratic equations, including factoring, graphing, using the quadratic formula, and completing the square. 2) Factoring involves expressing the quadratic expression as a product of two linear factors. Methods for factoring include finding the greatest common factor, using factor diamonds, grouping, and the borrowing method. 3) The document provides examples of solving quadratics using various factoring techniques and practicing additional problems.

1. Factoring Quadratic
Expressions

2. WAYS TO SOLVE A QUADRATIC
EQUATION ax² + bx + c = 0
• There are many ways to solve a quadratic.
• The main ones are:
– Graphing
– Factoring
– Bottom’s Up
– Grouping
– Quadratic formula
– Completing the square

3. By Graphing
y = (x + 2)(x – 4)
By looking at the roots, we can get the solutions.
Here, the solutions are -2 and 4.

4. Golden Rules of Factoring

5. Example: Factor out the greatest
common factor
• 4x2 + 20x -12

6. Practice: Factor each expression
a) 9x2 + 3x – 18 Solutions:
a.) 3(3x2 + x – 6)
b) 7p2 + 21
b) 7(p2 + 3)
c) 4w2 + 2w
c) 2w(2w + 1)

7. Factor Diamonds
x² + 8x + 7 =0
7
7 1
8
= (x + 1) (x + 7) = 0
So your answers are -1 and -7

8. Practice: Solve by a factor diamond
• X2 + 15x + 36
(x+3)(x+12)

9. Bottom’s up (Borrowing Method)
2x² + 13x + 6 =0
x² + 13x + 12 =0 12
12 1
= (x + 12) (x + 1) =0 13
2 2
= (x + 6) (x + 1) =0 Multiply by 2 to
2 get rid of the
fraction
= (x + 6) (2x + 1) =0
So your answers are -6 and -1/2

10. Practice: Solve using
Bottom’s Up/Barrowing Method
• 2x2 – 19x + 24
(x-8)(2x-3)

11. Factor by Grouping
2x² – 7x – 15 =0
-30 2x² – 10x + 3x – 15 =0
-10 3
-7 Note: you are
on the right
2x(x – 5) + 3(x – 5) =0 track because
you have (x-5)
in both
(2x + 3)(x – 5)=0 parenthesis
So your answers are -3/2 and 5

12. Practice: Factor by Grouping
3x2 + 7x - 20
(x+4)(3x-5)

13. SHORTCUTS
• a2 + 2ab + b2 (a+b)2
Example: 25x2 + 90x + 81 (5x + 9)2
• a2 - 2ab + b2 (a - b)2
Example: 9x2 – 42x + 49 (3x – 7)2
• a2 - b2 (a+b)(a - b)
Example: x2 – 64 (x + 8)(x – 8)

14. Practice Problems: Solve using any
method
Solutions:
• 3x2 – 16x – 12
a)(x-6)(3x+2)
• 4x2 + 5x – 6
• 4x2 – 49 c) (x+2)(4x-3)
• 2x2 + 11X + 12 d)(2x+7)(2x-7)
e)(x+4)(2x+3)