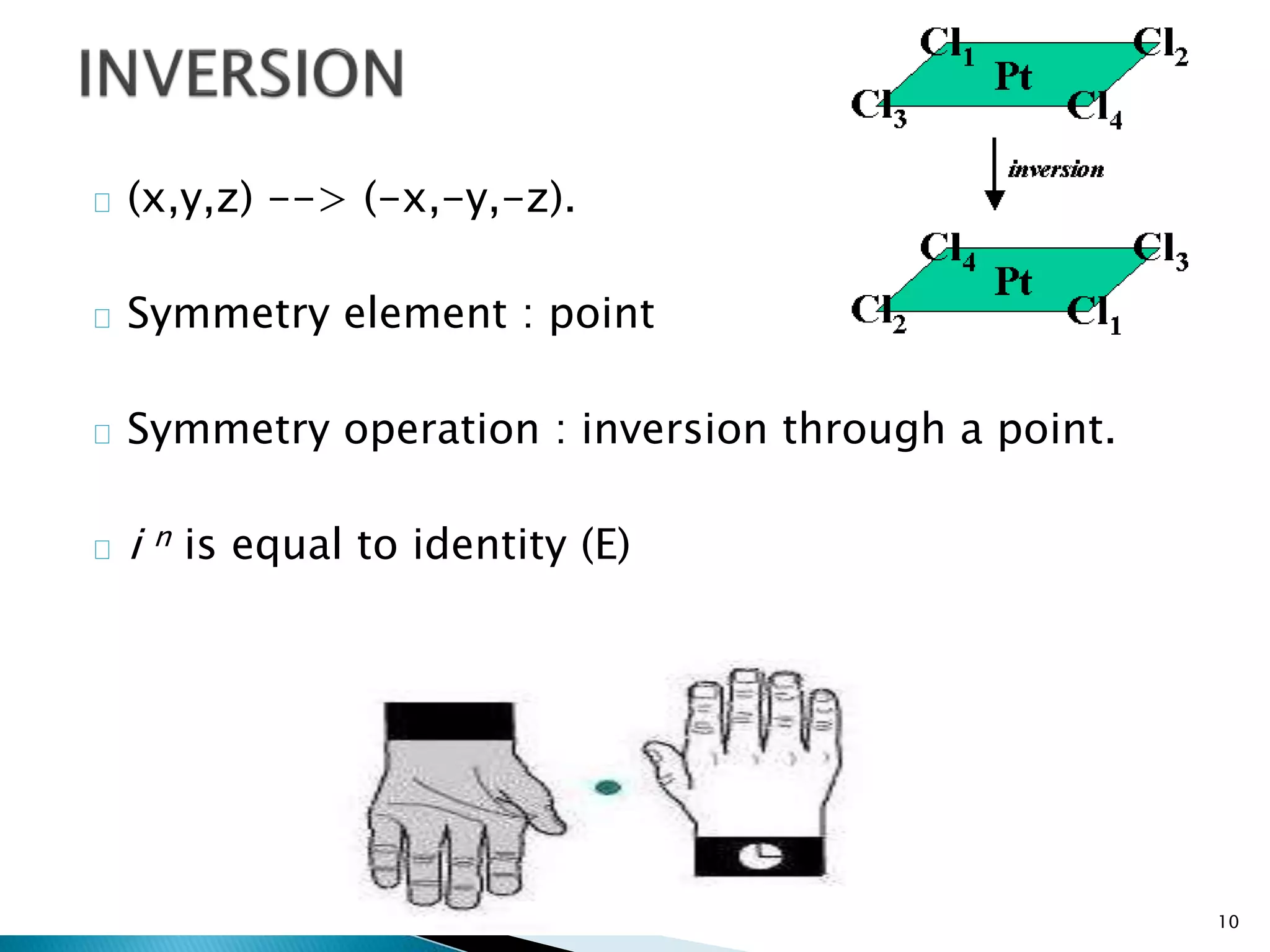
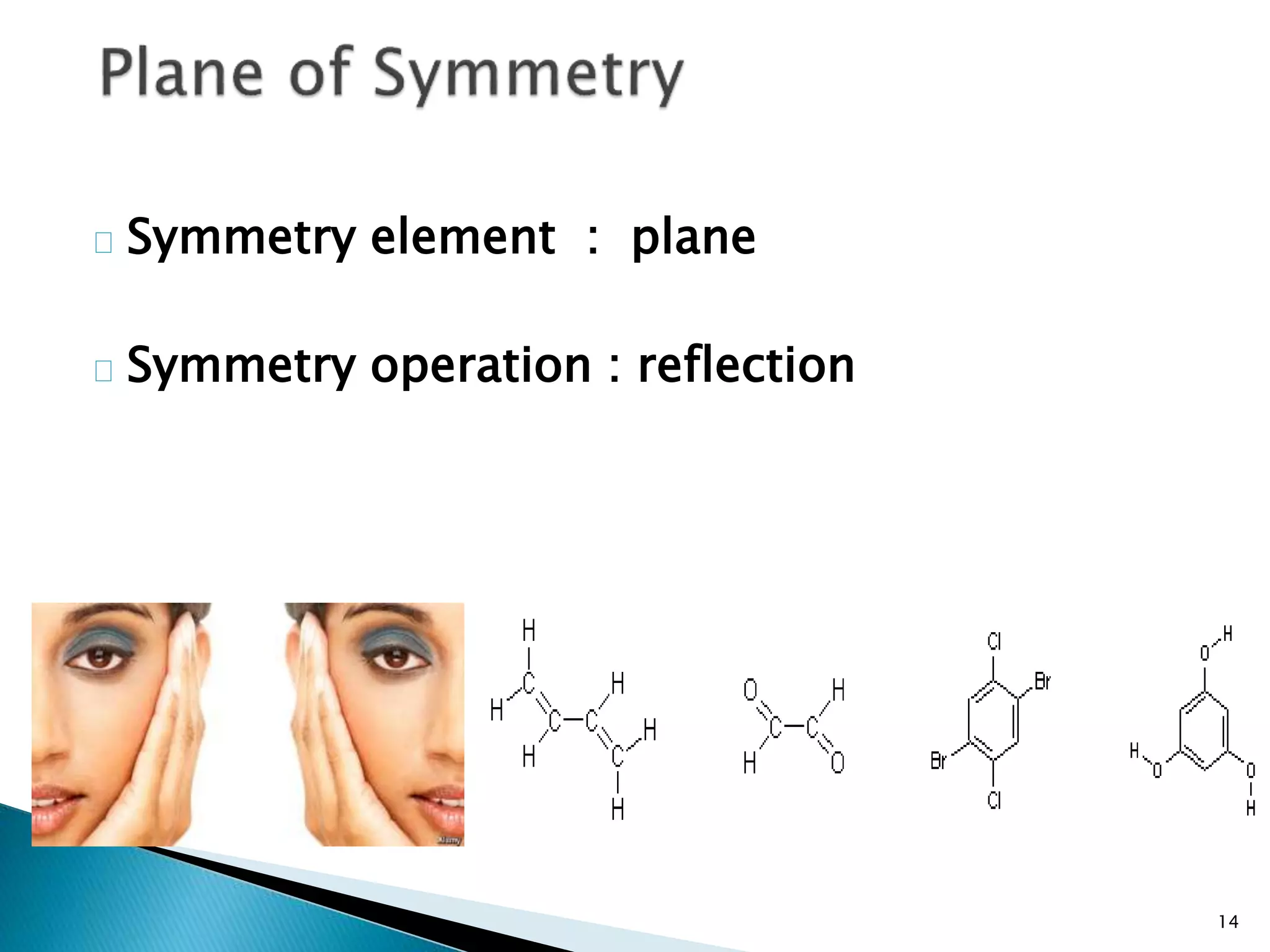
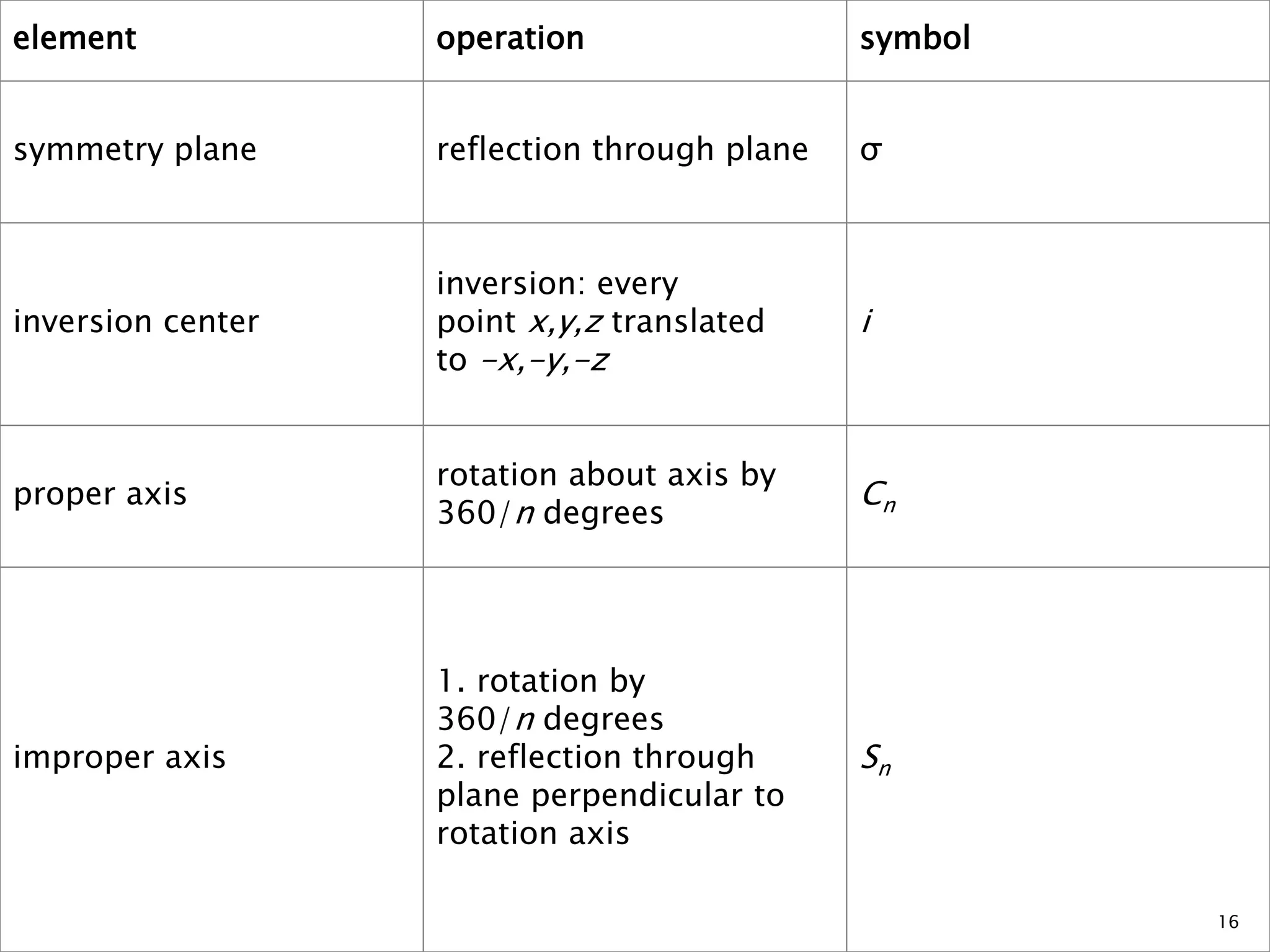
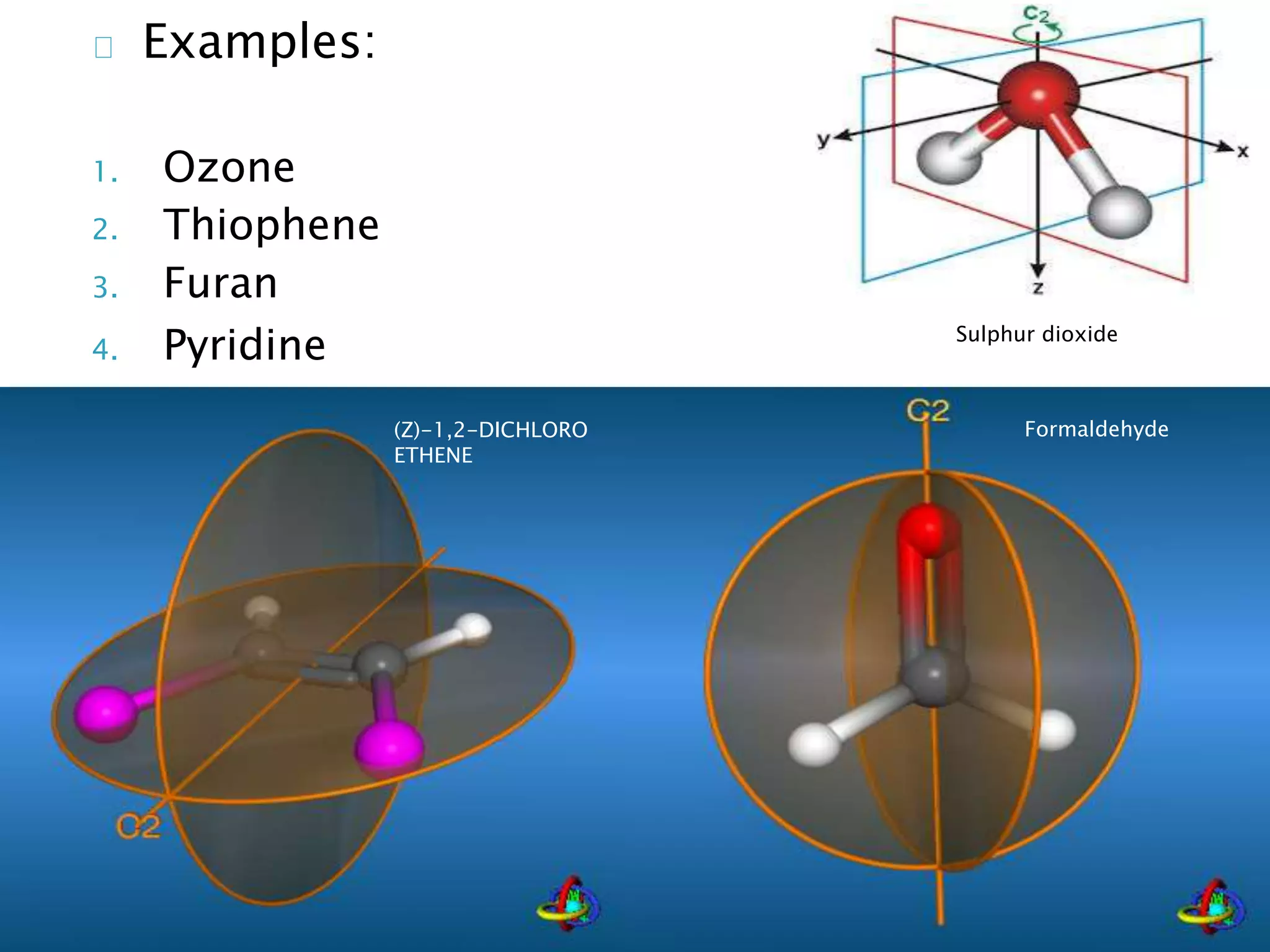
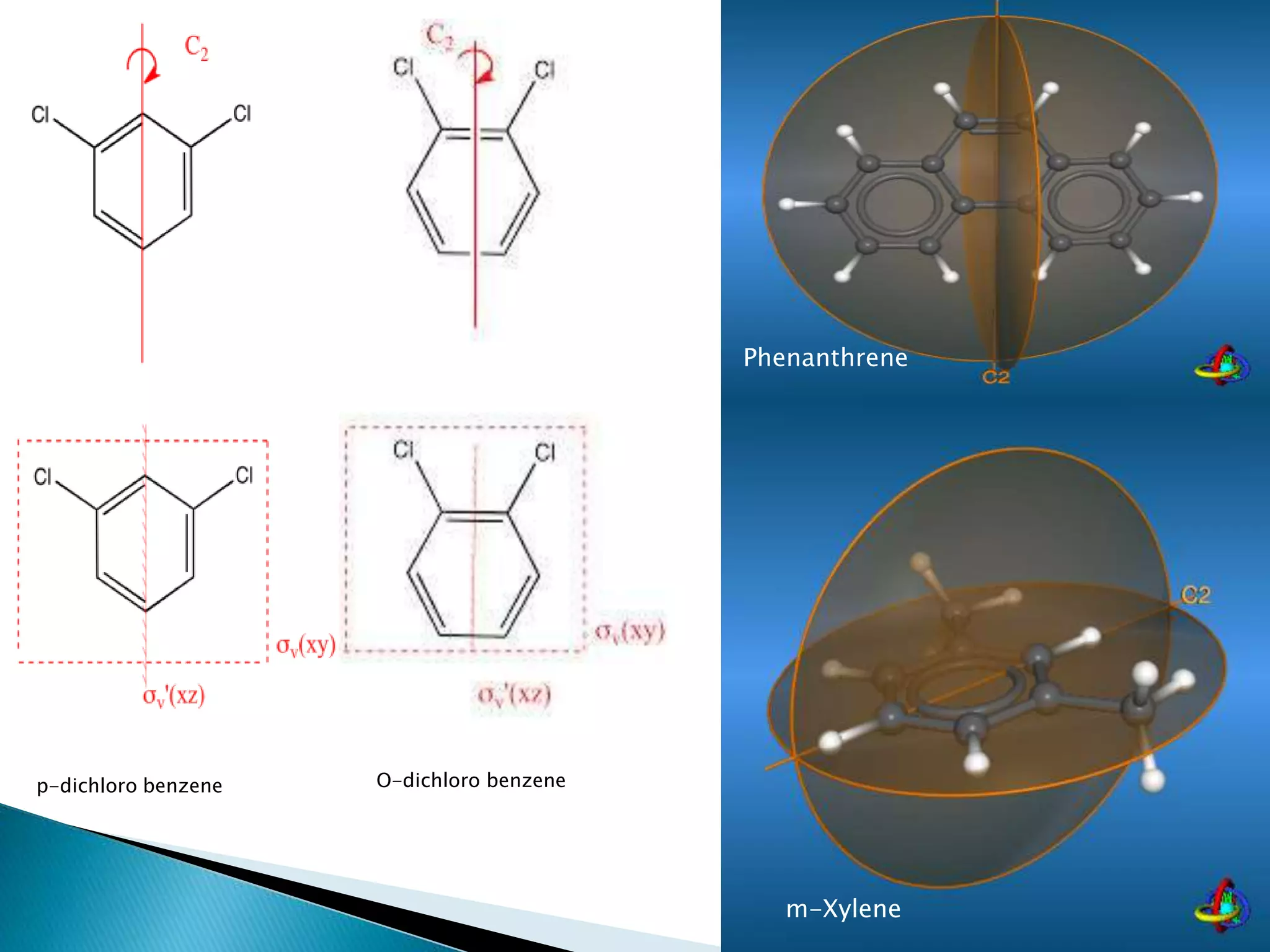
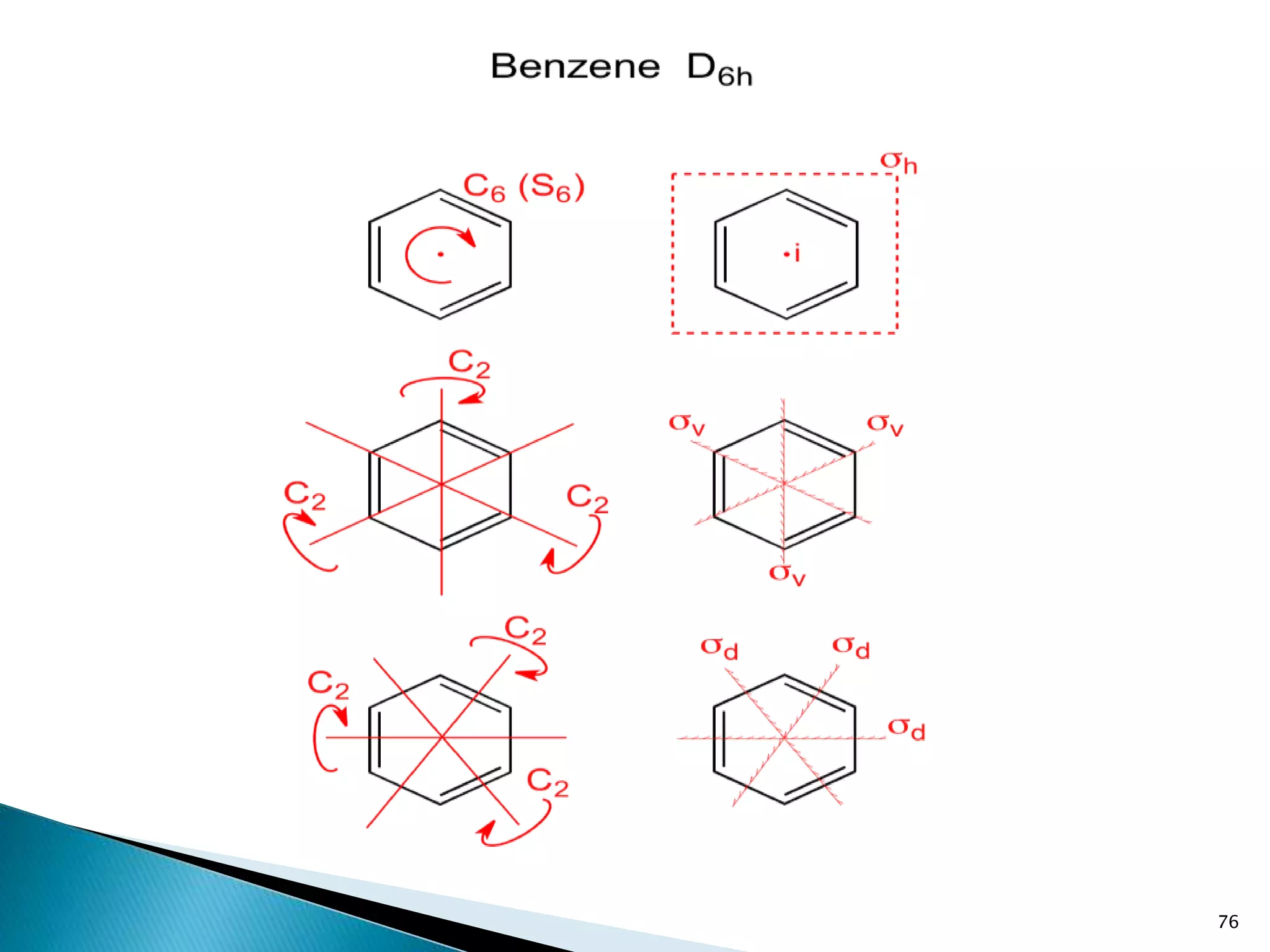
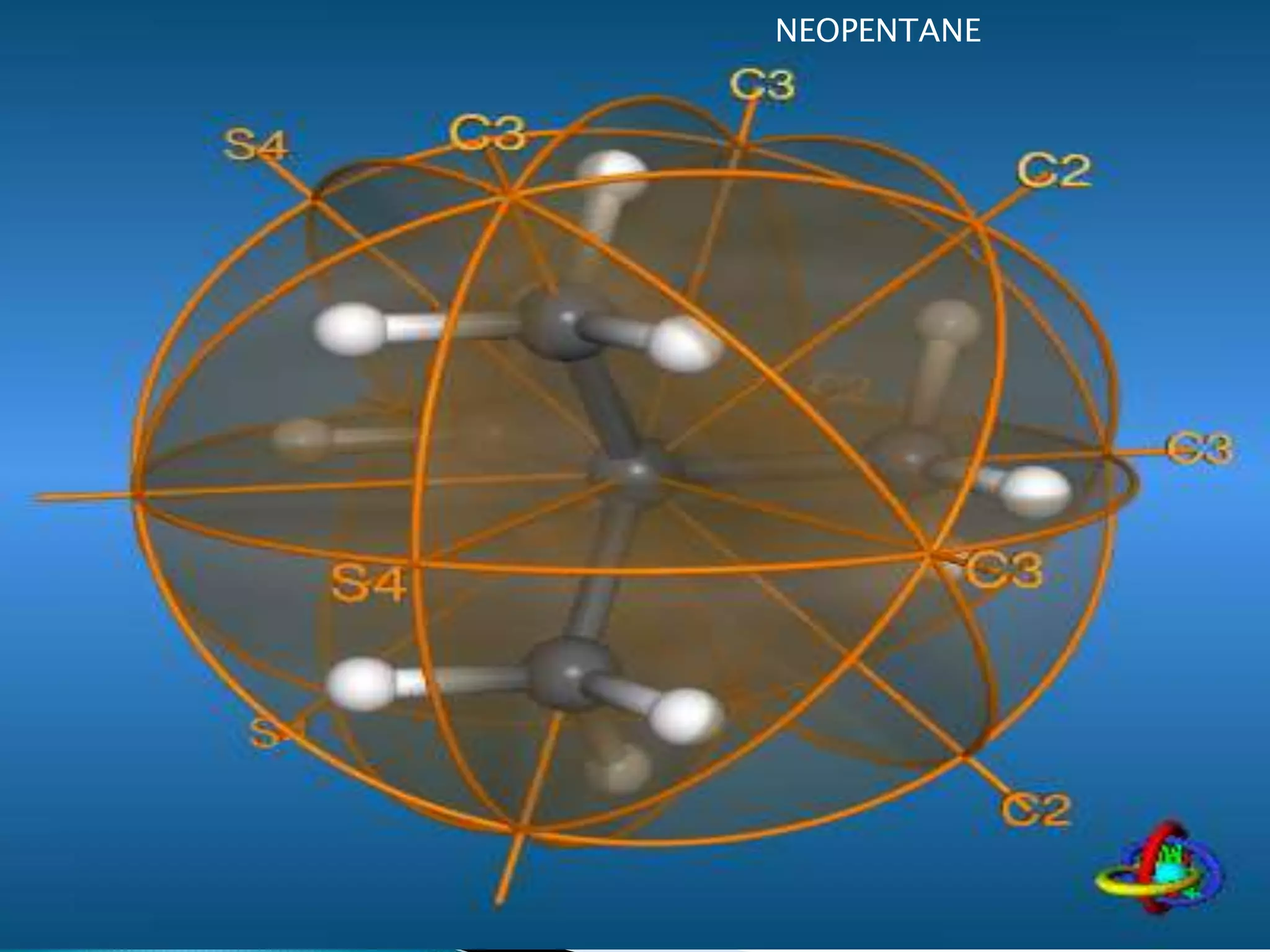
The document discusses symmetry operations and point groups in molecules. It defines five basic symmetry operations: identity, n-fold rotation, reflection, inversion, and improper n-fold rotation. Point groups describe the symmetry elements and operations in a molecule. There are 32 possible point groups that molecules can belong to depending on their specific symmetry properties. The document provides examples of molecules and their corresponding point groups.

1. Done by
Shobana.N.S
1
BY
SHOBANA.N.S
QUEEN MARY’S COLLEGE

2. 2

3. Symmetry is present in nature and in human
culture
3

4. Understand what orbitals are used
in bonding.
Predict optical activity of a
molecule.
Predict IR and Raman spectral
activity
4

5. A molecule or object is said to possess a
particular operation if that operation when
applied leaves the molecule unchanged.
5

6. There are 5 kinds of
operations
1. Identity
2. n-Fold Rotations
3. Reflection
4. Inversion
5. Improper n-Fold Rotation
6

7. IDENTITY
 E (Identity Operation) = no change in the
object.
 Needed for mathematical completeness.
 Every molecule has at least this symmetry
operation.
7

8. It is equal to rotation of the object 360/n
degree about an axis .
The symmetry element is line.
Principle axis = axis with the largest
possible n value.
n Is equal to identity (E)
Cn
8

9. Symmetry element is plane.
Linear object has infinite σ.
σv- plane including principle axis
σh- plane perpendicular to principle axis.
σd- plane bisecting the dihedral angle between two σv plane.
9

10. (x,y,z) --> (-x,-y,-z).
Symmetry element : point
Symmetry operation : inversion through a point.
i n is equal to identity (E)
10

11. It is also known as ROTATION-REFLECTION AXIS.
Rotation followed by reflection.
n = E ( n= even number)
Sn
2n = E ( n= odd number)
Sn
11

12. A symmetry element is a point of reference
about which symmetry operations can take
place
Symmetry elements can be
1. point
2. axis and
3. plane
12

13. Symmetry element : point
Symmetry operation : inversion
1,3-trans-disubstituted cyclobutane
13

14. Symmetry element : plane
Symmetry operation : reflection
14

15. Symmetry element : line
Symmetry operation : rotation
15

16. element operation symbol
symmetry plane reflection through plane σ
inversion center
inversion: every
point x,y,z translated
to -x,-y,-z
i
proper axis
rotation about axis by
360/n degrees
Cn
improper axis
1. rotation by
360/n degrees
2. reflection through
plane perpendicular to
rotation axis
Sn
16

17. 17

18. The collection of symmetry elements present
in a molecule forms a ‘group’, typically called
a POINT GROUP.
The symmetry elements can combine only in a
limited number of ways and these
combinations are called the POINT GROUP.
WHY IS IT CALLED A “POINT GROUP”??
 Because all the symmetry elements (points,
lines, and planes) will intersect at a single
point.
18

19. 19

20. Ci has 2 symmetry operations :
E the identity operation
i point of inversion
20
C2H2F2Cl2

21. It has two symmetry operations
E – identity operation
σ – reflection
21
CH2BrCl
1- bromo, 2-chloro ethene

22. Only one symmetry operation (E)
Molecules in this group have no symmetry
This means no symmetrical operations
possible.
22
Bromochlorofluoromethane CHFBrCl

23. Rotation of the molecule to 180 degree.
This point group contains only two
symmetry operations:
E the identity operation
C2 a twofold symmetry axis
Examples : water, chlorine
trifluoride, hydrogen peroxide,
formaldehyde
23
hydrazine

24. 24
(2R,3R)-tartaric acid D-mannitol

25. Rotation of the molecule to 120 degree.
This point group contains only two symmetry operations:
E the identity operation
C3 a three fold symmetry axis
Examples: ammonia, boron trifluoride,
triphenyl phosphine
25

26. 26
9b H-Phenalene 3,7,11-trimethyl cyclo dodeca 1,5,9-triene
2,6,7-trimethyl-1-aza-bicyclo
[2.2.2]octane

27. This point group contains the following symmetry
operations
E the identity operation
Cn n-fold symmetry axis.
nσv n reflection operation
27

28. This point group contains the following
symmetry operations
E the identity operation
C2 2-fold symmetry axis.
2σv reflection operation
28

29. Examples:
1. Ozone
2. Thiophene
3. Furan
4. Pyridine
29
Sulphur dioxide
(Z)-1,2-DICHLORO Formaldehyde
ETHENE

30. 30
Phenanthrene
m-Xylene
p-dichloro benzene O-dichloro benzene

31. 31

32. 32
Cyclohexane (boat) Water

33. This point group contains the following
symmetry operations
E the identity operation
C3 3-fold symmetry axis.
3σv reflection operation
33

34. Examples:
34
Ammonia POCl3 Trichloro methane
Tert-butyl bromide

35. This point group contains the following
symmetry operations
E the identity operation
C4 n-fold symmetry axis.
4σv n reflection operation
35

36. 36
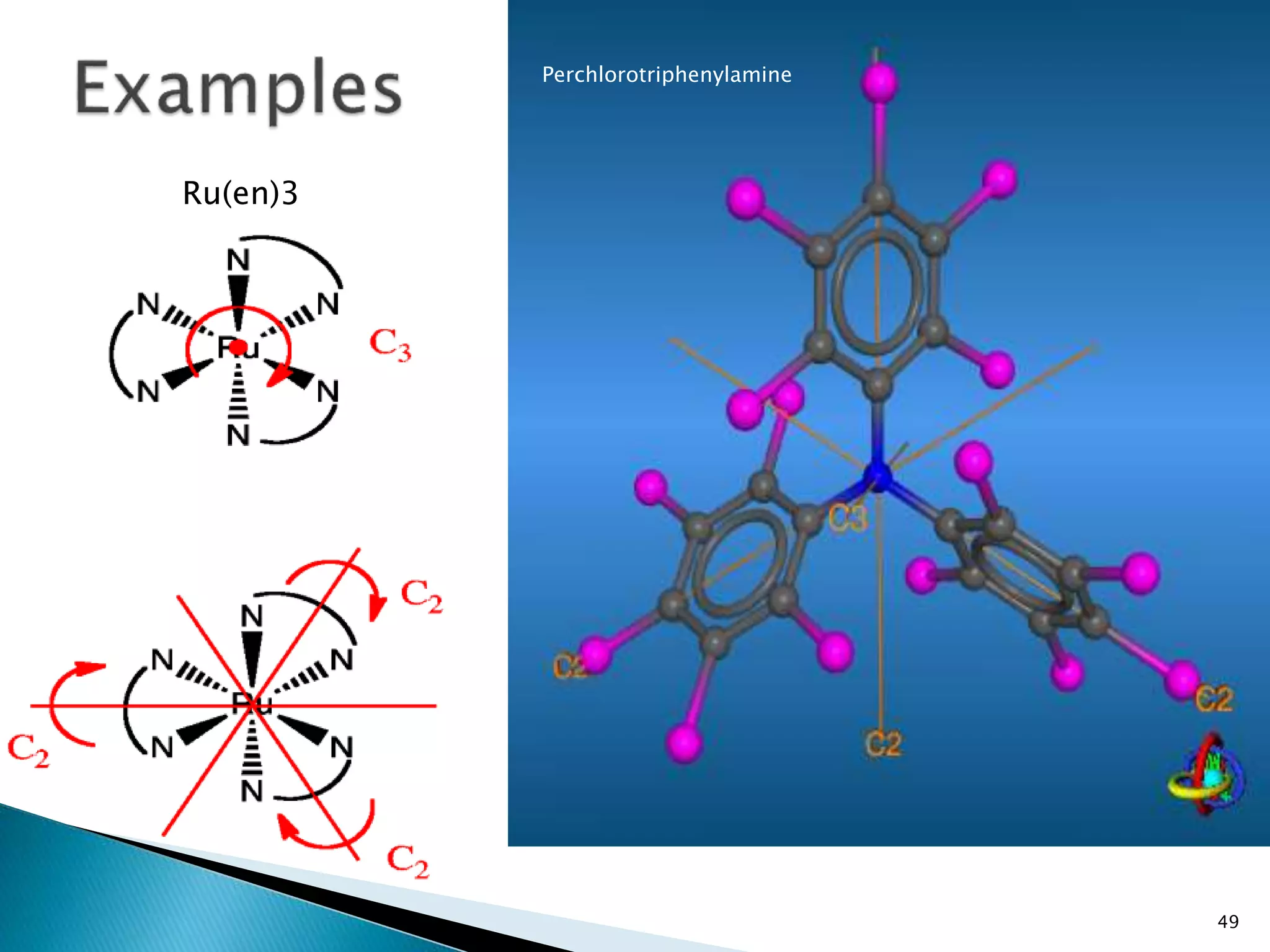
EXAMPLES
Xenon oxytetrafluoride
Sulfur chloride pentafluoride
Bromine pentafluoride
Fluorine pentafluoride
Calix[4]arene

37. This point group contains the following
symmetry operations
E the identity operation
C∞ ∞ -fold symmetry axis.
∞ σv n reflection operation
37

38. Linear Hetero nuclear Diatomic Molecule
belongs to this category
These molecules don’t have centre of
inversion.
38
Chloro ethyne

39. This point group contains the following
symmetry operations
E the identity operation
Cn n-fold symmetry axis.
σh n reflection operation
NOTE : If n is even ‘i’ is present.
39

40. This point group contains the following
symmetry operations
E the identity operation
C2 2-fold symmetry axis.
σh reflection operation
i inversion
40

41. 41
EXAMPLES
trans-1,2-dichloroethylene
Trans-1,3-butadiene
C2H2F2
N2F2

42. 42
1,4-dibromo-2,5-dichloro-benzene (E)-1,2-dichloro ethene

43. This point group contains the following
symmetry operations
E the identity operation
C3 3-fold symmetry axis.
σh reflection operation
S3 improper axis of symmetry
43

44. 44
Benzene-1,3,5-triol

45. 45

46. This point group contains the following
symmetry operations
E the identity operation
Cn n-fold symmetry axis.
nC2 2-fold symmetry axis.
(perpendicular to Cn)
46

47. This point group contains the following
symmetry operations
E the identity operation
C2 n-fold symmetry axis.
2C2 2-fold symmetry axis.
47
twistane

48. 48
This point group contains the following
symmetry operations
E the identity operation
C3 3-fold symmetry axis.
3C2 2-fold symmetry axis.

49. 49
Ru(en)3
Perchlorotriphenylamine

50. 50
Tris(oxalato)iron111
Molecular knot

51. This point group contains the following
symmetry operations
E the identity operation
Cn n-fold symmetry axis.
nC2 2-fold symmetry axis.
nσd dihedral plane
51
NOTE : ‘i’ is present when n is odd and S2n coincident to C2 axis

52. This point group contains the following
symmetry operations
E the identity operation
C2 n-fold symmetry axis.
2C2* 2-fold symmetry axis.
2σd dihedral plane
2S4 improper axis of symmetry
52

53. 53
allene (propa-1,2-diene) biphenyl

54. 54
1,3,5,7-COT

55. This point group contains the following
symmetry operations
E the identity operation
C3 n-fold symmetry axis.
2C2 2-fold symmetry axis.
3σd dihedral plane
2S6 improper axis of symmetry
55

56. 56
Cyclohexane chair form

57. 57
Ethane staggered form

58. This point group contains the following symmetry operations
E the identity operation
2C4 n-fold symmetry axis.
4C2* 2-fold symmetry axis.
4σd dihedral plane
S8 improper axis of symmetry
C2 2-fold symmetry axis.
58
Mn2(CO)10

59. This point group contains the following symmetry
operations
E the identity operation
4C5 n-fold symmetry axis.
5C2* 2-fold symmetry axis.
5σd dihedral plane
S10 improper axis of symmetry
i inversion
59

60. 60

61. This point group contains the following symmetry
operations
E the identity operation
Cn n-fold symmetry axis.
nC2 2-fold symmetry axis.
σh horizontal plane
nσv vertical plane
Sn improper axis of symmetry
61

62. 62
This point group contains the following symmetry
operations
E the identity operation
C2 n-fold symmetry axis.
2C2 2-fold symmetry axis.
σh horizontal plane
2σv vertical plane
S2 improper axis of symmetry

63. 63
M2F6
DIBORANE
ETHENE

64. 64

65. 65
1,4-DICHLOROBENZENE

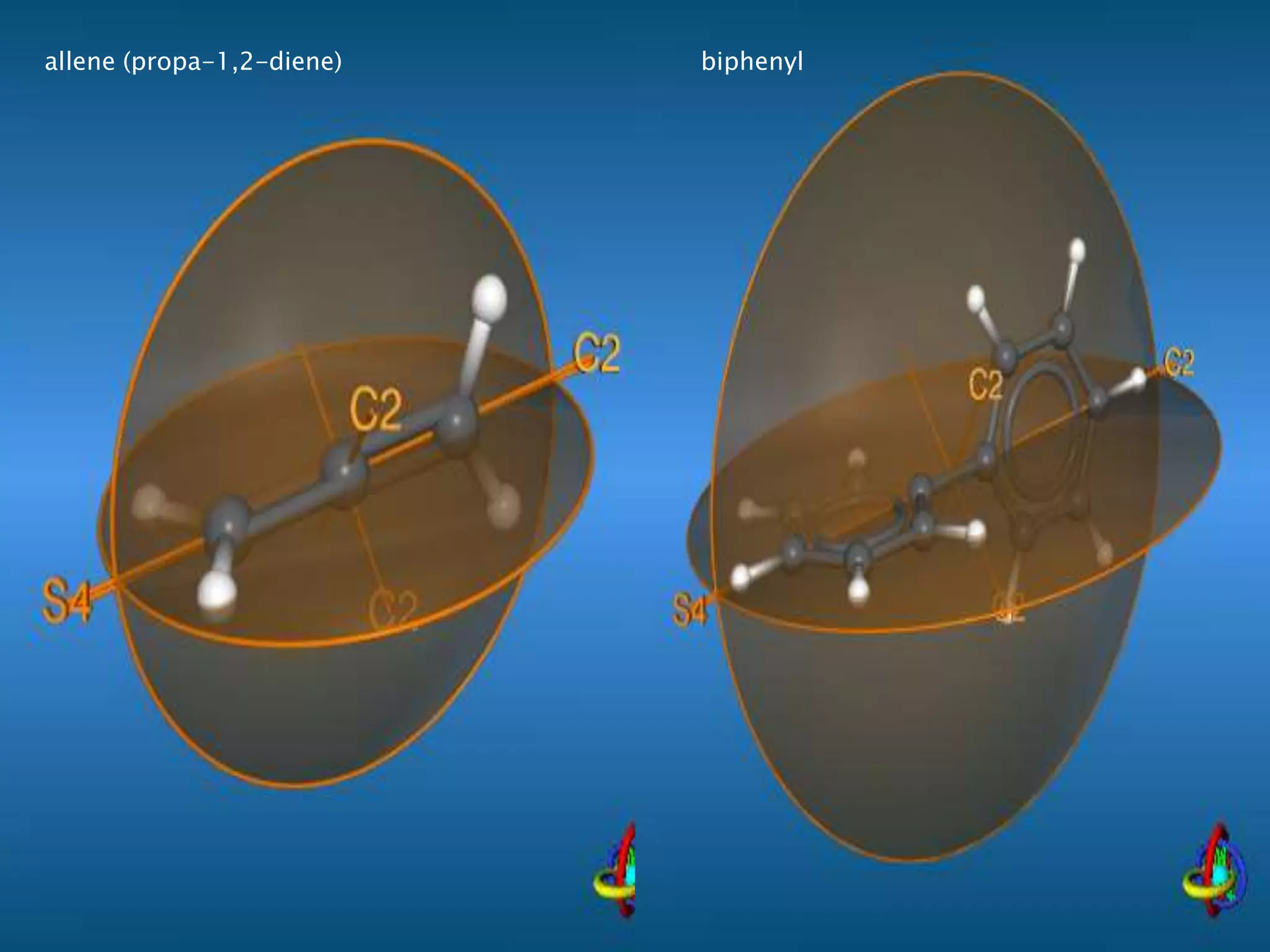
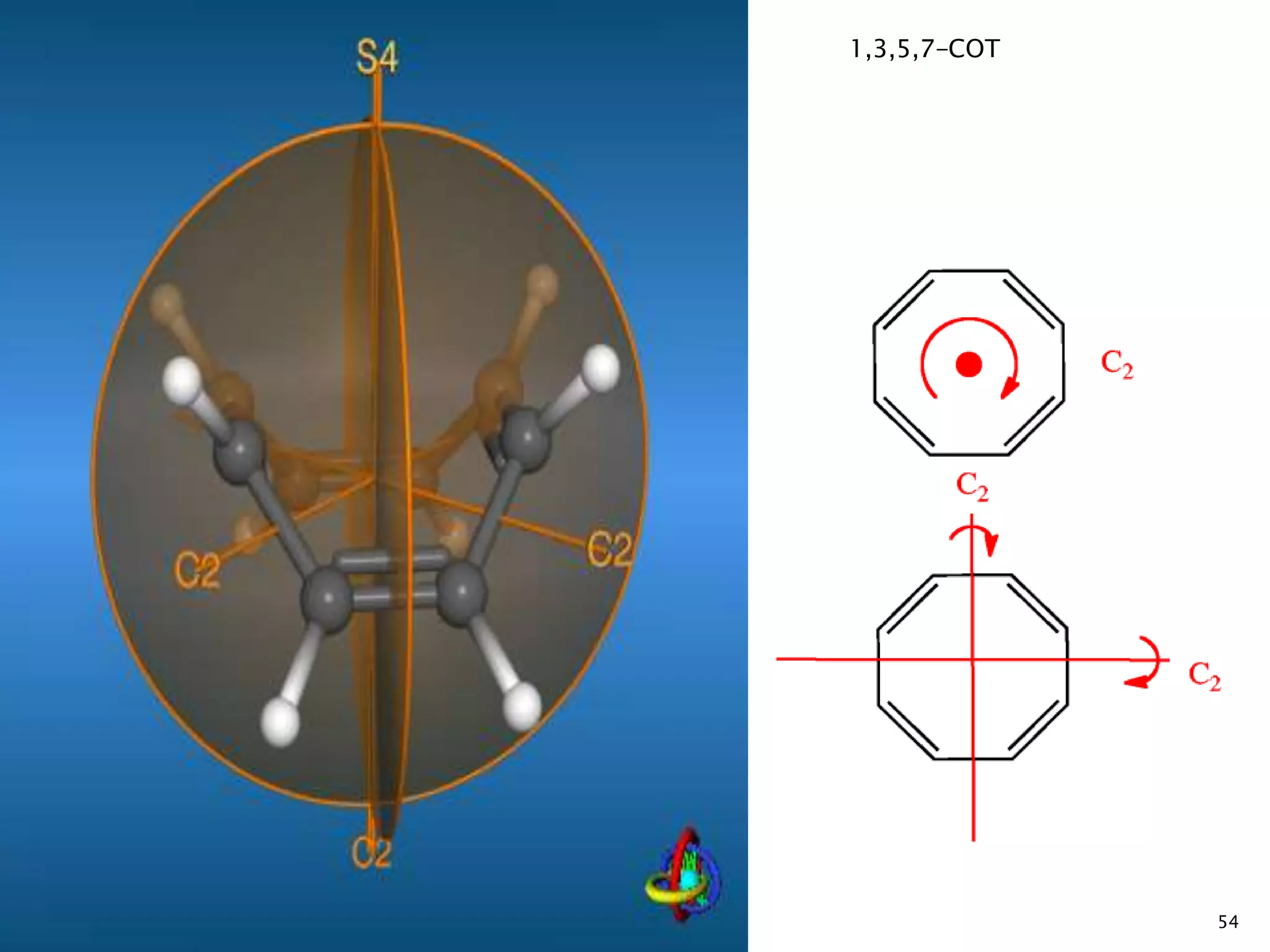
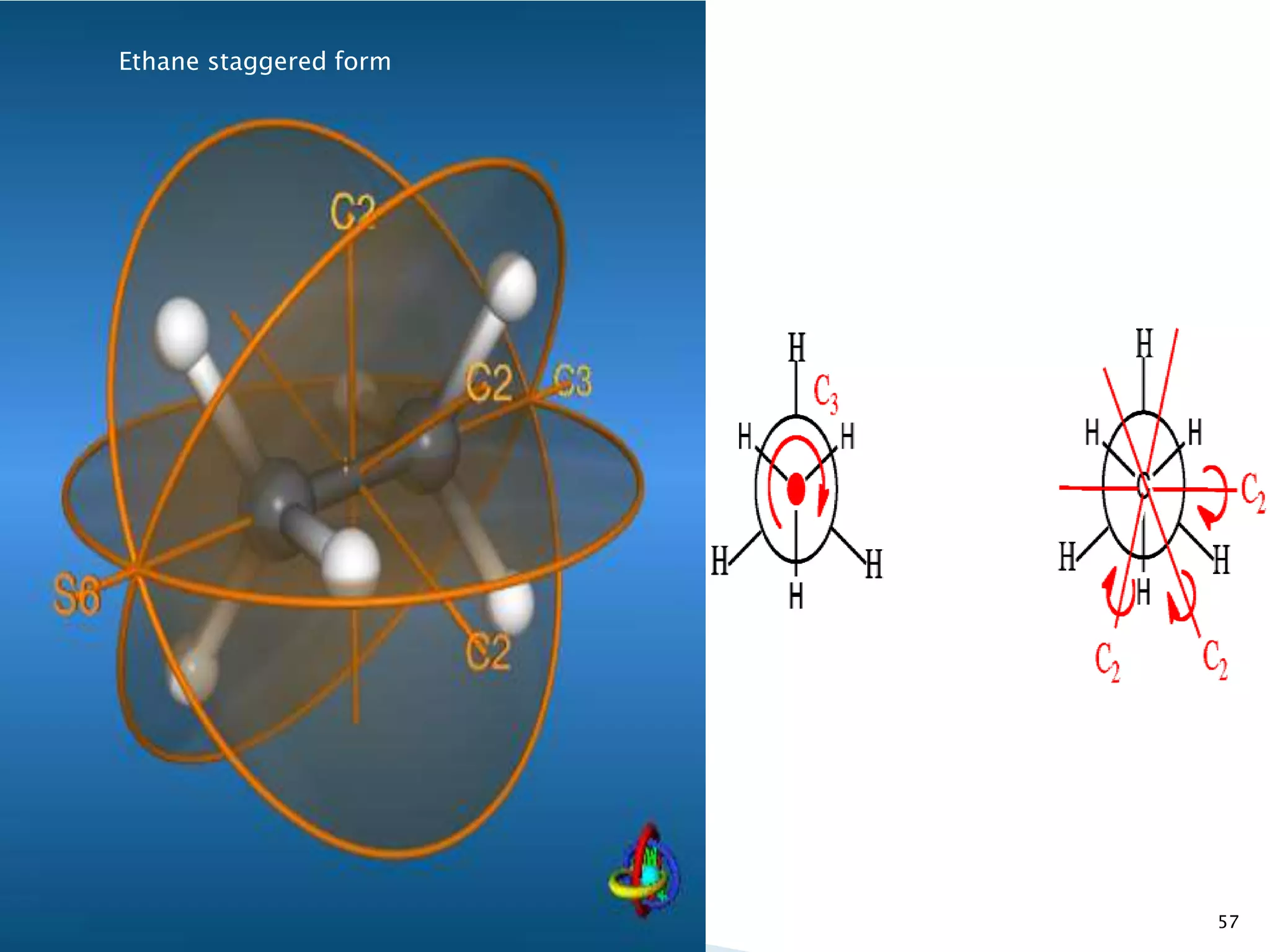
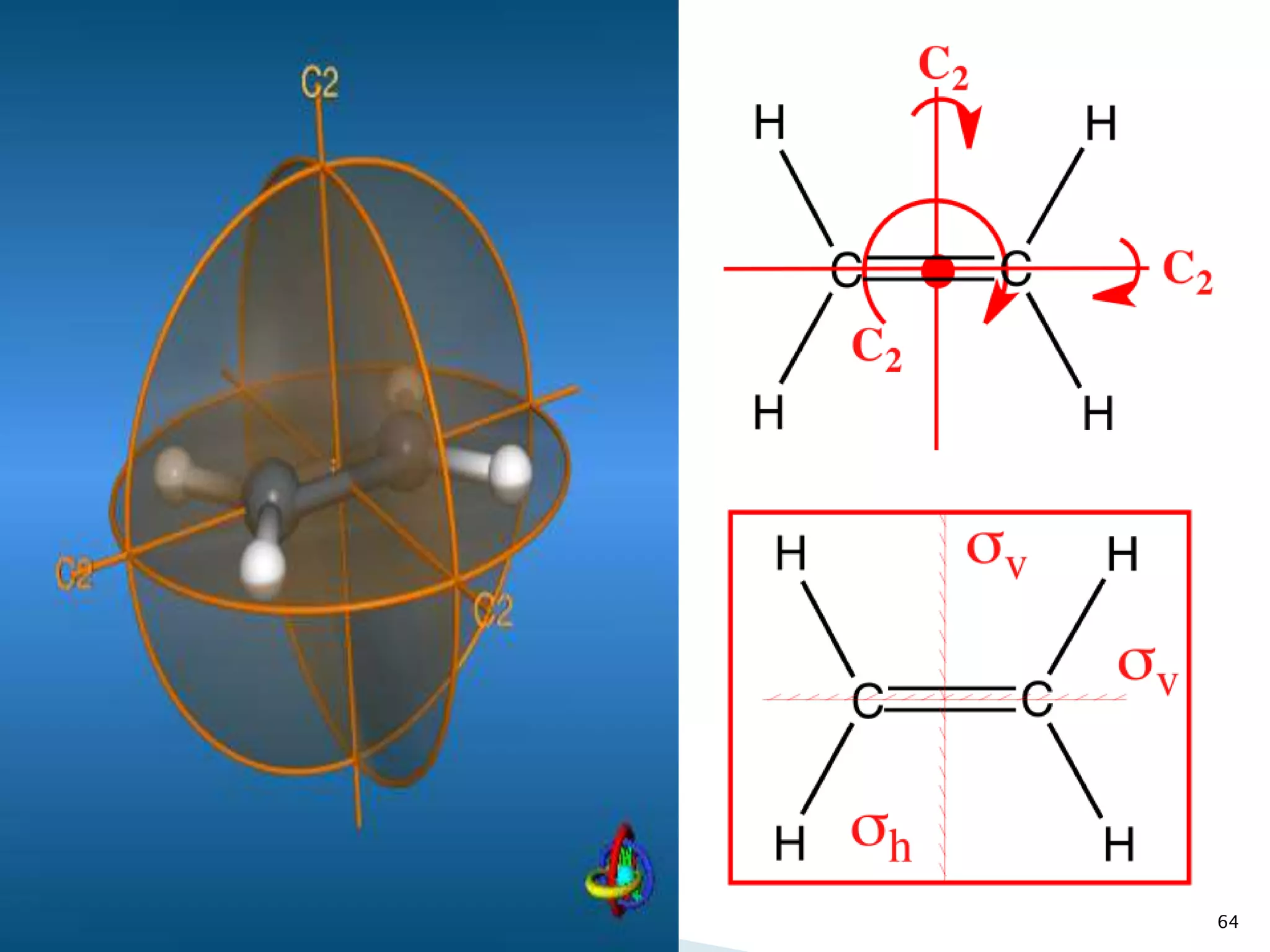
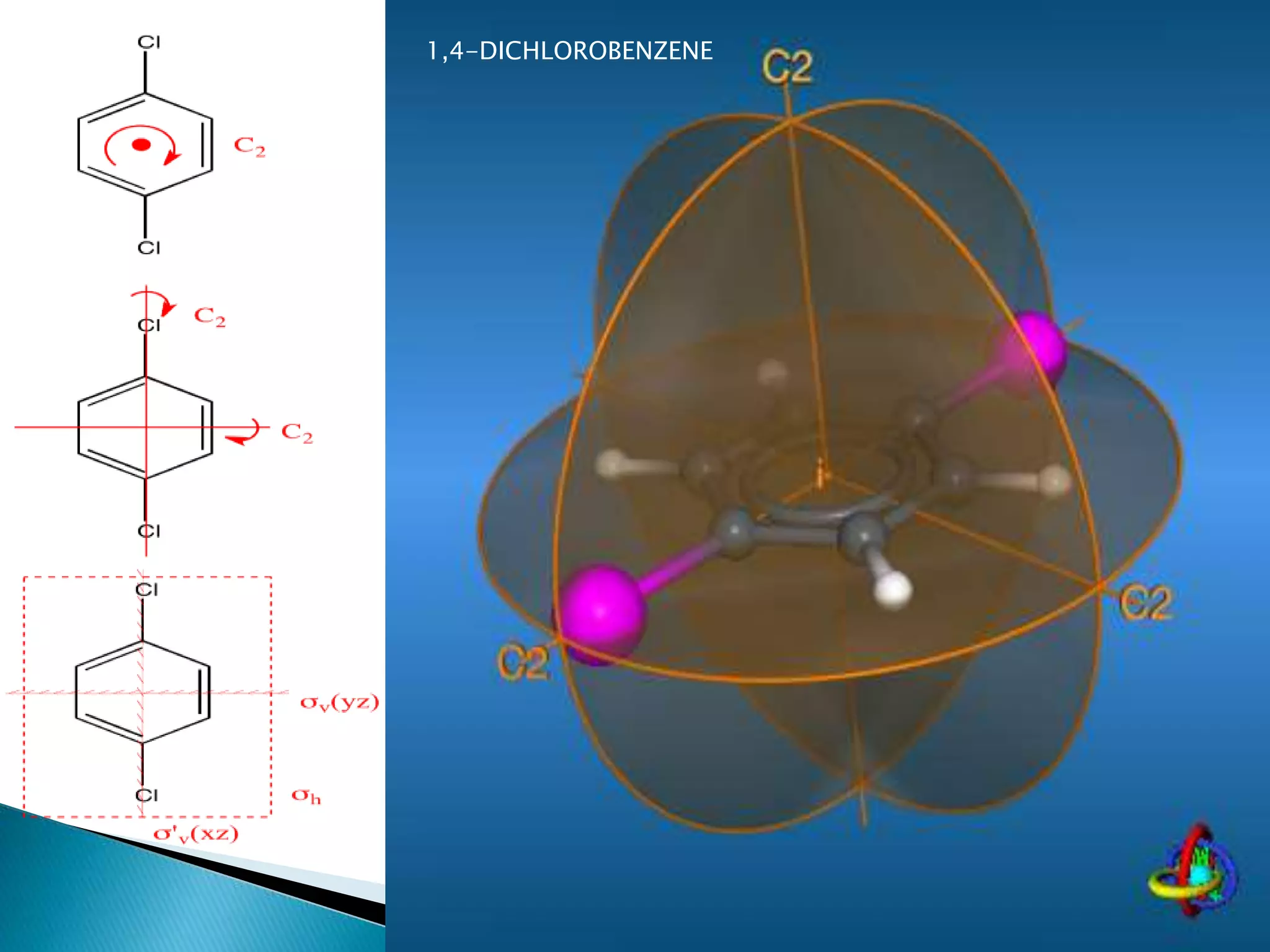
66. 66
[2,2] PARACYCLOPHANE

67. 67
This point group contains the following symmetry
operations
E the identity operation
C3 3-fold symmetry axis.
3C2 2-fold symmetry axis.
σh horizontal plane
2σv vertical plane
2S3 improper axis of symmetry

68. 68

69. 69
cyclopropane

70. 70
This point group contains the following symmetry
operations
E the identity operation
C4 4-fold symmetry axis.
4C2 2-fold symmetry axis.
σh horizontal plane
4σv vertical plane
S4 improper axis of symmetry

71. 71
Nickel tetracarbonyl

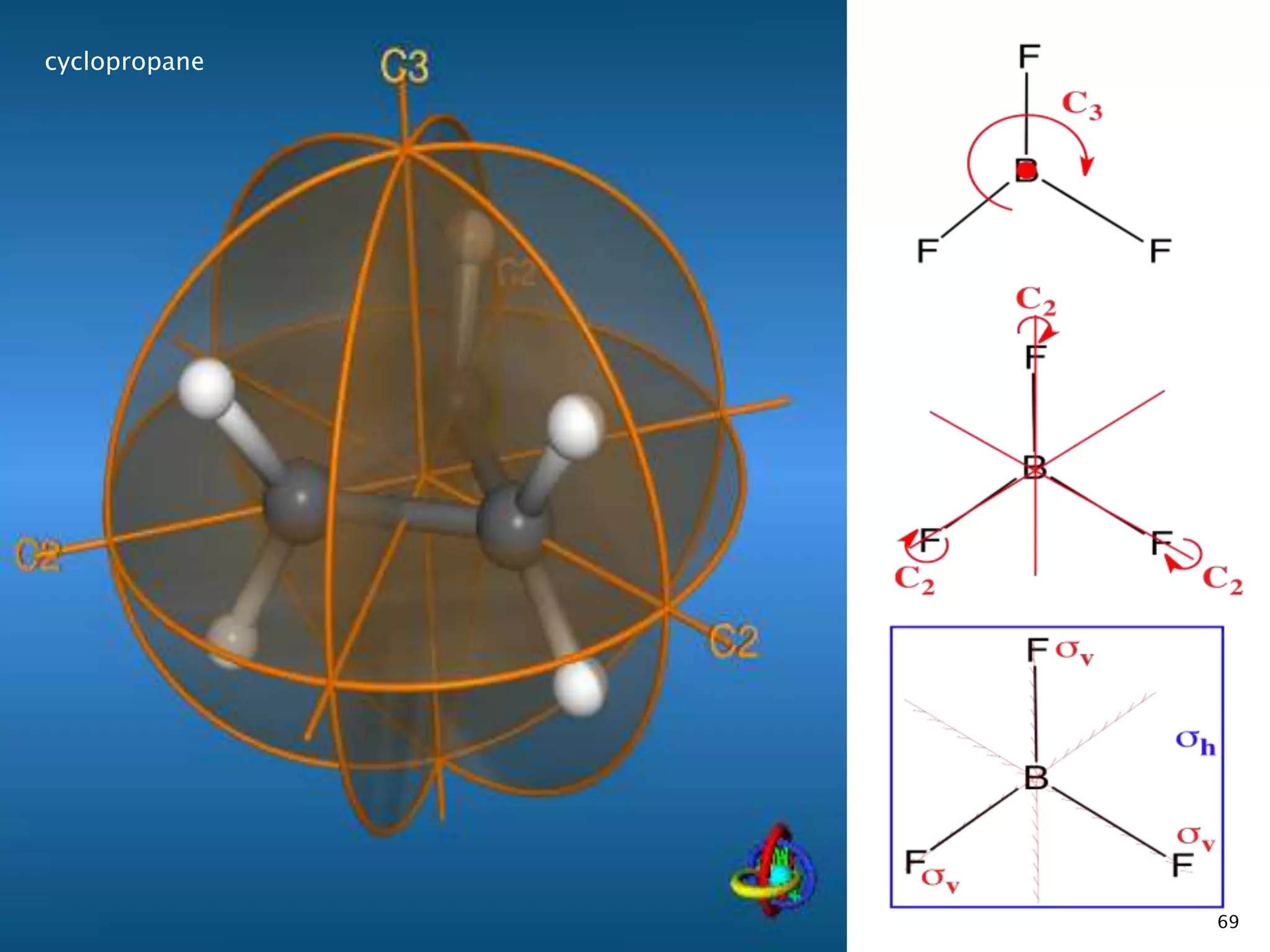
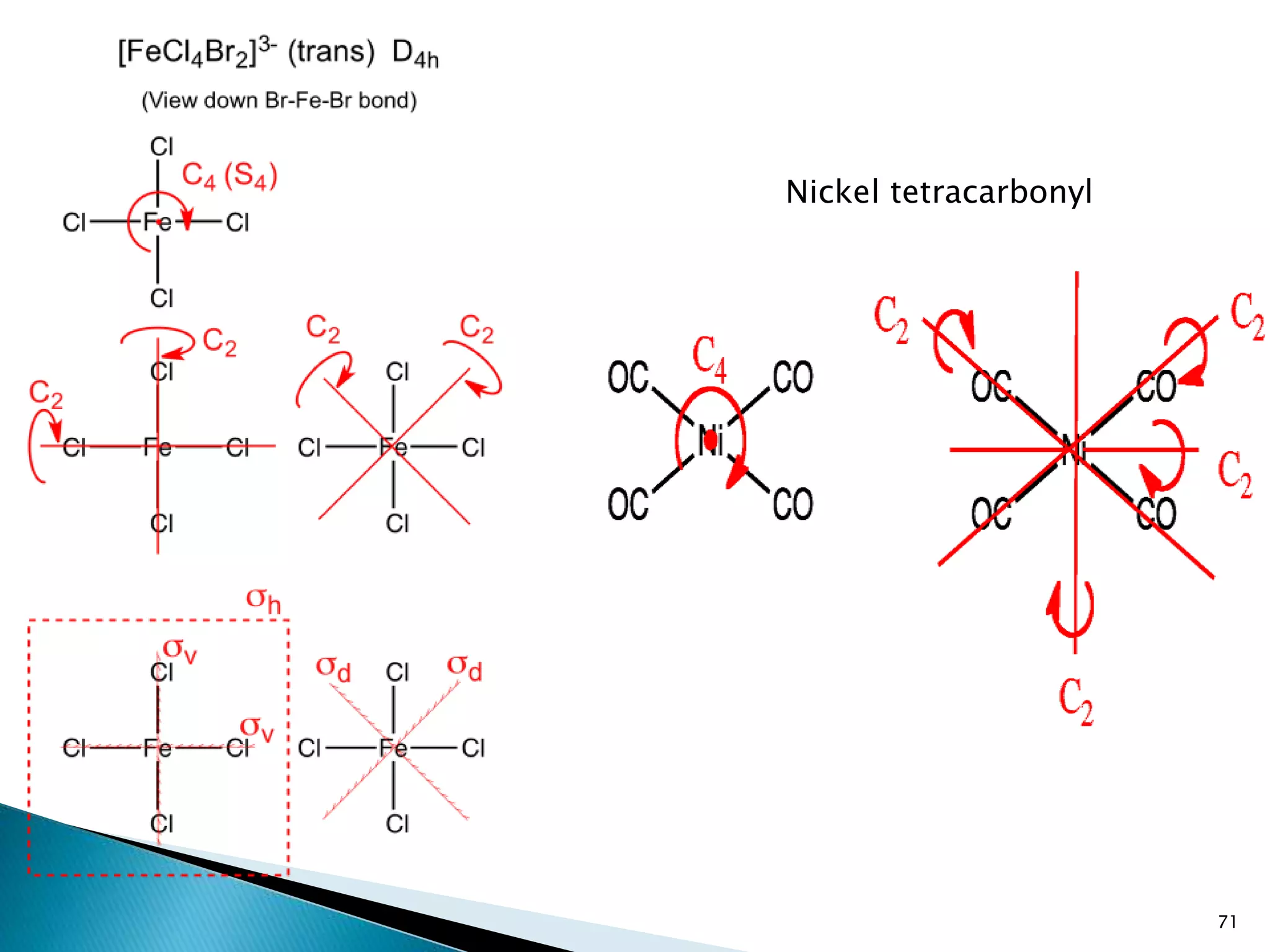
72. 72
[AlCl₄]− Xenon tetrafluoride

73. 73
This point group contains the following symmetry
operations
E the identity operation
C5 4-fold symmetry axis.
5C2 2-fold symmetry axis.
σh horizontal plane
5σv vertical plane
S5 improper axis of symmetry

74. 74

75. 75
This point group contains the following symmetry operations
E the identity operation
C6 6-fold symmetry axis.
6C2 2-fold symmetry axis.
σh horizontal plane
6σv vertical plane
S6 improper axis of symmetry
i inversion

76. 76

77. 77
This point group contains the following symmetry operations
E the identity operation
C ∞ 4-fold symmetry axis.
∞ C2 2-fold symmetry axis.
σh horizontal plane
∞ σv vertical plane
S ∞ improper axis of symmetry
i inversion

78. 78
POSSESS CENTER OF SYMMETRY

79. 79

80. 80
This point group contains the following
symmetry operations
E the identity operation
4C3 3-fold symmetry axis.
3C2 2-fold symmetry axis.
6σd dihedral plane
3S4 improper axis of symmetry
Total: 24 elements

81. 81
METHANE

82. 82
NEOPENTANE

83. 83
This point group contains the following symmetry operations
E the identity operation
3C4 4-fold symmetry axis.
3C2 2-fold symmetry axis.
3σh dihedral plane
3S4 improper axis of symmetry
i inversion
C3 3-fold symmetry axis
S6 improper axis of symmetry
6C2 2-fold symmetry axis.
6σd dihedral plane
TOTAL :48 elements

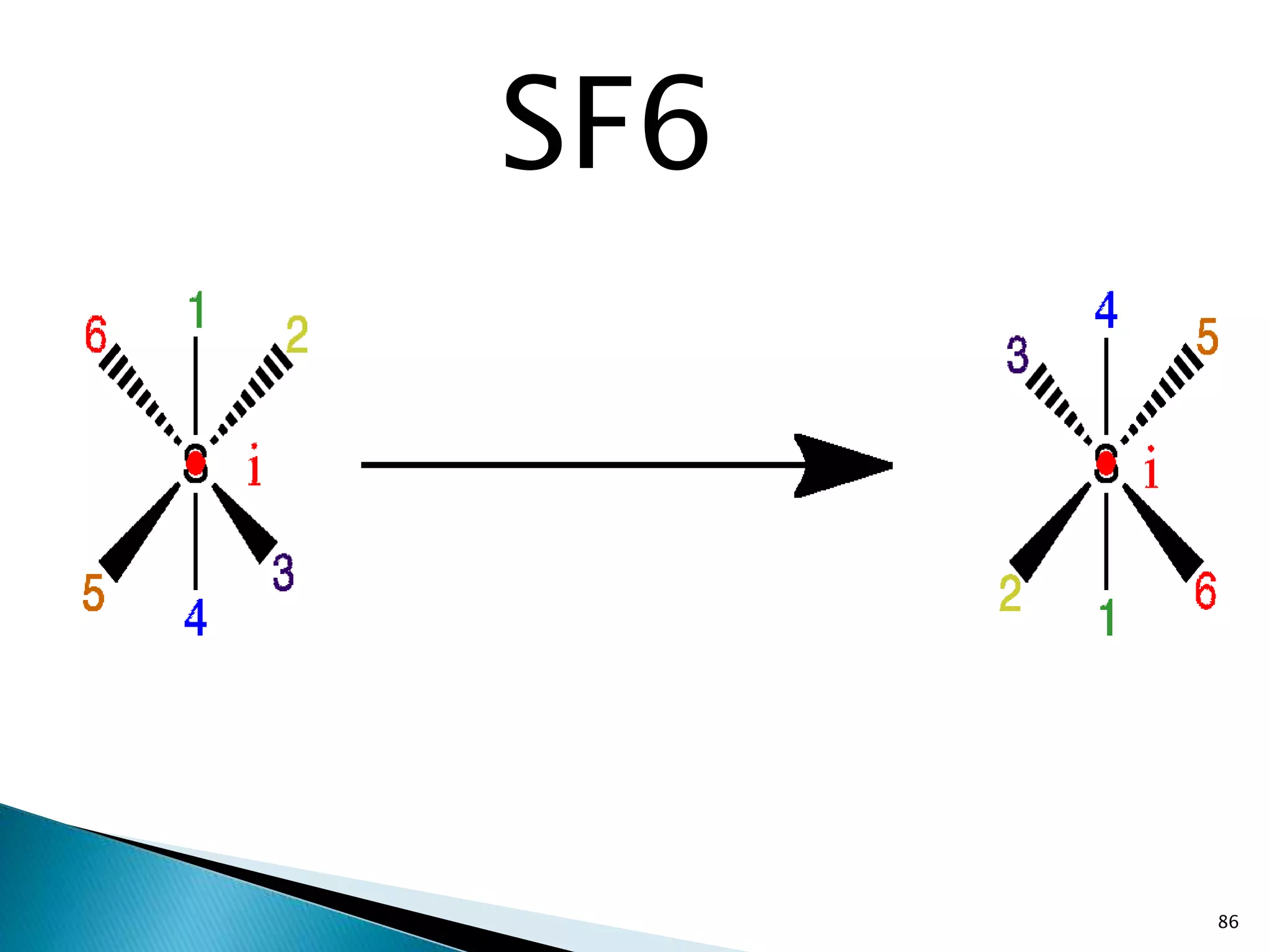
84. 84
Cr(CO)6
[PtCl6]2-

85. 85
PF6- CUBANE

86. 86
SF6

87. 87
This point group contains the following symmetry operations
E the identity operation
20C3 3-fold symmetry axis.
15C2 2-fold symmetry axis.
15σh horizontal plane
20S6 improper axis of symmetry
i inversion
20C3 3-fold symmetry axis
12S10 improper axis of symmetry
12C5 5-fold symmetry axis.
12S10* improper axis of symmetry
TOTAL : 120 elements

88. 88
dodecahedran fullerenes

89. 89